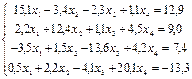Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое моделирование. Решение нелинейных уравненийСтр 1 из 7Следующая ⇒
Решение нелинейных уравнений
Любое нелинейное уравнение можно свести к виду
Существует несколько методов решения этого уравнения, и применение того или иного метода определяется видом функции Если Следствие: Если Это утверждение вытекает из того, что функция
Рис.2
Метод 1/2 деления (метод бисекции, метод дихотомии) Основная идея метода половинного деления основывается на приведенном выше утверждении. Отрезок, содержащий корень
Метод простой итерации В рассмотренных выше методах для решения уравнения (1.1) строилась последовательность приближений, которая сходится к корню уравнения. Такие последовательности называются итерационными. Наряду с методом Ньютона и методом секущих получили широкое распространение и другие методы, в частности метод простой итерации. Чтобы применить метод простой итерации для решения уравнения (1.1), необходимо преобразовать это уравнение к виду
Рис.5 Это приведение к виду, удобному для итераций, можно выполнить разными способами (например Выберем каким-либо образом приближенное значение корня
На рис.5 показана геометрическая интерпретация метода простой итерации. Корень уравнения (1.4) есть абсцисса точки пересечения графиков функций что Сходимость Рассматривая итерационные методы решения нелинейных уравнений, мы оставили в стороне вопрос о сходимости итерационных последовательностей. Ведь вполне может получиться так, что Пусть в некоторой окрестности корня где Замечание. Для практического применения метода простой итерации и выбора начального приближения часто используют условие Пример. Пусть необходимо найти положительный корень уравнения Отсюда легко выводится аналогичное условие сходимости для метода Ньютона. Сравнивая формулы (1.2) и (1.6), можно представить решение уравнения (1.1) методом Ньютона как решение уравнения (1.5) методом простой итерации с функцией
Для реализации итерационных методов приближенного решения нелинейных уравнений остается лишь запрограммировать формулы (1.2), (1.3), (1.4) или (1.6) получения последовательных приближений. Рекомендуется использовать цикл repeat...until, причем выход из цикла осуществить при выполнении условия
Метод Гаусса Рассмотрим систему уравнений N-го порядка:
В матричном виде эта система записывается в виде 1. Прямой ход метода Гаусса: исключая 2. Обратный ход метода Гаусса: последовательно исключаются Для составления программы, реализующей метод Гаусса, удобно пользоваться приведенными ниже формулами. Здесь вводятся вспомогательные матрица C размерности Сначала для прямого хода в цикле для К от 1 до N необходимо вычислять
Затем обратный ход метода позволяет получить решение в виде
Замечание 1. Может случиться так, что во время вычислений встретился ведущий элемент ( Замечание 2. Даже если главный определитель системы ненулевой, ведущий элемент может оказаться равным нулю, что опять приведет к ошибке. Поэтому рекомендуется применять модификацию метода Гаусса - алгоритм с выбором главного элемента. В этом случае на каждом шаге матрица коэффициентов преобразуется так, чтобы на месте ведущего элемента оказывался наибольший по абсолютной величине элемент строки. Кроме гарантии от ошибки применение метода с выбором главного элемента может существенно уменьшить погрешность вычислений. Замечание 3. Количество арифметических действий в методе Гаусса растет с увеличением порядка системы Метод Зейделя Другой итерационный способ решения систем линейных уравнений вида (2.4) носит имя Зейделя, и его можно рассматривать как модификацию метода Якоби. Последовательные приближения строятся здесь по формуле
Отличия двух методов хорошо иллюстрирует следующий пример: Пример. Рассматривая систему трех уравнений с тремя неизвестными, которая приводилась выше, найдем ее решение методом Зейделя, оставляя каждый раз при вычислениях два знака после запятой:
Возьмем в качестве начального приближения
Обратите внимание, что в методе Зейделя при вычислении Приведенное решение показывает, что метод Зейделя быстрее сходится к решению, чем метод Якоби, однако в общем случае это неверно. Дело в том, что эти методы ориентированы на решение разных классов систем: метод Якоби - на системы с матрицами, близкими к диагональным, а метод Зейделя - на системы с матрицами, близкими к нижним треугольным.
Достаточные условия сходимости метода Зейделя формулируются следующей теоремой: Если причем хотя бы для одного Докажем эту теорему для системы двух уравнений с двумя неизвестными: Пусть
для предыдущего шага итерации эта формула имеет вид
Линейная аппроксимация Ставится задача найти коэффициенты аппроксимирующего многочлена, если предположить, что он имеет линейный вид: Эта система может быть записана в виде где Таким образом, вычисляя по этим формулам значения коэффициентов системы и свободных членов, можно найти затем ее решение каким-либо известным методом. Остается лишь запрограммировать формулы (3.7) перед тем, как воспользоваться стандартной процедурой решения систем линейных уравнений, описанной раньше, например. В результате будут найдены значения коэффициентов
Квадратичная аппроксимация Аналогично решается задача нахождения коэффициентов аппроксимирующего многочлена 2-го порядка. В этом случае он имеет вид где Как видно из формул (3.8), полученная система симметрична и хорошо решается методом Гаусса, не требуя выбора главных элементов. Однако для многочленов более высокой степени ( Замечание 1. В том случае, когда m=n, найденный методом наименьших квадратов аппроксимирующий многочлен совпадает с интерполяционным многочленом. При этом минимизируемая функция Замечание 2. Как правило, при использовании метода наименьших квадратов предполагается, что
Численное интегрирование
В прикладных исследованиях часто возникает необходимость вычисления определенных интегралов
Определение: квадратурной формулой называется приближенное равенство вида где
Ниже рассматриваются некоторые широко распространенные простые квадратурные формулы. Все они основаны на геометрических представлениях. Будем интерпретировать интеграл как площадь криволинейной трапеции, ограниченной графиком функции
Рис.7
Разобьем отрезок Формулы прямоугольников Заменим приближенно площадь элементарной криволинейной трапеции площадью прямоугольника, основанием которого является отрезок
Рис.8
Если взять за высоту прямоугольника значение Во втором случае Наконец, если за высоту прямоугольника брать значение функции Названия формул (4.2) и (4.3) следуют из геометрической иллюстрации (рис.8). В соответствии с этим приближенное равенство (4.4) иногда называют формулой центральных прямоугольников. Ниже, когда будут рассматриваться вопросы о точности квадратурных формул, выяснится, что она точнее на порядок по сравнению с (4.2) и (4.3). По этой причине для численного интегрирования гораздо чаще применяют (4.4) и называют ее просто формулой прямоугольников. Для всех трех полученных формул их применение означает приближенную замену площади исходной криволинейной трапеции площадью ступенчатой фигуры, состоящей из элементарных прямоугольников (рис.9 - для формулы центральных прямоугольников).
Рис.9 Формула трапеций Соединив отрезком точки
Эта формула соответствует приближенной замене площади исходной криволинейной трапеции площадью фигуры, ограниченной ломаной линией, проходящей через точки
Рис. 10 Рис. 11
Формула Симпсона (парабол) Если площадь элементарной криволинейной трапеции заменить площадью фигуры, расположенной под параболой, проходящей через точки
Интегрирование полученного выражения на элементарном отрезке приводит к равенству
Таким образом, получена элементарная квадратурная формула Симпсона. Применяя эту формулу и суммируя результаты для всего отрезка интегрирования, выводим составную квадратурную формулу Симпсона:
Замечание 1. Учитывая геометрическую интерпретацию формулы Симпсона, ее иногда называют формулой парабол. Замечание 2. В случае, когда число элементарных отрезков разбиения четно ( Эта формула легко вытекает из (4.6), если при выводе принять Оценка погрешности Итак, полученные формулы (4.2)-(4.7) позволяют приближенно вычислять определенные интегралы. Программирование здесь сводится к тривиальному использованию операторов цикла для вычисления сумм, поэтому нет необходимости приводить здесь тексты программ. Другой важный вопрос - в каких случаях применять ту или иную формулу - связан с погрешностью вычислений. Оценим погрешность выведенных квадратурных формул. Будем использовать обозначение Пусть функция Так как В точности такая же оценка погрешности справедлива и для формулы правых прямоугольников. Ее можно получить, проведя аналогичные выкладки при разложении функции по формуле Тейлора в окрестности точки Подобным же способом оцениваются погрешности других квадратурных формул. Справедливы следующие утверждения (без доказательства):
Пусть функция а для формулы трапеций: Приведенные оценки показывают, что формулы (4.2) и (4.3) имеют лишь первый порядок точности относительно Замечание3. Из оценок (4.9)-(4.11) следует, что формулы прямоугольников и трапеций точны для многочленов первой степени, а формула Симпсона - для многочленов четвертой степени. Замечание4. При вычислении интегралов по приведенным выше квадратурным формулам необходимо учитывать тот фактор, что при увеличении числа узлов возрастает влияние ошибок округления, поэтому для повышения точности рекомендуется не столько увеличивать это число, сколько применять более точную формулу.
Метод Эйлера Простейший дискретный аналог дифференциального уравнения (5.1) представляет собой уравнение Геометрическая интерпретация метода Эйлера проиллюстрирована на рис.12. На каждом шаге вычислений строится касательная к интегральной кривой в точке
Рис. 12 Реализация численного алгоритма на компьютере предполагает построение алгоритма, позволяющего вычислить решение поставленной дискретной задачи Коши. В данном случае (и во всех ниже рассматриваемых случаях) вычисления производятся по явной формуле - значение сеточной функции зависит только от предыдущих значений, и программирование алгоритма не вызовет особых затруднений. Такие методы называют явными. В неявных методах правая часть уравнения может зависеть от Метод Эйлера с уточнением Приближенное решение задачи Коши методом Эйлера характеризуется очень медленной сходимостью (его погрешность убывает пропорционально лишь первой степени Метод приближенного решения задачи Коши по формулам (5.4) относится к методам класса прогноз-коррекция и иногда его называют методом Эйлера-Коши. Геометрическая иллюстрация этого метода представлена на рис.13. Если принять ломаную Эйлера в виде цепочки векторов, то значение сеточной функции по формулам (5.4) можно представить как полусумму двух последующих звеньев-векторов.
Рис.13 Как видно из рисунка, вычисленное значение гораздо находится ближе к графику искомой функции. Метод Эйлера-Коши имеет второй порядок точности, и доказательство этого факта можно найти в [1].
Методы Рунге-Кутты Наиболее популярными среди классических явных одношаговых методов являются методы Рунге-Кутты. Рассмотренные выше методы можно рассматривать как частные случаи этого класса методов. Самым известным из методов Рунге-Кутты является метод четвертого порядка точности. Вычисления на каждом шаге здесь проводятся последовательно в четыре этапа. Сначала вычисляются вспомогательные коэффициенты, а затем они подставляются в основную формулу: Этот метод весьма прост и, как показывает практика, довольно эффективен в обычных расчетах. Литература
Приложение: Варианты контрольных работ. Вариант № 1
1. Методом половинного деления и методом хорд определить один из корней уравнения 2. Методом Гаусса найти решение системы уравнений: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами трапеций и Симпсона вычислить интеграл и сделать проверку: 5. Используя метод Эйлера 1ого порядка, составить таблицу решения дифференциального уравнения
Вариант № 2
1. Методом половинного деления и методом касательных определить один из корней уравнения 2. Методом простых итераций найти решение системы уравнений с точностью e=0,00001: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
4. Методами модиф. прямоугольников и трапеций вычислить интеграл и сделать проверку: 5. Используя метод Эйлера-Коши, составить таблицу решения дифференциального уравнения
Вариант № 3
1. Методом половинного деления и методом простых итераций определить один из корней уравнения 2. Методом Зейделя найти решение системы уравнений с точностью e=0,00001: 3. Подобрать по принципу наименьших квадратов для заданных значений X и Y квадратичную функцию:
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.31.77 (0.168 с.) |
 (1.1)
(1.1)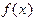 . При рассмотрении различных методов воспользуемся практически очевидным утверждением:
. При рассмотрении различных методов воспользуемся практически очевидным утверждением: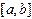 ;
;  и
и 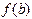 (значения функции на концах отрезка) противоположного знака, то существует
(значения функции на концах отрезка) противоположного знака, то существует  , такой, что
, такой, что  , то есть
, то есть 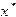 - корень уравнения (1.1).
- корень уравнения (1.1).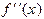 не меняет знак на отрезке
не меняет знак на отрезке 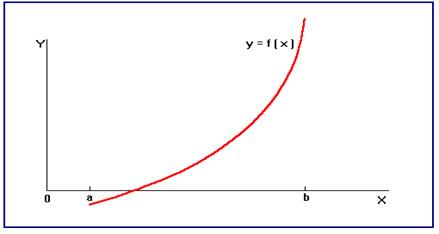
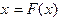 (1.5)
(1.5)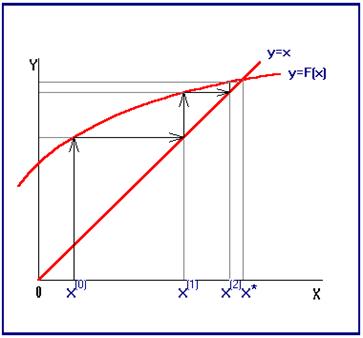
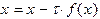 , где
, где  - действительное число).
- действительное число). и подставим его в правую часть уравнения (1.5). Получим значение
и подставим его в правую часть уравнения (1.5). Получим значение 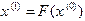 . Подставляя затем
. Подставляя затем 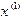 в правую часть уравнения (1.5), получим
в правую часть уравнения (1.5), получим 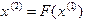 . Продолжая описанные действия таким образом и дальше, находим последовательность приближений по формуле
. Продолжая описанные действия таким образом и дальше, находим последовательность приближений по формуле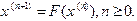 (1.6)
(1.6)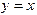 и
и 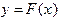 . Пусть
. Пусть 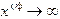 при
при 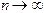 . При реализации алгоритма на компьютере это приведет к типичной ошибке (переполнение с плавающей точкой) и программному прерыванию. Для выяснения условий сходимости служит следующая теорема:
. При реализации алгоритма на компьютере это приведет к типичной ошибке (переполнение с плавающей точкой) и программному прерыванию. Для выяснения условий сходимости служит следующая теорема: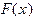 дифференцируема и удовлетворяет неравенству
дифференцируема и удовлетворяет неравенству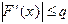 , (1.7)
, (1.7)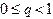 - некоторая постоянная величина. Тогда независимо от выбора начального приближения из указанной окрестности корня итерационная последовательность не выходит из этой окрестности, метод (1.6) сходится со скоростью геометрической прогрессии, и справедлива следующая оценка погрешности:
- некоторая постоянная величина. Тогда независимо от выбора начального приближения из указанной окрестности корня итерационная последовательность не выходит из этой окрестности, метод (1.6) сходится со скоростью геометрической прогрессии, и справедлива следующая оценка погрешности: 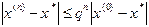 .
.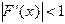 .
. . Как видно, производная правой части этого уравнения больше единицы для положительных
. Как видно, производная правой части этого уравнения больше единицы для положительных 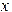 , и метод простой итерации приведет к расходящейся последовательности. Тогда исходное уравнение необходимо преобразовать так, чтобы удовлетворить условию сходимости. В данном случае, например, можно представить его в виде
, и метод простой итерации приведет к расходящейся последовательности. Тогда исходное уравнение необходимо преобразовать так, чтобы удовлетворить условию сходимости. В данном случае, например, можно представить его в виде 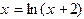 .
.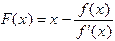 . Дифференцируя эту функцию, получим, что
. Дифференцируя эту функцию, получим, что 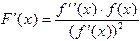 . Таким образом, условие сходимости для метода Ньютона выглядит как
. Таким образом, условие сходимости для метода Ньютона выглядит как 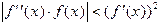 .
.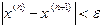 , где
, где 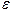 -заданная точность.
-заданная точность.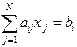 , где
, где  . (2.1)
. (2.1) . Метод Гаусса изучался в курсе высшей математики, и напомним, что основная идея метода заключается в следующем.
. Метод Гаусса изучался в курсе высшей математики, и напомним, что основная идея метода заключается в следующем.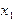 из всех уравнений, кроме первого, получаем в первом столбце коэффициентов матрицы нули во всех строках, кроме первой. Затем исключаем
из всех уравнений, кроме первого, получаем в первом столбце коэффициентов матрицы нули во всех строках, кроме первой. Затем исключаем  из всех уравнений, кроме первого и второго. Продолжая эти действия дальше, исключаем
из всех уравнений, кроме первого и второго. Продолжая эти действия дальше, исключаем  ,
,  ,... и приходим, наконец, к матрице треугольного вида.
,... и приходим, наконец, к матрице треугольного вида. из (N-1)-го уравнения,
из (N-1)-го уравнения, 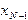 из (N-2)-го уравнения и т.д. Это приводит к диагональному виду матрицы коэффициентов и, соответственно к решению задачи.
из (N-2)-го уравнения и т.д. Это приводит к диагональному виду матрицы коэффициентов и, соответственно к решению задачи.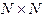 и вектор Y, состоящий из N элементов.
и вектор Y, состоящий из N элементов. (2.2)
(2.2)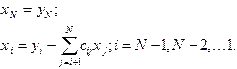 (2.3)
(2.3) ), равный нулю. Это приведет к ошибке и программному прерыванию (деление на нуль). Такое бывает, например, в том случае, когда исходная система вырождена, то есть ее главный определитель равен нулю, и тогда либо решения нет, либо существует бесконечное множество решений.
), равный нулю. Это приведет к ошибке и программному прерыванию (деление на нуль). Такое бывает, например, в том случае, когда исходная система вырождена, то есть ее главный определитель равен нулю, и тогда либо решения нет, либо существует бесконечное множество решений. .
. , где
, где  . (2.7)
. (2.7) . Тогда
. Тогда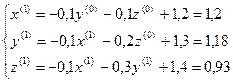 ,
, 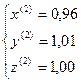 ,
,  ,...
,... используется уже найденное на этом шаге
используется уже найденное на этом шаге 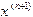 , а при вычислении
, а при вычислении  используются
используются  для
для 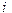 неравенство строгое, то итерационная последовательность (2.7) сходится к решению системы (2.1) при любом начальном приближении.
неравенство строгое, то итерационная последовательность (2.7) сходится к решению системы (2.1) при любом начальном приближении.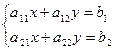
 Приведем эту систему к виду, удобному для итераций:
Приведем эту систему к виду, удобному для итераций: 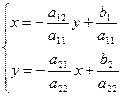 , тогда
, тогда 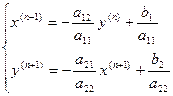 . Подставляя
. Подставляя 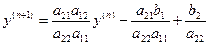 (*)
(*) (**) Вычтем (**) из (*) и возьмем разность по абсолютной величине:
(**) Вычтем (**) из (*) и возьмем разность по абсолютной величине: 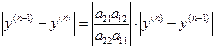 . Аналогично можно получить, что
. Аналогично можно получить, что 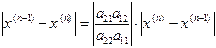 . Известно, что итерационная схема сходится, если
. Известно, что итерационная схема сходится, если 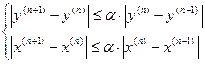 при
при  . Это означает, что при выполнении условий теоремы
. Это означает, что при выполнении условий теоремы 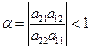 и схема сходится, что и требовалось доказать.
и схема сходится, что и требовалось доказать.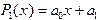 . Тогда минимизируемая функция - функция двух переменных
. Тогда минимизируемая функция - функция двух переменных  , и для нахождения наилучших по принципу наименьших квадратов коэффициентов получаем систему двух линейных алгебраических уравнений с двумя неизвестными:
, и для нахождения наилучших по принципу наименьших квадратов коэффициентов получаем систему двух линейных алгебраических уравнений с двумя неизвестными: . (3.6)
. (3.6) ,
, ,
, 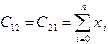 ,
,  ,
, 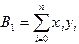 ,
, 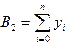 . (3.7)
. (3.7)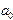 и
и 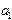 , а график искомой функции будет представлять собой прямую и может выглядеть, например, как на рис.6,в.
, а график искомой функции будет представлять собой прямую и может выглядеть, например, как на рис.6,в.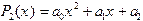 и график представляет собой параболу. Минимизируемая функция - функция трех переменных
и график представляет собой параболу. Минимизируемая функция - функция трех переменных 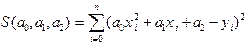 . Повторяя те же выкладки, что и в предыдущем разделе, можно прийти к системе трех уравнений с тремя неизвестными (проделайте их самостоятельно):
. Повторяя те же выкладки, что и в предыдущем разделе, можно прийти к системе трех уравнений с тремя неизвестными (проделайте их самостоятельно):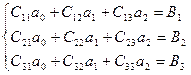 ,
, ,
,  ,
, 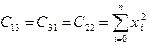 ,
, 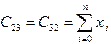 ,
,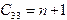 ,
, 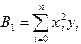 ,
,  ,
,  . (3.8)
. (3.8)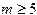 ) использование такого метода не рекомендуется, так как вычисленные на ЭВМ параметры могут оказаться полностью искаженными ошибками округления.
) использование такого метода не рекомендуется, так как вычисленные на ЭВМ параметры могут оказаться полностью искаженными ошибками округления.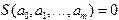 , и значения многочлена в узловых точках совпадают с табличными значениями.
, и значения многочлена в узловых точках совпадают с табличными значениями. . В этом случае метод обладает некоторыми сглаживающими свойствами.
. В этом случае метод обладает некоторыми сглаживающими свойствами.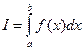 . К сожалению, в подавляющем большинстве случаев получить значение такого интеграла известными аналитическими методами не удается. Например, интеграл
. К сожалению, в подавляющем большинстве случаев получить значение такого интеграла известными аналитическими методами не удается. Например, интеграл 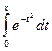 широко используется при исследовании процессов теплообмена и диффузии, в статистической физике и теории вероятностей. Однако его значение не может быть выражено в виде конечной комбинации элементарных функций. В других случаях окончательный результат выражается чрезмерно громоздкой формулой, неудобной для дальнейших вычислений. Иногда подынтегральная функция задана таблично, и точное значение интеграла получить невозможно. Тогда применяют специальные методы численного интегрирования.
широко используется при исследовании процессов теплообмена и диффузии, в статистической физике и теории вероятностей. Однако его значение не может быть выражено в виде конечной комбинации элементарных функций. В других случаях окончательный результат выражается чрезмерно громоздкой формулой, неудобной для дальнейших вычислений. Иногда подынтегральная функция задана таблично, и точное значение интеграла получить невозможно. Тогда применяют специальные методы численного интегрирования. , (4.1)
, (4.1) - некоторые точки из отрезка
- некоторые точки из отрезка  - числовые коэффициенты, называемые весами квадратурной формулы. Величина
- числовые коэффициенты, называемые весами квадратурной формулы. Величина 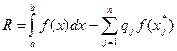 называется погрешностью (или остаточным членом) квадратурной формулы.
называется погрешностью (или остаточным членом) квадратурной формулы.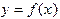 (при
(при 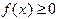 ), осью абсцисс и прямыми
), осью абсцисс и прямыми 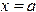 и
и  (рис.7).
(рис.7).
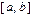 на элементарные отрезки
на элементарные отрезки  точками
точками 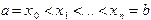 . Интеграл разобьется при этом на сумму элементарных интегралов
. Интеграл разобьется при этом на сумму элементарных интегралов 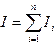 , где
, где  , что соответствует разбиению площади исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций (рис.7). Введем обозначения:
, что соответствует разбиению площади исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций (рис.7). Введем обозначения: 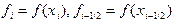 , где
, где 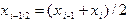 - середина элементарного отрезка. Для простоты шаг
- середина элементарного отрезка. Для простоты шаг 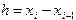 будем считать постоянным (
будем считать постоянным ( ).
). , а высота равна либо
, а высота равна либо  (рис.8,а), либо
(рис.8,а), либо  (рис.8,б), либо
(рис.8,б), либо  (рис.8,в).
(рис.8,в).
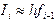 , тогда, суммируя все элементарные площади, получаем квадратурную формулу левых прямоугольников:
, тогда, суммируя все элементарные площади, получаем квадратурную формулу левых прямоугольников: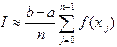 . (4.2)
. (4.2) , и тогда приходим к квадратурной формуле правых прямоугольников:
, и тогда приходим к квадратурной формуле правых прямоугольников: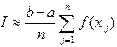 . (4.3)
. (4.3)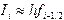 , а составная формула выглядит как
, а составная формула выглядит как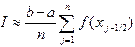 . (4.4)
. (4.4)
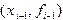 и
и  на графике функции
на графике функции 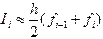 . Пользуясь этой формулой для каждой элементарной трапеции и суммируя их площади, получим составную квадратурную формулу трапеций:
. Пользуясь этой формулой для каждой элементарной трапеции и суммируя их площади, получим составную квадратурную формулу трапеций: . (4.5)
. (4.5)

 и
и  . Здесь
. Здесь 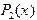 - интерполяционный многочлен 2-й степени с узлами
- интерполяционный многочлен 2-й степени с узлами 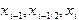 . На рис.11 показана такая парабола, а график функции
. На рис.11 показана такая парабола, а график функции 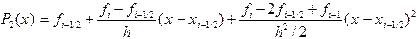 .
.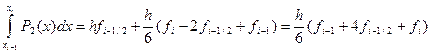 .
.  (4.6)
(4.6)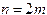 ), в формуле Симпсона можно использовать узлы лишь с целыми индексами:
), в формуле Симпсона можно использовать узлы лишь с целыми индексами: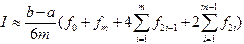 (4.7)
(4.7)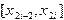 за элементарный отрезок длины
за элементарный отрезок длины  .
.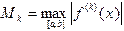 - максимальное значение производной
- максимальное значение производной 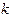 -го порядка от подынтегральной функции на отрезке
-го порядка от подынтегральной функции на отрезке  .
. , где
, где  , имеем
, имеем 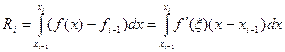 , и тогда
, и тогда .
. , то, заменяя
, то, заменяя 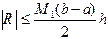 . (4.8)
. (4.8)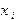 .
.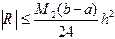 , (4.9)
, (4.9)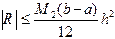 . (4.10)
. (4.10)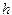 , поэтому они используются крайне редко. Предпочтительнее использование формул (4.4) и (4.5), которые имеют второй порядок точности. Однако вычисление интегралов по формуле Симпсона дает четвертый порядок точности относительно
, поэтому они используются крайне редко. Предпочтительнее использование формул (4.4) и (4.5), которые имеют второй порядок точности. Однако вычисление интегралов по формуле Симпсона дает четвертый порядок точности относительно  . (4.11)
. (4.11) ,
,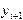 осуществляется здесь по формуле
осуществляется здесь по формуле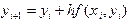 . (5.3)
. (5.3)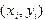 , и за
, и за 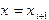 . В результате неизвестная интегральная кривая заменяется ломаной линией, называемой ломаной Эйлера.
. В результате неизвестная интегральная кривая заменяется ломаной линией, называемой ломаной Эйлера.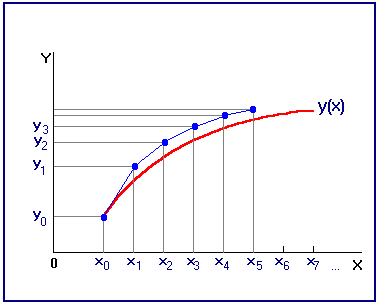
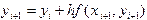 .
.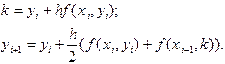 (5.4)
(5.4)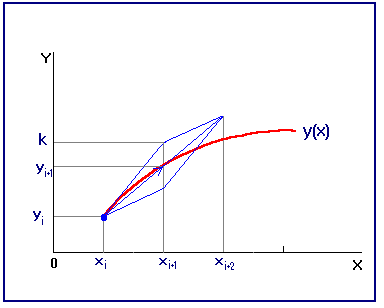
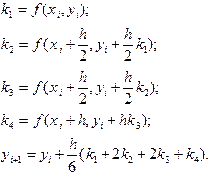 (5.5)
(5.5)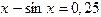 с точностью до e=0,0001
с точностью до e=0,0001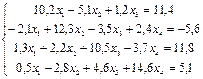
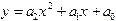
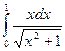
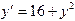 с начальным условием
с начальным условием 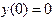 и шагом
и шагом 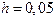 на отрезке
на отрезке 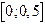
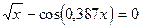 с точностью до e=0,0001
с точностью до e=0,0001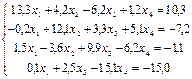
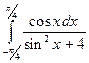
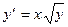 с начальным условием
с начальным условием 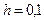 на отрезке
на отрезке 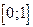
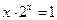 с точностью до e=0,0001
с точностью до e=0,0001