
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Ньютона ( метод касательных )Содержание книги Поиск на нашем сайте
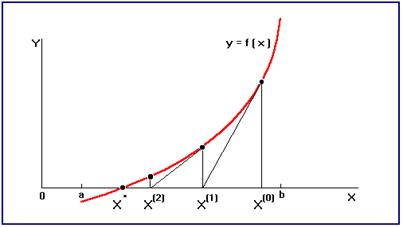
Метод Ньютона является одним из наиболее эффективных методов решения самых разных нелинейных задач. Выведем расчетную формулу метода решения уравнения (1.1) из простых геометрических соображений. Соответствующая иллюстрация приведена на рис. 3.
Рис.3 Пусть Тогда, полагая в этой формуле
Благодаря такой геометрической интерпретации метод Ньютона часто называют методом касательных. 1.3. Метод секущих (метод хорд) При решении уравнения (1.1) методом Ньютона иногда возникают сложности при взятии производной функции в формуле (1.2). Это случается, например, когда функция
Метод называется двухшаговым, так как требуется не одно, а два начальных приближения: Здесь c равно либо a, либо b, в зависимости от знака функции
Рис.4 В качестве начального приближения Метод простой итерации В рассмотренных выше методах для решения уравнения (1.1) строилась последовательность приближений, которая сходится к корню уравнения. Такие последовательности называются итерационными. Наряду с методом Ньютона и методом секущих получили широкое распространение и другие методы, в частности метод простой итерации. Чтобы применить метод простой итерации для решения уравнения (1.1), необходимо преобразовать это уравнение к виду
Рис.5 Это приведение к виду, удобному для итераций, можно выполнить разными способами (например Выберем каким-либо образом приближенное значение корня На рис.5 показана геометрическая интерпретация метода простой итерации. Корень уравнения (1.4) есть абсцисса точки пересечения графиков функций что Сходимость Рассматривая итерационные методы решения нелинейных уравнений, мы оставили в стороне вопрос о сходимости итерационных последовательностей. Ведь вполне может получиться так, что Пусть в некоторой окрестности корня где Замечание. Для практического применения метода простой итерации и выбора начального приближения часто используют условие Пример. Пусть необходимо найти положительный корень уравнения Отсюда легко выводится аналогичное условие сходимости для метода Ньютона. Сравнивая формулы (1.2) и (1.6), можно представить решение уравнения (1.1) методом Ньютона как решение уравнения (1.5) методом простой итерации с функцией
Для реализации итерационных методов приближенного решения нелинейных уравнений остается лишь запрограммировать формулы (1.2), (1.3), (1.4) или (1.6) получения последовательных приближений. Рекомендуется использовать цикл repeat...until, причем выход из цикла осуществить при выполнении условия
|
||||
|
Последнее изменение этой страницы: 2021-05-12; просмотров: 164; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.44.145 (0.008 с.) |

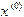 - заданное начальное приближение к корню
- заданное начальное приближение к корню 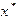 . В точке с координатами
. В точке с координатами 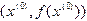 проведем касательную к графику функции
проведем касательную к графику функции 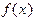 и за новое приближение
и за новое приближение 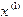 примем абсциссу точки пересечения этой касательной с осью Ox. Аналогично, за приближение
примем абсциссу точки пересечения этой касательной с осью Ox. Аналогично, за приближение 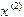 примем абсциссу точки пересечения с осью Ox касательной, проведенной к графику в точке с координатами
примем абсциссу точки пересечения с осью Ox касательной, проведенной к графику в точке с координатами 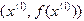 . Продолжая этот процесс далее, получим последовательность приближений к корню
. Продолжая этот процесс далее, получим последовательность приближений к корню 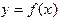 в точке
в точке 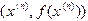 , имеет вид
, имеет вид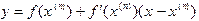
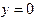 , найдем абсциссу точки пересечения касательной с осью Ox и, соответственно, выражение для следующего приближения:
, найдем абсциссу точки пересечения касательной с осью Ox и, соответственно, выражение для следующего приближения: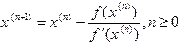 (1.2)
(1.2)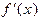 приближенным выражением
приближенным выражением 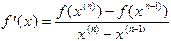 , то получится расчетная формула для двухшагового метода секущих:
, то получится расчетная формула для двухшагового метода секущих: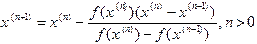 . (1.3)
. (1.3)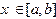 , функция
, функция 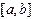 значения разных знаков. Тогда, как мы знаем, существует корень
значения разных знаков. Тогда, как мы знаем, существует корень  уравнения (1.1), причем он единственный в случае, когда
уравнения (1.1), причем он единственный в случае, когда 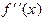 не меняет знак. Это обстоятельство объясняет применение одношагового метод секущих:
не меняет знак. Это обстоятельство объясняет применение одношагового метод секущих: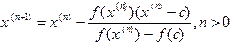 . (1.4)
. (1.4) и знака ее второй производной (выбирается тот конец отрезка, где знаки
и знака ее второй производной (выбирается тот конец отрезка, где знаки 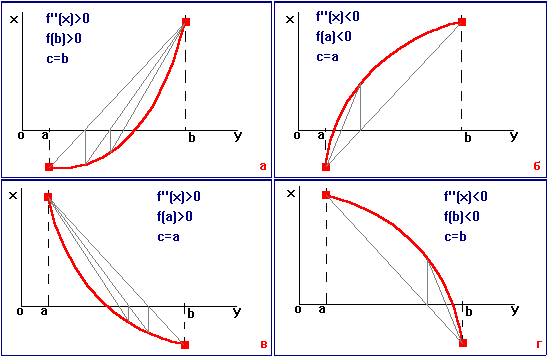
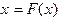 (1.5)
(1.5)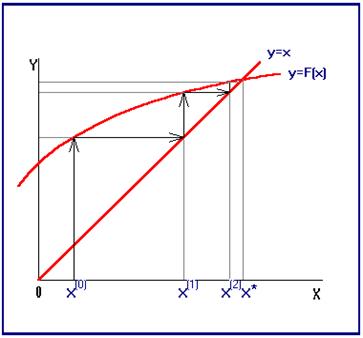
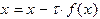 , где
, где 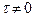 - действительное число).
- действительное число).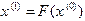 . Подставляя затем
. Подставляя затем 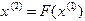 . Продолжая описанные действия таким образом и дальше, находим последовательность приближений по формуле
. Продолжая описанные действия таким образом и дальше, находим последовательность приближений по формуле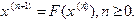 (1.6)
(1.6)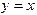 и
и 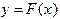 . Пусть
. Пусть 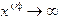 при
при 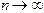 . При реализации алгоритма на компьютере это приведет к типичной ошибке (переполнение с плавающей точкой) и программному прерыванию. Для выяснения условий сходимости служит следующая теорема:
. При реализации алгоритма на компьютере это приведет к типичной ошибке (переполнение с плавающей точкой) и программному прерыванию. Для выяснения условий сходимости служит следующая теорема: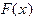 дифференцируема и удовлетворяет неравенству
дифференцируема и удовлетворяет неравенству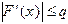 , (1.7)
, (1.7)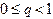 - некоторая постоянная величина. Тогда независимо от выбора начального приближения из указанной окрестности корня итерационная последовательность не выходит из этой окрестности, метод (1.6) сходится со скоростью геометрической прогрессии, и справедлива следующая оценка погрешности:
- некоторая постоянная величина. Тогда независимо от выбора начального приближения из указанной окрестности корня итерационная последовательность не выходит из этой окрестности, метод (1.6) сходится со скоростью геометрической прогрессии, и справедлива следующая оценка погрешности: 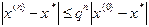 .
.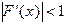 .
. . Как видно, производная правой части этого уравнения больше единицы для положительных
. Как видно, производная правой части этого уравнения больше единицы для положительных 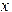 , и метод простой итерации приведет к расходящейся последовательности. Тогда исходное уравнение необходимо преобразовать так, чтобы удовлетворить условию сходимости. В данном случае, например, можно представить его в виде
, и метод простой итерации приведет к расходящейся последовательности. Тогда исходное уравнение необходимо преобразовать так, чтобы удовлетворить условию сходимости. В данном случае, например, можно представить его в виде 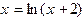 .
.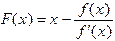 . Дифференцируя эту функцию, получим, что
. Дифференцируя эту функцию, получим, что 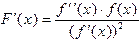 . Таким образом, условие сходимости для метода Ньютона выглядит как
. Таким образом, условие сходимости для метода Ньютона выглядит как 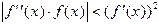 .
.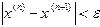 , где
, где 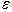 -заданная точность.
-заданная точность.


