Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов измеренийСодержание книги
Поиск на нашем сайте
1. Определить средние значения углов и времени по следующим формулам: где t - среднее значение продолжительности столкновения, 2. При помощи мерной ленты, определить длину подвески шаров в виде 3. По формулам (3.5) и (3.7), (3.8) или 10 определить скорости 4. На аналитических весах измерить массы 5. По формулам (3.4) и (3.6) определить импульс шаров до и после столкновения. 6. Сравнить значения импульсов шаров 7. Определить погрешность по формуле 8. Определить коэффициент восстановления энергии
9. Оценить среднюю силу удара и ускорение
10. Полученные результаты проанализировать и сделать выводы.
Таблица 3.1 – Экспериментальные данные
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Импульс. 2. Закон сохранения импульса и энергии. 3. Столкновения, законы сохранения при столкновениях. 4. Упругие и неупругие столкновения. 5. Почему явление механического удара целесообразно изучать с помощью законов сохранение, чем с помощью законов динамики? 6. Что такое степень упругости kэ удара?
ЛИТЕРАТУРA:[1, с.106-110], [2, с.60-69], [3, с.73-75], [4, с.53-60] Лабораторная работа №1.4
Цель работы: определение частоты переменного тока. Оборудование: струна с электромагнитным возбуждением, набор грузов известной массы.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Упругие волны Волновые процессы. Продольные и поперечные волны Колебания, возбужденные в какой-либо точке среды (твердой, жидкой или газообразной), распространяется в ней с конечной скоростью, зависящей от свойств среды, передаваясь от одной точки среды к другой. Чем дальше расположена частица среды от источника колебаний, тем позднее она начнет колебаться. При изучении распространения колебаний не учитывается дискретное (молекулярное) строение среды и среда рассматривается как сплошная, т.е. непрерывно распределенная в пространстве и обладающая упругими свойствами. Процесс распространения колебаний в сплошной среде, периодический во времени и пространстве, называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн независимо от их природы является перенос энергии без переноса вещества.
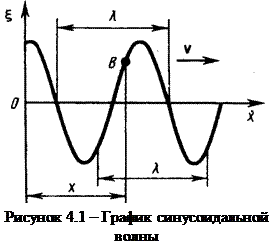
Продольные волны могут распространяться в средах, в которых возникает упругие силы при деформациях сжатия и растяжения, т.е. твердых, жидких и газообразных телах. Поперечные волны могут распространяться в среде, в которой возникают упругие силы при деформации сдвига, т.е. фактически только в твердых телах, в жидкостях и газах возникают только продольные волны, а в твердых телах - как продольные, так и поперечные. Упругая волна называется синусоидальной (или гармонической), если соответствующие ей колебания частиц среды являются гармоническими. На рис. 4.1 представлена синусоидальная поперечная волна, распространяющаяся со скоростью v вдоль оси x т.е. приведена зависимость между смещением Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длинной волны или учитывая, что
Геометрическое место точек, до которых доходят колебания моменту времени t, называется волновым фронтом. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. В принципе волновые поверхности могут быть любой формы, а в простейшем случае они представляют собой совокупность плоскостей, параллельных друг другу, или совокупность концентрических сфер. Соответственно волна называется плоской или сферической.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 71; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.251 (0.008 с.) |

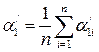 (3.11)
(3.11)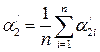 (3.12)
(3.12)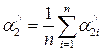 (3.13)
(3.13)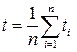 (3.14)
(3.14)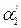 ,
, 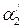 ,
, 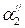 – средние значения угловых расстояний после столкновения шаров;
– средние значения угловых расстояний после столкновения шаров;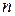 – количество заполненных измерений,
– количество заполненных измерений, 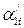 ,
, 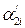 ,
, 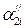 – значения, полученное в і -м замере.
– значения, полученное в і -м замере.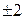 мм.
мм.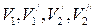 шаров до и после столкновения.
шаров до и после столкновения.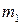 и
и 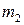 шаров вместе с
шаров вместе с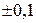 г.
г.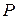 и
и 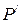 до и после столкновения.
до и после столкновения.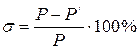
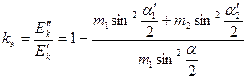
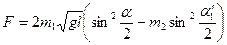
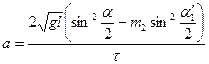
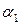
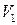
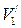
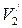
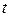
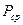
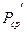
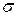
 Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлении распространения волн.
Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлении распространения волн.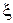 (кси) частиц среды, участвующих в волновом процессе и расстояния х этих частиц (например, частицы В,) от источника колебаний 0 для какого-то фиксированного момента времени t. Приведенный график функции
(кси) частиц среды, участвующих в волновом процессе и расстояния х этих частиц (например, частицы В,) от источника колебаний 0 для какого-то фиксированного момента времени t. Приведенный график функции 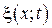 похож на график гармонического колебания, но они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний - зависимость смещения данной частицы от времени.
похож на график гармонического колебания, но они различны по существу. График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени, а график колебаний - зависимость смещения данной частицы от времени.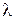 (рис. 4.1). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е.
(рис. 4.1). Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебания за период, т. е.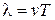 (4.1)
(4.1)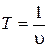 , где
, где 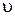 – частота колебаний
– частота колебаний