
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обработка результатов косвенных измеренийСодержание книги
Поиск на нашем сайте
При косвенных измерениях интересующая экспериментатора величина А находится по некоторой формуле где В качестве наилучшего приближения к истинному значению выбирается среднее арифметическое (если прямые измерения выполнялись многократно): Погрешность Значение частных производных берутся в точках а) Пусть (абсолютные погрешности складываются квадратично). б) Пусть Так как (относительные погрешности складываются квадратично). В таблице 2 приведены наиболее часто встречающиеся случаи использования формулы (21).
Таблица 2 – Погрешности косвенных величин
Многие расчетные формулы могут быть сведены к формулам таблицы 2. Пусть, например, Тогда
1.6 Обработка графической информации (метод наименьших квадратов)
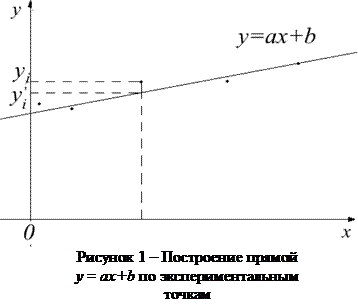
Однако, из-за наличия погрешностей измерения, а в некоторых случаях из-за статического характера исследуемых зависимостей экспериментальные точки не ложатся на теоретическую прямую(см. рисунок 1).
Возникает следующая задача: по экспериментальным точкам провести прямую наилучшим образом, т.е. проходящую по возможности ближе ко всем точкам. В случае числа экспериментальных точек Пусть имеется набор n экспериментальных точек Тогда упомянутая сумма определяется выражением Коэффициенты или Решение системы (25) дает следующие формулы для определения После того как коэффициенты a и b найдены, зависимость Здесь
В заключение приведем формулу метода наименьших квадратов в случае более простой теоретической зависимости:
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 96; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.250.65 (0.009 с.) |

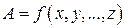 , (19)
, (19)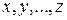 . – результаты прямых измерений.
. – результаты прямых измерений.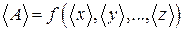 . (20)
. (20)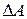 определяется из погрешностей прямых измерений по формуле:
определяется из погрешностей прямых измерений по формуле: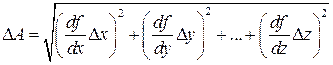 (21)
(21)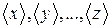 . Формула (21) является общей. В частных случаях она упрощается.
. Формула (21) является общей. В частных случаях она упрощается.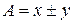 . Тогда
. Тогда 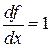 ,
, 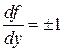 и
и 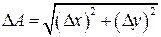
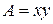 . Тогда
. Тогда 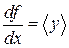 ,
, 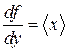 и
и 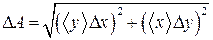 .
.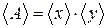 , то
, то 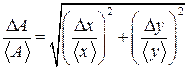
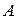
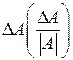
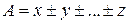
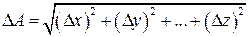
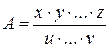
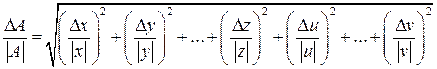
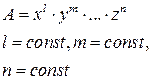
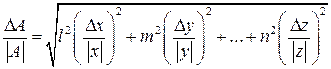
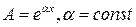
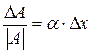
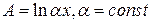
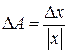
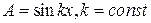
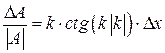
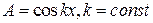
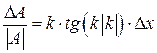
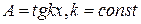
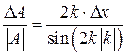
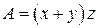 . Положим
. Положим 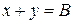 .
.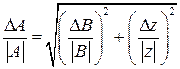 , но
, но 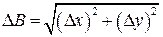 , если
, если 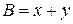 . Окончательно получаем:
. Окончательно получаем: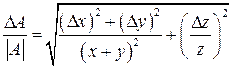 .
. Очень часто цель эксперимента заключается в том, чтобы из опыта найти неизвестный параметр в известной формуле. Так, например, пройденный путь при равноускоренном движении без начальной скорости описывается формулой
Очень часто цель эксперимента заключается в том, чтобы из опыта найти неизвестный параметр в известной формуле. Так, например, пройденный путь при равноускоренном движении без начальной скорости описывается формулой 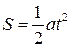 (известна зависимость S от t, требуется определить a); зависимость сопротивления чистого полупроводника от температуры вычисляется по формуле
(известна зависимость S от t, требуется определить a); зависимость сопротивления чистого полупроводника от температуры вычисляется по формуле 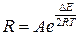 (известна зависимость R от Т, требуется определить ширину запрещённой зоны
(известна зависимость R от Т, требуется определить ширину запрещённой зоны 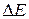 и параметр А). Обе приведенные зависимости являются нелинейными, но, если в первом случае строить график S от
и параметр А). Обе приведенные зависимости являются нелинейными, но, если в первом случае строить график S от 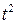 , а во втором ln R от
, а во втором ln R от 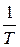 , то оба графика будут представлять из себя прямые линии. Тангенс угла наклона прямой к оси
, то оба графика будут представлять из себя прямые линии. Тангенс угла наклона прямой к оси 
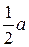 в первом случае и
в первом случае и 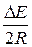 – во втором, вторая прямая пересекает ось ln R в точке ln A.
– во втором, вторая прямая пересекает ось ln R в точке ln A.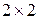 количественным критерием является сумма квадратов отклонений «теоретических»
количественным критерием является сумма квадратов отклонений «теоретических» 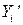 от «экспериментальных»
от «экспериментальных» 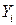 ; точек (квадраты берутся для того, чтобы избежать взаимной компенсации положительных и отрицательных отклонений). Метод, использующий этот критерий, носит название метода наименьших квадратов.
; точек (квадраты берутся для того, чтобы избежать взаимной компенсации положительных и отрицательных отклонений). Метод, использующий этот критерий, носит название метода наименьших квадратов.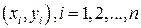
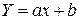 . (22)
. (22)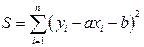 . (23)
. (23)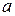 и
и 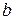 находятся из условия, чтобы
находятся из условия, чтобы 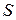 была минимальна. Необходимые условия минимума дают систему уравнений:
была минимальна. Необходимые условия минимума дают систему уравнений: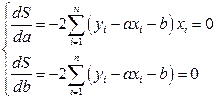 (24)
(24)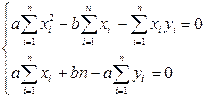 . (25)
. (25)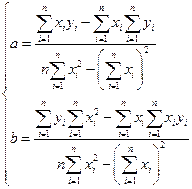 . (26)
. (26)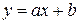 может быть использована как градуировочная для нахождения неизвестного значения
может быть использована как градуировочная для нахождения неизвестного значения  по графику в точке
по графику в точке 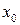 . Погрешность
. Погрешность 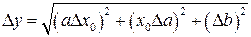 (27)
(27)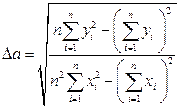 , (28)
, (28)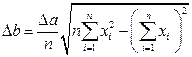 . (29)
. (29)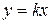 (30)
(30)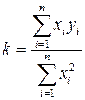 ,
, 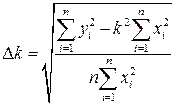 (31)
(31)


