
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка случайных погрешностейСодержание книги
Поиск на нашем сайте Пусть в результате большого числа n измерений получены следующие значения измеряемой физической величины х: х1, х2,... хn. (4) Среднеарифметическое значение величины х равно: Среднеарифметическая погрешность вычисляется по формуле: Среднеквадратическая погрешность определяется по формуле: Грубые оценки интервала, к которому принадлежит истинное значение х измеряемой величины, имеет вид доверительного интервала:
Недостатком оценки (8) является отсутствие данных о степени ее надежности. В связи с этим с помощью теории вероятностей получены более строгие, чем (8) оценки погрешности измерений. Пусть Составим отношение
есть вероятность того, что истинное значение измеряемой величины х принадлежит интервалу. Поскольку Гаусс предложил, что: ошибки разных знаков равновероятны; чем больше ошибка по абсолютной величине, тем меньше ее вероятность; число проделанных измерений n достаточно велико; ширина интервала (9) достаточно мала. При выполнении этих условий, как показал Гаусс, вероятность Р того, что истинное значение измеряемой величины принадлежит интервалу где функция Функция Полученные Гауссом результаты позволили сформулировать и решить вопрос о погрешности измерений при влиянии случайных ошибок. Поставим вопрос следующим образом: указать тот интервал
к которому с заданной вероятностью («надежностью») принадлежит истинное значение измеряемой физической величины х. Этот интервал называют доверительным интервалом. (Обычно в физическом практикуме задается надежность
где величина t, называемая коэффициентом Стьюдента, зависит от числа измерений n, а также от степени требуемой надежности (таблица 1).
Таблица 1 – Значения коэффициентов Стьюдента при различной надежности и разном числе измерений
Относительная ошибка определяется по Формуле Итак, алгоритм обработки результатов многократных измерений физической величины х следующий. 1. Провести n измерений и зафиксировать результаты единичных измерений 2. По формуле (8) определить среднеарифметическое значение 3. Вычислить отклонения единичных измерений от среднеарифметического значения по формуле 4. Вычислить величины 5. Вычислить среднеквадратичную погрешность по формуле (7). 6. Задать надежность р (обычно 7. Вычислить величину 8. Представить результат в стандартном виде с указанием его надежности:
9. Вычислить относительную ошибку по формуле (16).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

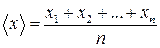 (5)
(5)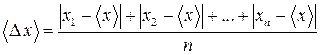 . (6)
. (6)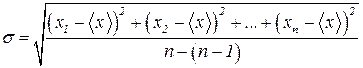 (7)
(7)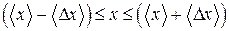 . (8)
. (8)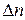 измеренных значений величины x принадлежат интервалу:
измеренных значений величины x принадлежат интервалу: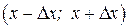 . (9)
. (9)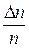 . Величина
. Величина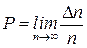 (10)
(10)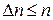 , то вероятность р удовлетворяет условию:
, то вероятность р удовлетворяет условию: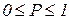 . (11)
. (11)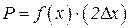 , (12)
, (12)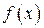 имеет вид:
имеет вид: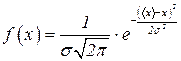 (13)
(13)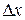 и чем больше число измерений n.
и чем больше число измерений n.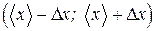 , (14)
, (14)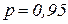
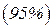 ). Ответ на этот вопрос следующий:
). Ответ на этот вопрос следующий: ,
, 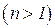 , (15)
, (15)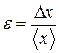 (16)
(16)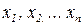 .
.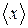 величины х.
величины х.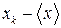
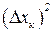 ,
, 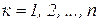 .
.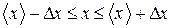 ,
, 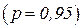 .
.


