
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание экспериментальной установкиСодержание книги
Поиск на нашем сайте
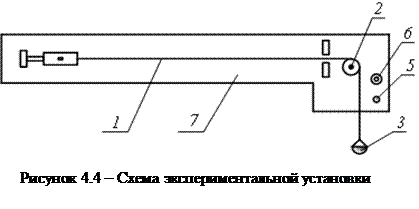
Прибор состоит из струны 1 (смотри рис. 4.4), протянутой через валик 2, на конце которой подвешена чашка для грузов 3. Внешнее периодическое воздействие, необходимое для возбуждения колебаний струны, создается тем, что по струне пропускается переменный ток с частотой 50 Гц, а струна помещается между полюсами электромагнитами. Благодаря этому на струну действует внешняя периодическая сила, частота изменения которой, также, равна 50 Гц. Натяжение нити можно регулировать величиной массы грузика. Прибор включается нажатием кнопки 5, амплитуда колебаний регулируется реостатом 6.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Поместить в чашку 3 груз массой 0,05 кг. Включить вилку прибора в сеть переменного тока. 2. Нажав кнопку 5, плавно увеличить ток в проводе реостатом 6 (начальное положение реостата обеспечивает максимальное сопротивление цепи) пока не будут замечены стоячке волны на фоне экрана 7. 3. Определить устойчивые или неустойчивее колебания. Колебания считается устойчивыми, если узлы стоячих волн легко просматривается, не перемещаясь вдоль экрана 7, и амплитуда их колебаний поперек экрана 7 много меньше амплитуды стоячих волн (пучностей) 4. Наблюдения повторяются после увеличения массы груза на 0,01 кг. 5.Процесс измерений проводится до тех пор, пока масса груза не достигнет 0,6 кГ. Результате измерений заносятся в таблицу 4.1. Таблица 4.1 – Экспериментальные данные
Обозначения "+" и “-” соответствуют устойчивым и неустойчивым колебаниям. ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Частота
где < m > – среднее значение массы груза на интервале устойчивости, соответствующем определенному числу колебаний n. Величина < m >определяется по формуле:
Частота Поскольку основной вклад в погрешность при определении частоты (носится погрешность определения < m >, то абсолютная погрешность вычисляется по формуле:
Абсолютная погрешность т вычисляется по формуле
Истинное значение частоты Результат вычислений занесите в таблицу 4.2 Таблица 4.2– Экспериментальные данные
Длина струны: l =(2,055±0,001) м, диаметр струны: d =(4±0,001)·10–4 м, Плотность меди:
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Продольные и поперечные волки. Является ли колебания струны только поперечными? 2. Длина волны, фронт волны, плоская и сферическая волна. 3. Уравнение плоской, сферической волной. Фаза плоской волны, волновое число, фазовая скорость. Дисперсия волн. 4. Волновое уравнение. 5. Принцип суперпозиции. Групповая скорость. Волновой пакет. 6. Интерференция волн. Условия максимума и минимума. 7. Стоячие волны. Уравнение стоячей волны. Пучности и узлы стоячей волны, их координаты.
ЛИТЕРАТУРA:[1, с.118-121], [3, с.127-205], [4, с.99-115] Лабораторная работа № 1.5
Цель работы: проверить выполнение основного закона вращательного движения с помощью маятника Обербека, сравнив теоретически и экспериментально полученные значения моментов инерции маятника Обербека. Оборудование и материалы: маятник Обербека со шкалой, секундомер, набор грузов, штангенциркуль.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Если дать возможность грузу опускаться, то крестовина начнет вращаться по законам динамики вращательного движения. Обозначим через J момент инерции маятника Обербека, через m – массу груза 5, через r – радиус диска 4. Согласно основному закону динамики вращательного движения:
где М - момент внешних сил относительно оси вращения; ε - угловое ускорение; J - момент инерции относительно оси вращения. Одной из задач данной работы является проверка соотношения (5.1), которую можно осуществлять с помощью экспериментальной установки маятника Обербека. Соотношение (5.1) можно проверить двумя способами: Способ Если момент сил, действующих на крестовину, не меняется (М = const), то в этом случае и J ·ε=const, то есть при изменении момента инерции можно записать:
или
где J 1, J 2 - моменты инерции маятника при различных грузах на стержнях. Пусть момент инерции маятника без грузиков J 1, момент инерции с грузиками J 2, тогда можно записать:
где m 2 R 2 - момент инерции одного груза на стержне крестовины; J 0 - момент инерции без грузиков и стержней крестовины; m1 l 2/3 - момент инерции одного стержня длиной l относительно оси вращения. С учетом (5.3) выражение (5.2) принимает вид:
Угловое ускорение маятника ε связана с линейным ускорением грузила, подвешенного к нити, соотношением:
где r - радиус диска, на который намотана нить; h - путь, пройденный ускоренно движущимся грузом m, подвешенным к нити; t - время, за которое грузик проходит путь h. Тогда
Выражение (5.4) с учетом результата (5.6) принимает вид:
Соотношение (5.7) позволяет проверить справедливость (5.2). Способ Если момент инерции крестовины не меняется (J = const), то в этом случая J ε1 =M1, J ε2 = M2, то есть
Если учесть, что M=FH· r, где FH - сила натяжения нити; r - радиус шкива, (5.8) можно записать в виде:
Из уравнения движения грузила, подвешенного к нити, можно найти натяжение нити
где m - масса груза, подвешенного к нити. С учетом (5.10) и (5.6), для выражения (5.9) имеем:
Убедившись в справедливости равенства (5.11), можем получить еще одно подтверждение справедливости равенства (5.1). Моментом инерции материальной точки относительно какой-либо оси называется произведение массы m на квадрат расстояния r до этой оси: J = m r 2. Моментом инерции тела относительно оси называется сумма моментов инерции всех точек тела относительно оси:
Момент инерции характеризует меру инертности тела к изменению ним угловой скорости ω под действием момента силы М. Из соотношения (5.1) следует, что момент инерции равен:
Если в (5.12) подставить (5.5) и (5.10), получим:
Получается, значение момента инерции крестовины может быть рассчитано по экспериментальными данными измеряемых величин: t, r, h, m 2. Его можно сравнить со значением, полученным из теоретического определения момента инерции:
где J 0 - момент инерции двухступенчатого диска, оси и втулки, то есть маятника без стержней крестовины и грузиков на них; m 1 - масса одного стержня крестовины; l - длина одного стержня крестовины; m 2 - масса одного грузила, закрепленного на стержне маятника; R - расстояние от грузила m2 до оси вращения.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Нажать клавишу "Сеть". При этом освещается цифровое табло индикации времени. 2. Нажать клавишу «Пуск» и намотать нить на диск. Надо внимательно проследить, чтобы на нити не было узлов, а также проверить жесткость крепления грузиков на стержнях крестовины. 3. Платформа с грузиками на свободном конце нити при этом поднимается вверх. Масса грузиков, находящихся на платформе, должна быть неизменна. Установив ее на нужном уровне, который должен остаться неизменным для различных измерений, отжать кнопку «Пуск», при этом крестовина будет неподвижна. 4. Сделать обнуление табло секундомера, нажав клавишу "Сброс". 5. Нажать клавишу «Пуск». Маятник Обербека при этом прейдет в движение. 6. Отсчет времени заканчивается, маятник останавливается вследствие срабатывания нижнего фотодатчика. 7. Для повторных измерений повторить действия, начиная с п. 2. Справочные данные по установке "Маятник Обербека": масса одного постоянного грузила на крестовине - 200 г. масса перегрузок - указанна на перегрузках; масса одного стержня без грузила - 50 г. момент инерции маятника без грузила и стержней крестовины J 0 =2,31 10-5 кг м2. максимальная длина пути движения грузиков - 490 мм. Задание 1. Проверить закон динамики вращательного движения твердого тела первым способом. (М = const) 1. Измерить величины, входящие в формулу (5.7), при М = const. измерения провести 3-5 раз. 2. Результаты опытов занести в таблицу 5.1. Сделать расчеты, выводы, оценить ошибки (см. Приложение А).
Таблица 5.1 – Экспериментальные данные задание 1
Задание 2. С помощью маятника Обербека проверить закон вращательного движения твердого тела вторым способом. (J = const) 1. Измерить величины, входящие в формулу (5.11) при J = const. измерения провести 3-5 раз. 2. Результаты измерений записать в таблицу 5.2.
Таблица 5.2 – Экспериментальные данные задание 2
Задание 3. Определить момент инерции маятника Обербека. 1. Измерить величины, входящие в формулу (5.13). Повторить измерения 3-5 раз. 2. Провести расчеты по формулам (5.13), (5.14). Сделать выводы, оценить ошибки (см. Приложение А).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое момент силы, момент инерции точки, момент инерции тела, угловое ускорение? 2. Напишите основной закон динамики вращательного движения в дифференциальной форме. 3. Сформулируйте основной закон динамики вращательного движения. 4. Укажите способы проверки закона динамики вращательного движения. 5. Напишите связь между линейным ускорением и угловым. 6. Вычисление моментов инерции простейших тел – материальной точки, обруча, диска, стержня, шара.
ЛИТЕРАТУРA:[1, с.72-77], [2, с.53-60], [3, с.127-205], [4, с.99-115] Лабораторная работа № 1.6 Цель работы: проверить выполнение основного закона вращательного движения с помощью маятника Максвелла, сравнив теоретически и экспериментально полученные значения моментов инерции маятника. Оборудование: маятник Максвелла, опорная площадка, измерительная линейка, секундомер, утяжеляющее кольцо. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Принцип действия прибора основан на законе сохранения энергии. В начальном состоянии обе нити намотаны на ось, маятник поднят к опорной площадке и удерживается около нее. После опускания под действием силы тяжести и силы натяжения нитей маятник начинает вращаться и опускаться вниз. При этом потенциальная энергия маятника переходит в кинетическую энергию вращательного движения и кинетическую энергию поступательного движения центра масс маятника. Если центр масс маятника опустился на расстояние h, то по закону сохранения энергии:
где m – масса; J – момент инерции; ω и V – приобретенные угловая скорость и скорость поступательного движения центра масс маятника соответственно, g =9,81м/с2 – ускорение свободного падения. Уравнения движения маятника без учета сил трения о воздух и отклонения нитей от вертикали (оно очень мало) во время плоского движения маятника имеют вид:
где m - масса маятника; J o - момент инерции маятника относительно оси вращения; D0 - наружный диаметр оси маятника; 2F - сила натяжения нитей. Если опускать маятник, начальная скорость его центра масс будет равняться нулю, во время его подъема она отлична от нуля. Для скорости опускания центра масс маятника непосредственно перед его ударом имеем:
где t1 - время движения маятника до удара; h1 - расстояние, на которое опускается маятник за это время. Во время подъема маятника вверх он движется равнозамедленно с ускорением a, направленным как во время его опускания вниз. Скорость движения его центра масс задается уравнением:
где Vс - скорость маятника через время t; Vc2 - начальная скорость движения маятника вверх; t - время, отсчитываемое от начала этого движения. Появление скорости Vc2 обусловлена продолжающимся по инерции вращением маятника в нижней точке его траектории. Намотки при этом вращении нитей на его стержень и приводит к подъему с начальной скоростью Vc2. Величина этой скорости определяется из условия равенства нулю конечной скорости: Vc =0, тогда
где t2 - время подъема маятника до его остановки; h2 - расстояние, пройденное им за это время. Расстояние, пройденное осью маятника во время его подъема, меньше, чем во время его опускании. Разница этих расстояний характеризует уменьшение механической энергии при опускании (или подъема) маятника. С учетом соотношения (6.1), (6.5) или (6.7), получаем для момента инерции:
где t1,2 - время опускания (или подъема) маятника; h1,2 - расстояние, на которое опускается (поднимается) маятник.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.144.139 (0.011 с.) |

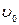 определяется по формуле:
определяется по формуле: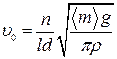 (4.27)
(4.27)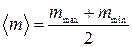 (4.28)
(4.28)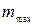 – максимальное значение массы груза на интервале устойчивости,
– максимальное значение массы груза на интервале устойчивости, – минимальное значение массы на интервале устойчивости.
– минимальное значение массы на интервале устойчивости.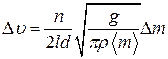 (4.29)
(4.29)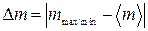 (4.30)
(4.30)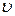 , соответствующее данному значение
, соответствующее данному значение 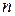 , лежит в интервале;
, лежит в интервале; 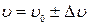
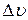
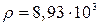 кг/м3
кг/м3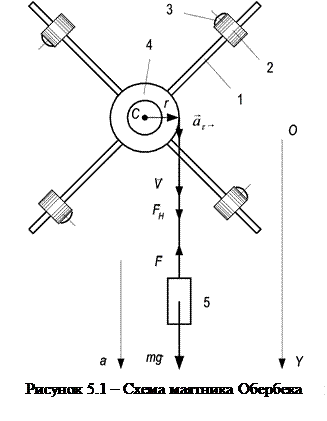 Схема маятника Обербека изображена на рис. 5.1. Он представляет собой крестовину из четырех стержней 1 одинаковой длины и массы, вдоль которых могут перемещаться грузы 2, крепящиеся к стержням винтами 3. Стержни закреплены на втулке, которая может вращаться вокруг горизонтальной оси О. На втулке имеется двухступенчатый диск 4 с намотанной на нем тонкой легкой нерастяжимой нитью, к свободному концу которой привязан груз 5.
Схема маятника Обербека изображена на рис. 5.1. Он представляет собой крестовину из четырех стержней 1 одинаковой длины и массы, вдоль которых могут перемещаться грузы 2, крепящиеся к стержням винтами 3. Стержни закреплены на втулке, которая может вращаться вокруг горизонтальной оси О. На втулке имеется двухступенчатый диск 4 с намотанной на нем тонкой легкой нерастяжимой нитью, к свободному концу которой привязан груз 5.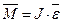 (5.1)
(5.1)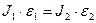 (5.2)
(5.2)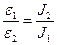
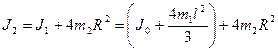 (5.3)
(5.3)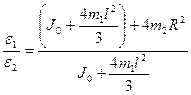 (5.4)
(5.4)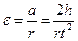 (5.5)
(5.5)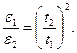 (5.6)
(5.6)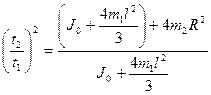 (5.7)
(5.7)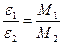 (5.8)
(5.8)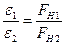 (5.9)
(5.9)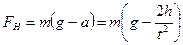 (5.10)
(5.10)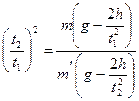 (5.11)
(5.11)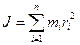
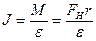 (5.12)
(5.12)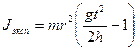 (5.13)
(5.13)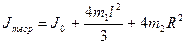 (5.13)
(5.13)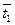
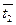
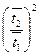
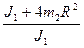
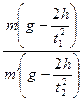
 Упрощенный вид установки для изучения маятника Максвелла и измерения его момента инерции представлен на рис. 6. 1. Маятник состоит из цилиндрической оси 1, диска 2, дополнительного кольца с прорезью 3 и двух нитей одинаковой длины 4. Концы нитей закреплены на опорной площадке 5.
Упрощенный вид установки для изучения маятника Максвелла и измерения его момента инерции представлен на рис. 6. 1. Маятник состоит из цилиндрической оси 1, диска 2, дополнительного кольца с прорезью 3 и двух нитей одинаковой длины 4. Концы нитей закреплены на опорной площадке 5.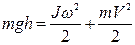 (6.1)
(6.1)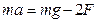 (6.2)
(6.2)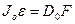 (6.3)
(6.3)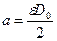 (6.4)
(6.4)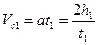 (6.5)
(6.5)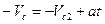 (6.6)
(6.6)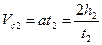 (6.7)
(6.7)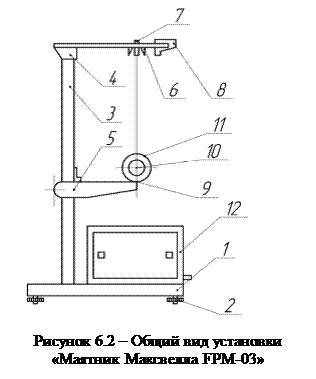
 (6.8)
(6.8)


