
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод дихотомії (поділу навпіл)
В даному випадку загальна кількість обчислень f (x) парна, тобто N = 2 l, l = 1, 2, …, на j -му кроці (j -й ітерації) проводиться пара обчислень Використовують дві умови завершення обчислень: а) виконання заданої кількості обчислень N; б) досягнення заданої величини δ зменшення відрізку локалізації. Алгоритм пошуку мінімуму методом дихотомії полягає в наступному. 1. Задаються N (або δ) та ε, приймається j =1. 2. На j -й ітерації обчислюються
Якщо Якщо 3. Перевіряється умова завершення обчислень: а) Якщо вона виконується, то визначається результуючий відрізок локалізації, оцінки точки мінімуму x * та величини мінімуму f *= f (x *), та обчислення завершуються. Якщо умова не виконується, то приймається j = j +1 та перехід до п.2. Для визначення оцінки точки мінімуму необхідно розглянути всі досліджені точки результуючого відрізку локалізації та обрати одну з них, для якої значення функції буде мінімальним.
Метод Фібоначчі Найкращий з точки зору зменшення відрізку локалізації. На першому кроці проводять два обчислення значень f (x) в точках При обчисленні F 0 = F 1 =1, Fk = Fk −1 + Fk −2, k = 2, 3,.... Умовою завершення обчислень є виконання заданої кількості обчислень N. Алгоритм пошуку мінімуму унімодальної функції методом Фібоначчі полягає в наступному. 1. Задається N, визначаються числа Фібоначчі Fk,
Приймається j =1. 2. На j -й ітерації обчислюються
Якщо Якщо 3. Перевіряється умова завершення обчислень j = N −1. Якщо вона виконується, то визначаються результуючий відрізок локалізації, оцінки точки мінімуму x ∗ та величина мінімуму f * = f (x *) і обчислення припиняються. Якщо умова не виконується, то приймається j = j +1 та перехід до п.2. Примітка. На j -й, j > 1, ітерації обчислюється тільки та точка xi (j), i =1, 2, яка не була визначена на попередній ітерації. Оцінкою точки мінімуму x * є та з точок xi (N-1), i =1, 2, яка залишилась всередині результуючого відрізку локалізації Δ N. Приклад. Визначити методом Фібоначчі мінімум функції f (x) = x 4 − 6 x 2 +10, заданої на відрізку Δ=[1,3], при N =4. Рішення. В даному випадку будуть виконані N −1 = 3 ітерації. Визначаємо числа Фібоначчі Fk, F 0 = F 1 =1, F2 = 2, F3 = 3, F4 = 5, F5 = 8.
Обираємо e=0,1.Результати обчислень записуємо в табл. 2.3. Перша ітерація.
Друга ітерація.
Третя ітерація.
Таблиця 2. 3
Примітка. Знаком * відмічаємо точки xi (j), i =1, 2, що обчислюються на j -й ітерації. Оскільки j = N −1=3, то обчислення завершуються. Точка мінімуму локалізована на відрізку Δ4 = [1,44; 1,88], x *» x 1(3)= 1,028. Метод золотого перетину Недоліком найбільш ефективного методу Фібоначчі є то, що необхідно задавати кількість обчислень N. Метод золотого перетину близький за ефективністю, до методу Фібоначчі, але при цьому не залежить від N. Алгоритм пошуку за методом золотого перетину визначається тем же правилом симетрії, що і алгоритм за методом Фібоначчі: на першій ітерації обираються дві точки, розташовані симетрично відносно середини відрізку; на кожній наступній ітерації обирається одна точка, розташована симетрично до точки, що залишилась. Різниця полягає у виборі точок. Метод золотого перетину заснований на поділі відрізку локалізації «золотим перерізом», тобто коли відношення більшої частини відрізку до всього відрізку дорівнює відношенню меншої частини до більшої.
При такому поділі використовують два дроби Фібоначчі
які задовольняють умовам При оптимізації методом золотого перетину використовуються дві умови завершення обчислень: а) виконання заданої кількості обчислень N, б) досягнення заданої величини δ зменшення відрізку локалізації. Алгоритм пошуку мінімуму унімодальної функції методом золотого перетину полягає в наступному. 1. Задається N (або δ), приймається j =1. 2. На j -й ітерації обчислюються
Якщо Якщо 3. Перевіряється умова завершення обчислень: а) Якщо вона виконується, то визначається результуючий відрізок локалізації точки мінімуму x ∗ та величини мінімуму f * і обчислення завершуються. Якщо умова не виконується, то приймається j = j +1 та перехід до п.2. Порядок виконання роботи 2.1. Відповідно до варіанту за П. 1.1–1.3 знайти мінімум функції одним з чисельних методів оптимізації. Дані взяти з табл. 2.4. 2.2. Побудувати графік функції з табл. 2.4 поблизу точки екстремуму. 3. Звіт має містити результати розрахунків по П. 2.1, графіки функції поблизу точки екстремуму, висновки по роботі. Варіанти Таблиця 2. 4
Контрольні питання 1.Пояснить суть оптимізації методом дихотомії. 2.Розкрити суть оптимізації методом Фібоначчі. 3.Розкрити суть оптимізації методом золотого перетину. 4.Назвати умови застосування розглянутих методів оптимізації. Лабораторна робота № 2.3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 145; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.183.150 (0.021 с.) |
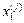 та
та  віддалених на відстань ε / 2 по обидві сторони від середини поточного відрізка локалізації
віддалених на відстань ε / 2 по обидві сторони від середини поточного відрізка локалізації 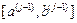 . Якщо
. Якщо 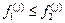 то відкидається частина відрізку, справа від
то відкидається частина відрізку, справа від 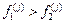 то відкидається частина відрізку, справа від
то відкидається частина відрізку, справа від 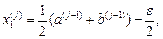
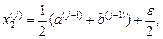
 ,
, 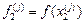 .
.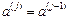 ,
, 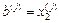 .
.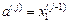 ,
, 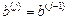 .
.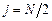 або б)
або б) 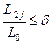 .
.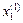 та
та 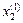 (причому
(причому  ), розташованих симетрично відносно середини відрізку Δ0 = [ a, b ]. За результатами обчислень одна з частин відрізку ([ a,
), розташованих симетрично відносно середини відрізку Δ0 = [ a, b ]. За результатами обчислень одна з частин відрізку ([ a,  , використовуються числа Фібоначчі, які визначаються наступним чином:
, використовуються числа Фібоначчі, які визначаються наступним чином: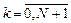 , обирається ε з умови
, обирається ε з умови 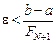 .
.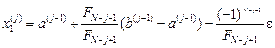 ,
,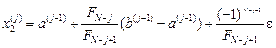 ,
, .
.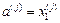 ,
,  .
.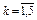 :
:  .
.
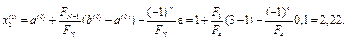

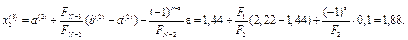

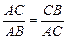 .
.
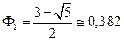 ,
, 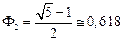 ,
,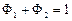 ,
, 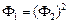 .
. ,
, 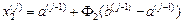 ,
,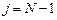 або б)
або б) 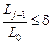 .
.


