
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однофакторный дисперсионный анализ ⇐ ПредыдущаяСтр 7 из 7
Среди различных видов дисперсионного анализа наиболее часто используется однофакторный. Для выполнения однофакторного анализа в опыте должно быть предусмотрено две повторности и более. Исследуемый фактор разбивается на группы с целью выявления оптимальной величины фактора, влияющей на результативный признак. Для облегчения расчета можно уменьшить все показатели в пределах дисперсионного комплекса на определенную величину, а затем увеличить конечные результаты на ту же величину. Географы исследуют не только природные, но и сельскохозяйственные ландшафты (агроландшафты), претерпевающие существенные изменения под воздействием агротехногенеза. Использование системного анализа позволяет не только констатировать изменения в агро-ландшафте, но и активно включаться в его преобразование. Известно, что оптимальным условиям питания растений соответствует дерновая легкосуглинистая гумусированная нейтральная почва. Ее можно создать путем внесения в пахотный горизонт добавок минерального грунта определенного механического состава и торфа. Формирование искусственной антропогенной почвы требует полевых экспериментов. В связи с этим поставлена следующая задача: определить влияние на урожай зерна ячменя разных доз торфа (200, 300, 400 т абсолютно сухого вещества на гектар) при внесении его на фоне минеральных, органических удобрений и доломитовой муки. Исходная почва — дерново-подзолистая глееватая связносупесчаная мелиорированная. После получения сведений об урожайности ячменя в названных условиях составляется таблица дисперсионного комплекса (табл. 3.1), куда заносится исходная информация по группам влияющего фактора (вариантам опыта) и некоторые результаты расчетов (для удобства сделано округление по урожайности до целых чисел). Вначале производим расчет данных по вариантам опыта (строкам). Таблица 3.1 - Однофакторный дисперсионный комплекс
* В числителе — опытные данные, в знаменателе — квадраты этих показателей
Результаты разносим по столбцам. Суммарный урожай ячменя по повторностям После получения данных по вариантам опыта производим расчет необходимых показателей по повторностям (Xk). Сначала суммируем данные урожайности ячменя и приводим в строке под чертой Следующий этап работы — нахождение сумм квадратов отклонений, т. е. расчленение общего варьирования признака на составные части исходя из равенства
где Общая сумма квадратов отклонений вычисляется следующим образом:
Подставив данные из табл. 3.1, получим
где k — число групп фактора, т. е. 4; i — число слагаемых в сумме по вариантам опыта (равно количеству повторностей), т. е. 4. В данном случае должно выдержаться равенство N = ki =4-4=16. По формуле (2.1) вычислим
Сумму квадратов отклонений по повторностям опыта находим по формуле
где i — число повторностей, т. е. 4; k — число слагаемых в каждой сумме Вычисляем
Таблица 3.2 Результаты однофакторного дисперсионного анализа
Сумма квадратов отклонений по остаточному варьированию определяется из равенства
Подставив значение вычисленных сумм соответствующих квадратов отклонений в формулу (3.3), получим
Проводим дисперсионный анализ данных урожая ячменя (табл. 3.2). Вносим в таблицу рассчитанные суммы квадратов отклонений ( Дисперсия определяется путем деления сумм квадратов отклонений ( Оценку сходства или различия между вариантами опыта можно проводить по критерию Фишера, критерию Стьюдента или НСР. Если Fф>Fт (см. табл. 3.2 и приложение 5), то это позволяет сделать вывод, что внесение больших доз торфа положительно влияет на величину урожая ячменя в агроландшафте. Наиболее распространен в дисперсионном анализе для оценки результатов опыта критерий НСР, алгоритм которого приводим ниже. Вначале определяем среднее квадратическое отклонение из дисперсии, полученной в результате случайного варьирования (см. табл. 3.2):
Используя исходные данные, вычислим НСР по указанному выше алгоритму:
НСР0,95 = 0,56-2,26 = 1,26; НСР0;99 = 0,56- 3,25 = 1,82.
Из полученных результатов дисперсионного анализа вытекает следующий вывод (табл. 3.3). Величина НСР0,95 и НСР0,99 меньше величины прибавки урожая зерна ячменя, поэтому внесение высоких доз торфа положительно влияет на урожай. Лучший результат получен в варианте с дозой внесения торфа 400 т/га, где прибавка зерна ячменя составила 15,5 ц/га. Таблица 3.3 Влияние высоких доз торфа на урожай зерна ячменя, ц/га
4. Цели и условия применения информационного метода в географических исследованиях
Научно-техническая революция привела к ускоренному росту объема информации в различных областях науки, включая географию. Математическая теория информации возникла, когда появилась потребность в оценке количества передаваемых сведений. Первоначально она опиралась на отдельные положения теории вероятности; постепенно вырабатывалась собственная методика, определялся свой круг задач. На современном этапе развития теория информации ставит своей целью оценку объема информации, выявление разнообразия в природе, установление различия и сходства в этом разнообразии. По теории вероятности информацию содержат лишь такие данные, которые устраняют существующую до их получения неопределенность. Однако не всегда приходится использовать информацию вероятностного характера, например в картографии, где обычно имеют дело с определенными данными. Это привело к разработке иных подходов в теории информации: комбинаторного и алгоритмического. Комбинаторный подход рассматривает количество информации как функцию числа элементов в конечной совокупности. Он широко используется, например, при измерении объема картографической информации. Алгоритмический подход определяет количество информации как минимальную длину программы, которая позволяет однозначно преобразовать один объект в другой. Существует также представление об информации как о мере разнообразия. В целом разнообразие связано с различием, т. е. с отрицанием неразличимости. Простейшей единицей измерения информации является элементарное различие — различие двух объектов. Чем больше в совокупности попарно различных элементов, тем больше она содержит информации. Если рассматриваемые объекты отождествляются, то информация исчезает. Информационный анализ применяется в некоторых областях географии при соответствующих условиях. В настоящее время разработан способ определения количества информации, содержащейся в рельефе, подсчитан объем информации субаквального биоценоза; ведутся поиски критерия связи на примерах зависимости между физическими свойствами горных пород, климатом и растительностью, компонентами и структурными частями биогеоценозов. Теория информации помогла разработать критерий пространственной дифференциации и однородности. Информационный анализ предпочтительнее использовать для выявления закономерностей в общих, а не частных явлениях.
Весь процесс информационного анализа изучаемого явления можно разбить на следующие этапы. Предварительный этап. При сборе материалов необходимо, чтобы сопоставляемые факторы и явления территориально и во времени соответствовали друг другу во избежание неслучайных ошибок, которые могут привести к возникновению «шума». Факторы и явления должны быть представлены возможно большим числом своих состояний. Они объединяются в более широкие классы в процессе анализа. Анализ информации. После подготовки материала к обработке оценивается связь изучаемого явления с каждым из возможных факторов, из них отбираются наиболее информативные. Рассчитываются попарные каналы связи. Оценивается общая информативность всей совокупности выбранных факторов. Определяется величина «новой информации» и размеры косвенной связи. Процесс моделирования и его оценка. На основе анализа частных каналов связи в сопоставлении с общими строится логическая функция зависимости явлений от совокупности факторов. Оценивается ошибка распознаваний явления по величине «шума» и для составленной логической функции. Проверку достоверности анализа целесообразно проводить и после построения частных каналов связей. Если логическая функция недостаточно полно описывает изменения состояний явления (по распределению ошибок), пытаются найти дополнительные факторы, которые смогли бы улучшить распознающую систему. Прогноз. Если в анализ вошли материалы с достаточным разнообразием состояний и собранные на значительной территории, то прогноз можно осуществить для любой точки, характеристики которой соответствуют состояниям факторов, включенных в анализ. Преимущество информационных методов заключается в том, что они, в отличие от статистического, не требуют применения закона нормального распределения, линейности связей, независимости признаков, метричности и упорядоченности. С практической точки зрения важно уметь численно оценивать степень неопределенности проводимых исследований (энтропия), чтобы их сравнить между собой. Степень неопределенности каждого опыта выражается числом К, поэтому искомая численная характеристика степени неопределенности должна являться функцией числа К. Для К= 1 (неопределенность полностью отсутствует) функция должна обращаться в нуль и возрастать при увеличении числа К. За меру неопределенности опыта (показатель энтропии), имеющего К равновероятных исходов, принято число lg К. Чаще всего пользуются логарифмами при основании два (f (К) =lg2 К). В данном случае за единицу измерения степени неопределенности принимается неопределенность опыта, имеющая два равновероятных исхода (например, при подбрасывании монеты равная вероятность появления орла или решки). Такая единица измерения неопределенности называется двоичной единицей (бит). Если пользоваться десятичными логарифмами, то за единицу степени неопределенности принимается неопределенность опыта, имеющего 10 равновероятных исходов. Такая десятичная единица примерно в 3,32 раза крупнее двоичной единицы (lg210 ≈ 3,32).
Для перевода десятичных единиц в биты полученную величину делят на lg 2 = 0,30103. При применении натуральных логарифмов энтропия выражается в нитах. Если величина энтропии получена с применением натуральных логарифмов, а ее требуется перевести в биты, т. е. в двоичную систему, то этот расчет осуществляется путем деления величины в нитах на ln 2 = 0,69315. Чтобы перевести логарифм числа х с основанием b в логарифм с основанием а, используется формула lgax = lgbx/lgba (5.1)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 66; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.196.182 (0.03 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
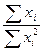
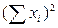

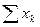
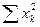 (
(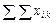 495
495
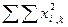 15920
15920
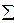 (
(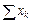 )2
61269
)2
61269
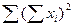 63703
63703
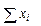 и по каждому варианту опыта вносим в столбец 6 в числителе. Аналогично поступаем с квадратами этих показателей
и по каждому варианту опыта вносим в столбец 6 в числителе. Аналогично поступаем с квадратами этих показателей 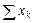 . Суммы сумм урожайности ячменя по вариантам опыта и повторностям должны совпасть и дать сумму всех вариант (
. Суммы сумм урожайности ячменя по вариантам опыта и повторностям должны совпасть и дать сумму всех вариант (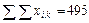 ). Аналогично суммируем квадраты этих показателей по повторностям (
). Аналогично суммируем квадраты этих показателей по повторностям (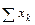 )2 и суммируем их:
)2 и суммируем их:  )2= 61 269. Вычисляем средние арифметические по каждой повторности опыта Mk. Общее среднее арифметическое всех вариант опыта составляет М общ =
)2= 61 269. Вычисляем средние арифметические по каждой повторности опыта Mk. Общее среднее арифметическое всех вариант опыта составляет М общ = 
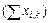 / N = = 495: 16=30,93.
/ N = = 495: 16=30,93.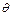 =
= 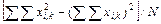
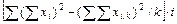 (3.1)
(3.1)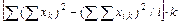 (3.2)
(3.2)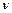
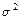
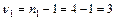 ; по повторностям
; по повторностям 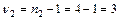 ; по остаточной сумме v3 = v — v1 — v3 = = 15—3—3 = 9.
; по остаточной сумме v3 = v — v1 — v3 = = 15—3—3 = 9.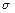 2 =
2 = 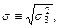 затем вычисляем обобщенную ошибку среднего: тм =
затем вычисляем обобщенную ошибку среднего: тм = 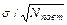 . Поскольку ошибка среднего для всех сравниваемых вариант одна и та же, формула для расчета ошибки разности может быть преобразована: md =
. Поскольку ошибка среднего для всех сравниваемых вариант одна и та же, формула для расчета ошибки разности может быть преобразована: md = 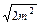 . Наименьшую существенную разность рассчитываем по формуле (1.18).
. Наименьшую существенную разность рассчитываем по формуле (1.18). 0,82; mM = 0,81
0,82; mM = 0,81 
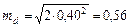 ;
;


