
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Математические методы, используемые для установления подобия и отличия объектов и систем
Вопросы: 1. Критерий Стъюдента (t) 2. Критерий наименьшей существенной разности (НСР) 3. Критерий соответствия (х2) 4. Критерий Фишера (F)
Достоверность различий между генеральными совокупностями (Ni, N 2...) может быть определена с помощью следующих критериев достоверности: критерия Стьюдента (t), наименьшей существенной разности (НСР), критерия соответствия (x2), критерия Фишера (F). 1. Критерий Стьюдента. Сравнение выборочных совокупностей по критерию Стьюдента t позволяет утверждать с некоторой долей уверенности сходство или различие между средними выборок по разнице между ними (Mi — М2, mi — М3, М2 —М3 и т. д.) с использованием формулы t = d/md, (1.14) где d — разность между средними (М1 — М2); т d — ошибка разности средних. При расчете разницы между средними из большей величины вычитают меньшую независимо от нумерации выборочных совокупностей. С методической точки зрения весьма важным для исследователя является установление типа выборочной совокупности. От этого будет зависеть применение соответствующих формул при расчете степени свободы и ошибки разности между средними выборочных совокупностей. Выделяют три типа сравниваемых статистических совокупностей: независимые с одинаковым объемом выборок (Ni = N 2), независимые с разным объемом выборок (N 1 Независимые статистические совокупности могут быть получены на одной или нескольких точках, но при одинаковых условиях проведения эксперимента: например, измерение температуры воздуха в июле в г. Минске в течение нескольких лет и установление достоверных различий между этими показателями по годам исследований; определение содержания бора в автономных ландшафтах на дерново-подзолистых супесчаных почвах одинаковой окультуренности в северной, центральной и южной провинциях Белоруссии и сравнение полученных данных по провинциям. И в том, и в другом случаях условия наблюдения одинаковы. Поэтому при установлении степени свободы в каждом независимом эксперименте выборочные совокупности суммируются. Сопряженные статистические совокупности, как и независимые, однозначны по смыслу, их получают при проведении исследований на одном или нескольких ключах, но в разных условиях. Например: измерение температур воздуха и почвы на глубине 5 см в г. Минске в июле и сравнение полученных показателей (условия разные, точка наблюдения одна и та же); анализ содержания бора в дерново-подзолистых супесчаных почвах элювиального ландшафта и в дерново-подзолистых заболоченных супесчаных почвах супераквального ландшафта (точки наблюдения и условия различны). Степень свободы в каждом рассматриваемом эксперименте определяется по числу пар сравниваемых выборок (Nu).
При одинаковом объеме выборок в случаях независимых статистических совокупностей производят следующие расчеты. Вычисляют средние в сравниваемых выборках М1и М 2. Затем находят ошибки средних для каждой выборки в отдельности по формуле (1.5), определяют разность между средними d =М1 — M 2. Ошибку разности между средними вычисляют по формуле
где т1 — ошибка среднего арифметического первой выборки; т2 — ошибка среднего арифметического второй выборки. Критерий Стьюдента определяют по формуле (1.6). Число степеней свободы устанавливают следующим образом: v =N1 + N2 - 2. Сопоставляя tф, и tТ, устанавливают или отвергают с некоторой долей уверенности различия между средними арифметическими выборок.
Пример. При исследовании глубины расчленения рельефа в Воложинском районе n 1 и Браславском районе N 2 необходимо установить, объединять рассматриваемые участки в один геоморфологический район по степени расчленения рельефа или различать их как самостоятельные. Исходные данные и их обработка приводятся в табл. 1.3. Из полученной информации по средним арифметическим (M1 =16,6, М2 = 15,2 м) различие по глубине расчленения рельефа можно признать как существенным, так и несущественным. Для объективных выводов используем критерий Стьюдента. Определим разницу между средними: d = М1 — М2 = 16,6 — 15,2 = 1,4 м. Ошибки средних по каждой выборке равны:
Ошибка разности средних составляет:
Сопоставляем табличные значения критерия Стьюдента tт=2,32 и 3,36 (см. приложение 4) при Р=0,95 и 0,99 для v=8 с расчетным. Поскольку tТ > t Ф,, то разность между средними признается несущественной (недостоверной). Следовательно, при выделении геоморфологических районов по глубине расчленения рельефа рассматриваемые участки необходимо объединить в один геоморфологический район. Таблица 1.3 Форма обработки вариант в независимых совокупностях
При разном объеме выборок в сравниваемых совокупностях порядок вычислений критерия Стьюдента такой же, как и при установлении достоверности в независимых выборках с одинаковым числом наблюдений. Различие состоит лишь в вычислении ошибки разности средних, которая определяется по формуле
где Σ(xi1 — M1)2 - сумма квадратов отклонений от среднего для первой выборки; Σ (х i 2 - М2)2 - второй выборки; N1, N2— количество вариант в первой и второй выборках соответственно. Исходные данные для формулы (1.16) получаем путем вычислений, аналогичных представленным в табл. 1.3. При малых объемах независимых совокупностей, если дисперсии сравниваемых выборок нельзя считать одинаковыми, число степеней свободы определяется несколько сложнее:
где При установлении различий между сопряженными выборками алгоритм тот же, что и для независимых наблюдений. Вычисление ошибки разности средних в этом случае производится по формулам
где di — разность между индивидуальными сопряженными вариантами в выборках; Число степеней свободы находят по равенству v = Nп—1.
Пример. Сравним глубину расчленения рельефа в пределах конечно-моренного ландшафта N 1 и донно-моренного ландшафта N 2 (получены сопряженные выборки). Для обработки данных составляем табл. 1.4. Число пар NП = 5. Разность между средними
или
Критерий Стьюдента определяется по формуле
Подставив в формулу (1.17) необходимые данные, получим: t =1,4:0,40=3,5. Число степеней свободы v=NП—2 = 5—2=3. Для v=3 при Р=0,95 и 0,99 tT=3,18 и 5,84 соответственно (см. приложение 4). Поскольку t Ф > t Т при Р=0,95, то различие по глубине расчленения рельефа в сравниваемых ландшафтах признается существенным. Такие ландшафты в один геоморфологический район объединять нельзя. Таблица 1.4 Форма обработки данных сопряженных наблюдений
Если при проведении эксперимента пренебречь сопряженностью выборок и обработку статистических показателей проводить по независимым наблюдениям, то получим противоположный вывод, т. е. различие будет признано несущественным. Поэтому необходимо подбирать такой способ обработки выборочных совокупностей, который соответствовал бы условиям проведения опыта.
2. Наименьшая существенная разность. Достоверность различий между двумя выборками может быть проверена по наименьшей существенной разности (НСР). Наименьшая существенная разность показывает то минимальное различие между средними, начиная с которого при выбранном уровне вероятности средние сравниваемые показатели существенно отличаются друг от друга. Величина критерия НСР выражается в тех же единицах, что и сравниваемые средние выборочных совокупностей, и определяется по формуле
НСР = t Т · m d, (1.18)
где т d — ошибка разности средних; tT — табличное значение критерия Стьюдента при выбранном значении уровня вероятности. Если разность между сравниваемыми средними в условиях эксперимента больше или равна величине НСР при Р = 0,95 или 0,99, то различие существенно. Если разность между средними меньше НСР, то различие обусловлено случайными факторами и признается недостоверным. Проверим достоверность разности между средними арифметическими с использованием критерия НСР для случаев независимого и сопряженного наблюдений по формуле (1.18): НСР0,95=2,31•1,20=2,77 м, НСР0,99=3,36-1,20=4,03 м для независимых наблюдений; НСР0,95 = 3,18- 0,40= 1,27 м, НСР0,99 = 5,84 -0,40 = 2,33 м для сопряженных наблюдений. Разница между средними арифметическими глубины расчленения рельефа при независимых и сопряженных наблюдениях в примерах одна и та же (1,4 м). Сравнивая ее с величиной НСР, приходим к тем же выводам, что и при использовании критерия Стьюдента. По величине НСР достоверное различие между средними установлено лишь при сопряженном наблюдении для уровня вероятности 0,95 (HCP0,95=1,27< 3. Критерий Фишера. Сравниваемые совокупности могут отличаться не только по величине средних, но и по другим параметрам распределения случайных величин, в частности по дисперсиям. В таких случаях при установлении достоверности различия между совокупностями лучше использовать критерий Фишера F (положительное асимметричное распределение). Расчет критерия Фишера производится по формуле
где Пример. Необходимо установить достоверность различия в содержании гумуса в дерново-подзолистой заболоченной суглинистой почве для северной n 1 и центральной n 2 провинций РБ. Количество вариант в обеих совокупностях одинаковое. В результате обработки данных получены следующие средние и дисперсии: M1 = 3,53 %, 4. Критерий кси-квадрат. Количественное изучение явлений требует создания гипотез, с помощью которых можно объяснить эти явления. Чтобы проверить гипотезу, нужно получить ряд опытных данных и сопоставить их с теоретически ожидаемыми согласно гипотезе. Совпадение может служить основанием для принятия гипотезы и подтверждения ее правильности. Степень несоответствия фактических наблюдений теоретически ожидаемым результатам может быть различной. Отсюда возникает задача статистической оценки разницы между расчетными и теоретически ожидаемыми данными. Для этой цели используется критерий кси-квадрат (χ2), или критерий соответствия, который рассчитывается по формуле
где φ, φ' — число наблюдений в опыте фактическое и теоретически ожидаемое. Значения кси-квадрат могут быть только положительными и возрастать от нуля до бесконечности. Если расчетные значения кси-квадрат превышают табличные (приложение 6), то гипотеза о независимости признаков отвергается. Если Достоверность расчетных данных можно также оценить по формуле D = ( Различие считается достоверным, если D Пример. Следует определить число сельских жителей с бронхолегочными заболеваниями, обострение болезни у которых связано с природными условиями местожительства. Для обработки выборочных вариант составляем таблицу 1.5. Всего выявлен 71 больной житель из 639 обследованных одного возраста и пола по 9 человек в каждом населенном пункте. Для обработки данных количество обследованных сгруппировано в 9 классов. Поскольку частота в каждом классе φ, φ' должна быть не менее 5, объединяем первые три и последние два класса в столбцах 2 и 3. Получаем новые классы с частотами 11,15 и 13,8 (всего по 6 классов распределения). Затем производим расчеты, которые позволяют получить критерий кси-квадрат (см. табл. 1.5).
Сравниваем Определим также достоверность кси-квадрат по формуле (1.21): D = (5,43—3)/ Таблица 1.5 Сравнение эмпирических и теоретических частот с использованием критерия кси-квадрат
Полученная величина D=0,99<3, следовательно, рассчитанное значение кси-квадрат показывает достоверное влияние природных условий на распространение бронхолегочных заболеваний.
Тема 4 Использование дисперсионного, информационного и кластерного анализа в классифи кации и районировании Вопросы: 1. Обработка данных дисперсионного анализа 2. Цели и условия применения информационного метода в географических исследованиях 3. Цели и условия использования кластерного анализа.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 166; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.193.129 (0.039 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 N 2), сопряженные только с одинаковым объемом выборок (ni = n 2).
N 2), сопряженные только с одинаковым объемом выборок (ni = n 2).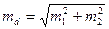 , (1.15)
, (1.15) ;
;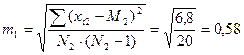 .
. . Полученные данные подставляем в формулу (1.14): t=1,4: 1,2 = 1,17. Число степеней свободы v = N1 + N2 — 2 = 5 + 5 — 2 = 8.
. Полученные данные подставляем в формулу (1.14): t=1,4: 1,2 = 1,17. Число степеней свободы v = N1 + N2 — 2 = 5 + 5 — 2 = 8.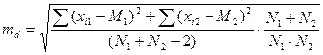 , (1.16)
, (1.16)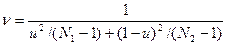 ,
,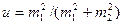 , m1, m2— ошибка среднего первой и второй выборок соответственно.
, m1, m2— ошибка среднего первой и второй выборок соответственно. ;
; 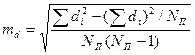 ,
,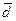 — разность между средними сопряженных выборок; N П — число сопряженных пар в сопря-женных выборках.
— разность между средними сопряженных выборок; N П — число сопряженных пар в сопря-женных выборках.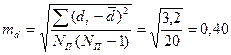
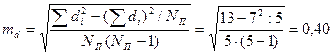 .
.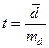 . (1.17)
. (1.17)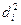
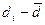
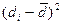
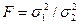 , (1.19)
, (1.19)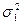 по абсолютной величине должна быть больше, чем
по абсолютной величине должна быть больше, чем 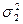 . Если величина расчетного критерия Фишера FФ не превышает величины приведенного в таблице FT (приложение 5), то различие между сравниваемыми дисперсиями считается недостоверным. При Fф>Fт эти дисперсии достоверно различны, а различие сравниваемых генеральных совокупностей признается неодинаковым. Степень свободы рассчитывается для сравниваемых совокупностей отдельно по формуле v = N—1.
. Если величина расчетного критерия Фишера FФ не превышает величины приведенного в таблице FT (приложение 5), то различие между сравниваемыми дисперсиями считается недостоверным. При Fф>Fт эти дисперсии достоверно различны, а различие сравниваемых генеральных совокупностей признается неодинаковым. Степень свободы рассчитывается для сравниваемых совокупностей отдельно по формуле v = N—1.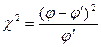 (1.20)
(1.20)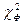 <
< 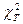 , то признаки можно считать независимыми. Степень свободы при проверке гипотезы о нормальном распределении вычисляется по формуле v = k —3, где k — число классов.
, то признаки можно считать независимыми. Степень свободы при проверке гипотезы о нормальном распределении вычисляется по формуле v = k —3, где k — число классов.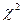 — v)/
— v)/ 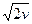
 3. (1.21)
3. (1.21)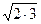 = 0,99.
= 0,99. 10
15
12
10
10
15
12
10
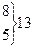
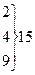 13
14
10
11
13
14
10
11
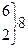
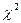 =5,43
=5,43


