Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные выборочные параметры
Характеристику генеральной совокупности дают по параметрам, полученным на основании выборки. Основные выборочные параметры подразделяют на три группы. Первую группу образуют показатели среднего положения, или центральной тенденции. К ним относятся мода, медиана, различные виды средних. Они выражаются именованными величинами, т. е. сохраняют размерность признака. Вторую группу образуют показатели разнообразия признака (разброса, изменчивости): среднее квадратическое отклонение, квадрат отклонений, коэффициент вариации. Третью группу образуют показатели формы распределения: показатели асимметрии и эксцесса. Рассмотрим все три группы показателей. Показатели среднего положения. Для того чтобы получить достаточно обоснованное представление о генеральной совокупности на основании выборки, необходимо использовать наиболее характерные параметры признака. К ним относятся показатели среднего положения: непараметрические, т. е. менее точные (мода, медиана) и параметрические, т. е. более точные (средние величины: арифметическое, гармоническое, квадратическое, кубическое, геометрическое). Мода (Мо) представляет собой наиболее часто встречающуюся варианту в вариационном ряду. На графике она соответствует максимальной ординате и находится на вершине вариационной кривой. Если вариационный ряд разбит на классы, то мода соответствует максимальной частоте класса, который называется модальным, и определяется по формуле:
где хм — меньший предел модального класса: i — классовый интервал; f 1 — частота класса, предшествующего модальному; f 2 — частота модального класса; f 3 — частота класса, следующего за модальным. При полимодальном (многовершинном) распределении вариационный ряд имеет несколько значений моды. Медиана (Me) представляет собой среднюю варианту в ранжированном вариационном ряду, которая делит его на две равные по числу вариант части. При нечетном числе вариант середину ряда будет составлять одна варианта (медиана). При четном числе вариант середину ряда образуют две варианты, среднее арифметическое которых будет характеризовать медиану. При группировке вариационного ряда в классы медиану определяют по следующей формуле:
где хМе — начало класса, в котором находится медиана; N — объем выборки; Σf — сумма частот всех классов, предшествующих модальному классу; fM о — частота модального класса. При наличии в вариационном ряду сильно отличающихся вариант медиана будет характеризовать середину ряда более точно, чем среднее арифметическое. Мода и медиана используются в тех случаях, когда о выборочных параметрах необходимо иметь ориентировочное представление. Среднее арифметическое (М, х ) представляет собой величину, сумма положительных и отрицательных отклонений от которой равна нулю. Оно является основной характеристикой статистической совокупности. Для невзвешенного вариационного ряда среднее арифметическое вычисляется по формуле M = Σ x / N, где Σx — сумма всех вариант совокупности.
Пример. Определено следующее количество осадков, выпав ших в трех пунктах наблюдений: 10, 15 и 20 мм (N =3); M = (10+15+20):3=15 мм.
тм = σ/√ N, (1.1)
где σ — среднее квадратическое отклонение.
t Ф =М/тм. (1.1)
Расчетное значение критерия Стьюдента для оценки достоверности среднего арифметического в примере составит tф = 15: 2,9 = 5,7. Расчетный критерий Стьюдента tФ сопоставляют с его табличным значением tт (приложение 4). Для этого необходимо знать число степеней свободы v и уровень вероятности, или доверительную вероятность Р. Среднее гармоническое (Mгар) используется при усреднении меняющихся скоростей протекания природных процессов и показателей обратно пропорциональной зависимости между природными процессами или явлениями. Среднее гармоническое для невзвешенного вариационного ряда определяется по формуле:
Для расчета среднего гармонического сохраним те же данные, что и для расчета среднего арифметического (см. с. 21).
Пример. При измерении скорости воды в реке на трех отрезках русла получены следующие результаты: 10, 15 и 20 м/с. Среднее гармоническое составит:
Если среднюю скорость воды в реке рассчитывать по среднему арифметическому, то ее величина составит 15 м/с. Различие считается существенным в тех случаях, когда необходима высокая точность. Среднее квадратическое (МКВ) используется, когда необходима проверка результатов эксперимента на единство суммарного действия (например, требуется определить средний радиус или диаметр исследуемого объекта). Для невзвешенного ряда используется формула:
Для расчета среднего квадратического применяем те же данные, что и в предыдущих примерах, но характеризующие другой признак. Пример. Имеются данные по величине радиусов трех спилов Дуба: 10, 15, 20 см. В данном случае вместо среднего арифметического при расчетах следует использовать среднее квадратическое:
Среднее кубическое (Мкуб) применяется в тех же случаях, что и среднее квадратическое, т. е. При проверке на единство суммарного действия (например, при нахождении объема), и определяется по формуле:
Пример. Кубатура древесины по трем ключевым участкам составила 10, 15, 20 м3. Среднее кубическое равно
Эта величина существенно отличается от среднего арифметического. Среднее геометрическое (Мг) необходимо для расчета в случаях, когда требуется определить средние темпы прироста (например, сельскохозяйственной продукции или вегетативной массы деревьев за вегетационный период и т. д.). Этот показатель дает более точное представление о приросте по сравнению со средним арифметическим и рассчитывается по формуле
Пример. Увеличение опада за июнь, июль и август в лист венном лесу составило соответственно 10, 15, 20 г/м2. Определяем среднее геометрическое: При наличии нулевого показателя вместо среднего геометрического вычисляется приближенное среднее арифметическое. По абсолютной величине рассмотренные выше средние значения располагаются в следующем порядке: Мгар<=Мг<=М<=Мкв<=Мкуб. Степень различия между средними зависит от величины коэффициента вариации рассматриваемой совокупности: чем больше коэффициент вариации, тем сильнее различаются по величине показатели среднего положения.
Показатели разнообразия признаков. В каждой совокупности варианты отклоняются от среднего значения. Поэтому для изучаемой статистической выборки недостаточно определить лишь среднее значение, необходимы показатели, характеризующие степень разнообразия совокупности. К показателям разнообразия признаков относятся максимальная и минимальная величины в вариационном ряду (лимит), амплитуда варьирования, среднее квадратическое отклонение, квадрат отклонений от среднего, коэффициент вариации. Эти показатели признаков характеризуют различную степень и особенности разброса. Разность между максимальной и минимальной вариантами (lim) характеризует амплитуду варьирования. Чем ближе минимальные и максимальные варианты к среднему и чем меньше амплитуда варьирования, тем меньше степень разнообразия между переменными в вариационном ряду, тем надежнее характеризуют статистические показатели искомую закономерность. Более точно степень разнообразия признака можно характеризовать другими показателями. Среднее квадратическое отклонение, или сигма (а), показывает степень рассеяния значений статистической совокупности около среднего значения. Среднее квадратическое отклонение определяется для невзвешенного ряда по формуле
для взвешенного — по формуле
где Xi — индивидуальная варианта совокупности; Xi — М — отклонение от среднего индивидуальных вариант; (х — M)2 f — сумма произведений квадратов отклонений вариант от среднего на соответствующие частоты. Для получения исходных данных составляется табл. 1. Подставив в формулу полученные данные, определяем σ =
Таблица 1. Форма записи и расчета среднего квадратического отклонения
Пример. Среднее арифметическое относительной высоты хол мов составляет M =24,54 м, σ =3,17 м. Вариационный ряд высоты холмов следующий: 20,20, 22, 23, 24, 25, 25, 26, 27, 28, 30 м. Исходя из величины σ можно сделать вывод, что до 68,0% вариант в ста тистической совокупности находятся в пределах от 21,33 (24,54 — —3,17=21,33) до 27,71 м (24,54+3,17=27,71). Лишь 32,0% вариант выходит за пределы указанных значений (эти варианты не выделены).
Ошибка среднего квадратического отклонения определяется по формуле mσ =
Точность вычисления ошибок среднего квадратического отклонения и среднего арифметического можно проверить приближенно при помощи соотношения: т σ /тм— = 0,70711. Если соотношение окажется близким к 0,7, то полученные результаты вычислений следует считать репрезентативными. В противном случае необходимо проверить расчет. При получении тех же результатов приходим к выводу, что изучаемое явление не соответствует закону нормального распределения и его оценку следует проводить с использованием непараметрических показателей. Средний квадрат отклонений, или дисперсия (σ2) — показатель, характеризующий степень рассеяния значений переменных около среднего значения. Средний квадрат отклонений можно вычислить путем возведения в квадрат показателя среднего квадратического отклонения или определить по формуле
Средний квадрат отклонений выражается в тех же единицах, что и соответствующие показатели среднего положения. Форма записи исходных данных для расчета σ2 такая же, как и для σ (см. табл. 1). В примере σ2 =10,08 м. Исходя из величины дисперсии, можно определить интервал, в пределах которого находятся варианты выборки: от 14,5 м (24,5—10,0) до 34,5 м (24,5+10,0). Минимальное и максимальное значение вариант соответственно составляет 20 и 30 м. При объединении нескольких аналогичных выборок в общую выборочную совокупность можно рассчитать общий средний квадрат отклонений, если имеются сведения о дисперсии по каждой выборке в отдельности:
где σ2i – дисперсия индивидуальной выборки; k – число частных выборок.
Пример. Вычислим общий средний квадрат отклонений для четырех выборок, отражающих содержание кальция в озерных водах Белоруссии: σ 2 1 = 2, N 1 = 8; σ 2 2 = 2,5, N 2 = 6; σ 3 2 =3,0, N 3 = 7; σ 2 4 = 3,5, N 4 = 8. По формуле(1.9) имеем:
По величине общей средней дисперсии легко определить общее значение среднего квадратического отклонения: σобщ = Коэффициент вариации (V) представляет собой относительный показатель разнообразия признаков. По абсолютным значениям среднего квадратического отклонения и дисперсии трудно определить, насколько сильно варьирует признак при сравнении различных по параметрам совокупностей, особенно если они выражаются в разных единицах измерения, но имеют между собой взаимную связь (например, абсолютная влажность воздуха и количество выпавших осадков). В таких случаях сопряженный анализ варьирования признака производится на основании коэффициента вариации. Он показывает отношение величины среднего квадратического отклонения к величине среднего арифметического и выражается в процентах. Чем более однороден по размаху варьирования исследуемый признак, тем меньше будет коэффициент вариации в данной совокупности; соответственно меньшими будут значения среднего квадратического отклонения и дисперсии.
Для числовых величин с одинаковым знаком коэффициент вариации вычисляется по формуле
V = (σ/M)100 (1.10) Если в статистической совокупности имеются показатели с положительным и отрицательным знаком (например, температуры воздуха), то коэффициент вариации рекомендуется вычислять по формуле V = 100 σ /( где \х1\ — числовое выражение наименьшей отрицательной варианты (без минуса). В данном случае имеется в виду, что при вычислении коэффициента вариации среднее арифметическое и среднее квадратическое отклонения должны быть представлены в виде отрезков на числовой оси. Приведем алгоритм вычисления коэффициента вариации для относительных и абсолютных величин. Пример. Температура воздуха в течение суток в октябре составила (в градусах Цельсия): —4, —3, — 1, +1, +3. Среднее арифметическое равно М = — 0,6, среднее квадратическое отклонение σ =1,95. Если не учитывать наличия интервальной шкалы и определять коэффициент вариации по формуле (1.10), то получим следую щую величину: V = (1,95*100): (—0,6) =—325%. Результат противоречит исходным данным, которые фактически характеризуются небольшим размахом варьирования температур в течение суток. Если среднее арифметическое представить как отрезок от точки — 4 до —0,6, то оно равно: |— 4| + |— 0,6| =3,4. Используя формулу (1.11), получаем коэффициент вариации, соответствующий условиям задачи:
По размаху варьирования признака выделяется 5 групп коэффициента вариации. Если изменение признака находится в пределах величины коэффициента вариации 0—10%, то такое варьирование считается малым, при 10—30 —средним, 30—60 — высоким, 60—100 — очень высоким, при более 100% — аномальным. Показатели асимметрии и эксцесса. Распределение частот в изучаемом объекте не всегда подчиняется закону нормального распределения. Это особенно четко проявляется при выражении вариационного ряда в виде графика. Распределение частот может быть представлено асимметричной, островершинной или туповершинной кривой. Асимметрия кривой распределения обусловлена неравномерным размещением вариант по обе стороны от модального значения признака. Если число вариант больше справа от моды, распределение имеет положительную асимметрию, если слева — отрицательную (рис.1). При получении асимметричной кривой следует проверить асимметричность распределения. Если асимметричность не будет доказана, то рассматриваемое распределение относят к симметричному.
М МО МО М х Рис. 1. Асимметричное распределение: а — отрицательная асимметрия, б — положительная асимметрия
Для проверки асимметричности распределения вычисляют коэффициент асимметрии, его ошибку, затем на основании показателя достоверности устанавливают вид кривой распределения. Коэффициент асимметрии находят по формулам Kas = (М — Мо)/ σ или Ка s = (М — Ме)/ σ.
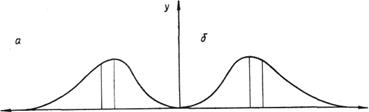
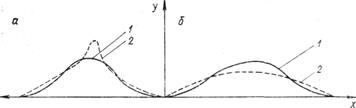
Пример. При изучении содержания подвижного бора в дер ново-подзолистых почвах были получены следующие показатели: M =0,25 мг/кг, Mo =0,28, σ =0,02, N =20. Для получения представ ления о форме кривой распределения бора предварительно вычисляем коэффициент асимметрии: Ка s = (0,25— 0,28): 0,02=— 1,5. Полученная величина указывает на наличие отрицательной асимметрии в распре делении вариант содержания подвижного бора в дерново-подзолис тых почвах. Затем находим ошибку коэффициента асимметрии mas = По условиям задачи она будет равна т as =6: (20+3) =0,29. Достоверность коэффициента асимметрии определяется по кри терию Стьюдента: t = Kas / mas Подставляя необходимые показатели, имеем t =1,5:0,29 = 5,1. Величина критерия Стьюдента (см. приложение 4) для Р=0,99 и при v = oo составляет 2,58 (число степеней свободы принимается равным бесконечности). Рассчитанный критерий достоверности (5,1) больше табличного (2,57), что говорит об асимметричном распреде лении подвижного бора. Если бы расчетная величина критерия Стьюдента была меньше табличной, то распределение отнесли к сим метричному даже при наличии незначительной асимметрии. Эксцесс кривой распределения (Е ) имеет место в тех случаях, когда большинство вариант совокупности сосредоточено около среднего арифметического. Тогда эмпирическая кривая распределения отклоняется от нормальной теоретической кривой у ее вершины и количественно выражается показателем эксцесса (рис. 2). Положительный эксцесс представлен кривой островершинной (эксцессивной, или лептокуртичной) (см. рис. 2, а), отрицательный — плосковершинной (депрессивной, или платикуртичной) (см. рис. 2, b). При сильном отрицательном эксцессе кривая может приобрести вид двухвершинной. Показатель эксцесса определяется по формуле
Е =
Ошибка коэффициента эксцесса вычисляется следующим образом: тЕ = 2 Оценка достоверности показателя эксцесса производится аналогично оценке показателя асимметрии по критерию Стьюдента: t = E / mE. Оценить достоверность показателей эксцесса и асимметрии можно более простым способом. Отклонение эмпирического ряда по асимметрии и эксцессу от нормального распределения считают существенным, если
Рис. 2. Эксцесс кривой распределения положительный (а) и отрицательный (б): 1—теоретическая линия распределения, 2— эмпирическая кривая распределения
Kas и Е более чем в 3 раза превышают свои ошибки (mas, тЕ). Если показатель эксцесса меньше —2, это указывает на наличие в выборке вариант, относящихся к разным совокупностям. Эксцесс считается незначительным, если |E|<0,4. Чем меньше показатель эксцесса, тем ближе распределение к нормальному. Асимметрия и эксцесс эмпирических кривых указывают иногда на важные особенности объекта исследования (например, на изменение признака в ходе дифференциации природно-экологических условий в ландшафте). В таких случаях изучение степени и характера асимметрии и эксцесса вариационных кривых может быть самостоятельной задачей при проведении исследовательских работ. Показатели точности опыта. При исследованиях методического характера обычно приводят точность опыта. Точность опыта показывает, какова величина ошибки среднего арифметического в процентах от величины среднего арифметического, и фактически устанавливает точность определения последней. Показатель точности опыта можно найти по одной из двух формул:
Опыт считается достаточно точным, если р<3%, и удовлетворительным при изменении точности опыта от 3 до 5%. Если значение показателя точности опыта более 5%, к полученным выводам следует относиться осторожно и увеличить число наблюдений или повторностей. Для некоторых исследований методического характера существуют другие градации в оценке точности опыта. Например, при использовании для определения содержания химических элементов в компонентах ландшафта спектрального анализа показатель точности опыта до 15% считается удовлетворительным. Ошибка показателя точности опыта вычисляется следующим образом:
Пример. Среднее арифметическое общей биомассы трав в луговом ландшафте прирусловой поймы M =235 ц/га, ошибка сред него арифметического тм = ±4 ц/га, N=20. Используя формулы (1.12), (1.13), произведем расчет показателей: р = (4: 235)-100 = 1,7%;
Полученная величина точности опыта удовлетворительна.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.196.182 (0.079 с.) |
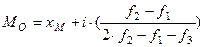 ,
,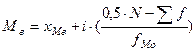 ,
, Среднее арифметическое выборки характеризует среднее арифметическое генеральной совокупности, абсолютная и точная величина которого нам неизвестна. Для точности определения выборочных параметров необходимо установить величину ошибок репрезентативности. Ошибку среднего арифметического выборки обозначают индексом mм. Если тм = 0, величина выборочной совокупности равна величине генеральной совокупности. Ошибка среднего арифметического выборки рассчитывается по формуле:
Среднее арифметическое выборки характеризует среднее арифметическое генеральной совокупности, абсолютная и точная величина которого нам неизвестна. Для точности определения выборочных параметров необходимо установить величину ошибок репрезентативности. Ошибку среднего арифметического выборки обозначают индексом mм. Если тм = 0, величина выборочной совокупности равна величине генеральной совокупности. Ошибка среднего арифметического выборки рассчитывается по формуле: В примере ошибка равна: тм= 5: √ 3 = 2,88 ≈ 2,9. Полученный показатель включается в таблицу экспериментальных данных: М ± mм(15 ± 2,9 мм). Пригодность среднего арифметического выборки для характеристики среднего арифметического генеральной совокупности определяется путем установления достоверности. Досто верность — это априорное убеждение в осуществимости некоторого явления, исключающее всякое сомнение. Достоверность характеризует реализуемость некоторого события, подтверждая его осуществимость высокими значениями уровней вероятности (Р = 0,95; 0,99). Достоверность среднего арифметического оценивают по критерию Стьюдента:
В примере ошибка равна: тм= 5: √ 3 = 2,88 ≈ 2,9. Полученный показатель включается в таблицу экспериментальных данных: М ± mм(15 ± 2,9 мм). Пригодность среднего арифметического выборки для характеристики среднего арифметического генеральной совокупности определяется путем установления достоверности. Досто верность — это априорное убеждение в осуществимости некоторого явления, исключающее всякое сомнение. Достоверность характеризует реализуемость некоторого события, подтверждая его осуществимость высокими значениями уровней вероятности (Р = 0,95; 0,99). Достоверность среднего арифметического оценивают по критерию Стьюдента: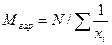
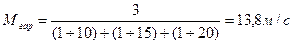
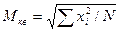 (1.2)
(1.2)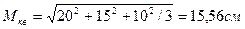
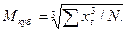 (1.3)
(1.3)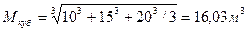
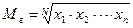 (1.4)
(1.4)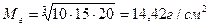
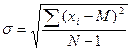 (1.5)
(1.5)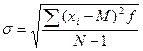 (1.6)
(1.6)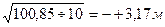 . Если значение σ = 3,17 прибавить к среднему арифметическому и вычесть из него, то определим граничные значения, в которых будет находиться определенная часть вариант исследуемой статистической совокупности.
. Если значение σ = 3,17 прибавить к среднему арифметическому и вычесть из него, то определим граничные значения, в которых будет находиться определенная часть вариант исследуемой статистической совокупности.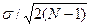 (1.7)
(1.7)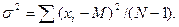 (1.8)
(1.8)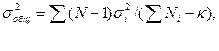 (1.9)
(1.9)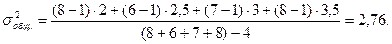
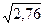 = 1,66.
= 1,66.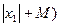 (1.11)
(1.11)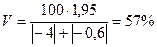
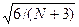 .
.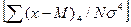 -3.
-3.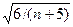
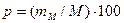 (1.12)
(1.12)