
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 2. Анализ основных статистических параметров, используемых в географииСтр 1 из 7Следующая ⇒
Тема 1. ВВЕДЕНИЕ Вопросы: 1. Понятие математизации географии 2. История развития и современное состояние применения математических методов в географических исследованиях
1. Понятие математизации географии
Развитие географической науки всегда было связано с использованием количественных методов, т. е. применением математики, или математизацией географии. Под математизацией географии (использованием математических методов в географии) понимается обработка экспериментальных данных, математическое моделирование процессов и явлений, применение математического аппарата при установлении закономерностей. Следует различать математизацию географии и математическую географию (В. А. Анучин, 1972). Применение математических методов повышает точность исследований в географии. Нет единого мнения в отношении права на существование математической географии. В. А. Анучин отмечает несостоятельность математической географии как особой отрасли. Б. Л. Гуревич, Ю. Г. Саушкин (1966) под математической географией понимают науку, которая по предмету своему есть география, а по методу — математика. Несколько иное мнение об этом у У. Мересте, X. Яласто (1978): «Математическая география — это отрасль географической науки, которая призвана исследовать возможности и специфику формально-математического подхода к явлениям, изучаемым географией, с целью совершенствования методики исследования в области географии». Однако в настоящее время математическая география как отдельнoe научное направление не существует. В то же время математические методы в географии находят широкое применение. Основные правила при использовании математики в физической географии: - Отсутствие математической обработки данных воспринимается как недостаток эксперимента, так как в современных исследованиях требуется все более четкая и строгая оценка надежности результатов и их квалифицированная математическая обработка. - Применение новых и новейших методов анализа с использованием совершенных методик и вычислительной техники еще не гарантирует высокого качества работы, правильности полученных результатов и требует от географов-исследователей квалифицированного анализа и оценки погрешностей различного происхождения. Поэтому не следует использовать сложные и трудоемкие математические методы в тех случаях, когда задача может быть решена проще и экономичнее.
- При математической обработке данных из-за обилия цифр и формул нельзя терять географическую суть вопроса. В каждой конкретной ситуации надо уметь выбрать наиболее простой и надежный математический прием. Использование метода, не соответствующего данному экспериментальному материалу, может привести к неверным обобщениям и необоснованным выводам. Следует помнить, что каждый из методов математической статистики имеет свои возможности и ограниченную область применения. - Математическая обработка цифрового материала при географических исследованиях необходима для проверки степени надежности и достоверности результатов, для корректного их обобщения, особенно в условиях неопределенности выявляемых закономерностей. - Сложность использования математических методов в физической географии заключается в отсутствии функциональной связи в природе. На объект исследования, кроме основных факторов, влияет множество второстепенных, поэтому рассматриваемые явления и процессы поддаются учету с трудом. Несмотря на трудности, возникающие при разделении сложного природного объекта на части, математические методы позволяют отобрать из многообразия связей ведущие, на основании которых можно строить модели и устанавливать зависимости между природными явлениями, обнаруживать географические закономерности. - Математические методы позволяют также систематизировать и классифицировать результаты исследований и на их основе проводить районирование территории, определять сходство и различие между процессами взаимодействия в различных природных условиях, вероятностную зависимость между явлениями, выделять ведущие факторы, действующие на развитие процесса, создавать математические модели процессов или явлений для целей географического прогнозирования.
2. История развития и современное состояние применения математических методов в географических исследованиях
Впервые математические методы в географии предложено было использовать в 20-е гг. XX в. географами В. П. Семеновым-Тян-Шанским и М. М. Протодьяконовым. Положительно отозвался о возможности применения математики в географии академик А. А. Григорьев в 1934 г. Он считал, что одной из существенных задач физико-географической науки является выработка показателей, характеризующих количественную сторону процесса. Пионером внедрения математики в географию является Д. Л. Арманд (1949). В 1966 г. была опубликована первая работа, посвященная использованию математической статистики в географии (В. А. "Червяков, 1966), позже вышла книга М. К. Бочарова (1971) на эту же тему. Успехи применения математических методов в географии позволили в 1968 г. на базе Московского государственного университета им. М. В. Ломоносова провести первое всесоюзное совещание по данной проблеме. В решении совещания обращалось внимание на необходимость фундаментальной подготовки молодых специалистов в области различных математических дисциплин. Дальнейшее развитие всех областей географической науки дает возможность использовать в экспериментах многие разделы математики (теория информации, теория графов, теория игр, линейная алгебра и др.). В целях обобщения и дальнейшего распространения опыта проводятся очередные всесоюзные совещания (Казань,.1971; Тарту, 1974 и т. д.). На совещании в Тартуском университете впервые была создана секция по математической подготовке географов. Было рекомендовано увеличить количество часов по математике для студентов географических, факультетов, а также ввести спецкурсы и разделы математики, позволяющие шире использовать их в географических исследованиях. С этой целью в БГУ были введены спецкурсы «Теория вероятности» и «ЭВМ и программирование», которые способствуют более квалифицированному внедрению математики в географические исследования. Широко используются математические методы в физической географии учеными Института географии АН СССР, Института географии Сибирского отделения АН СССР, Тихоокеанского института географии ДВНЦ АН СССР, в ряде университетов. Активно внедряются многие разделы математики для решения целого ряда статистических и динамических задач в физической географии учеными зарубежных стран. Опыт этих исследований анализируется в обобщающих работах С. Грегори (1963), Р. Хаггета (1965), Д. Микаеля (1965), П. Т. Матэр (1981). Ряд работ зарубежных авторов посвящены вопросам моделирования (П. Хаггет, Р. Дж. Чорли, 1971; Д. Харвей, 1974), применению интегральных и дифференциальных уравнений в геоморфологии и метеорологии (Г. Самнер, 1981) и др. Математические методы, разработанные для естественных наук, используются в физической географии с соответствующими изменениями.
Правила составления выборок Решение географических задач с использованием математических методов начинается с составления выборки или выборок, которые должны быть репрезентативными и рендомизированными. Репрезентативная выборка должна по возможности наиболее полно и точно характеризовать генеральную совокупность. Это достигается определенными правилами составления. Рендомизация представляет собой научно обоснованный отбор показателей для дальнейшей математической обработки. Репрезентативные совокупности могут быть представлены следующими основными типами отбора: случайным, направленным (типическим), смешанным.
При случайном отборе все объекты имеют одинаковую возможность попасть в выборку.
Пример. Ставится цель изучить гидрологический или гидрохимический режим всех малых рек Беларуси. Для этого из малых рек, названия которых расположены в алфавитном порядке, в выборку включают каждую третью, пятую или десятую, в зависимости от установленного исследователем объема выборки, при соблюдении необходимых условий эксперимента (например, малые реки равнин или малые реки, не испытывающие влияния техногенного воздействия). При этом можно использовать таблицы случайных чисел (приложение 2). Например, необходимо произвести выборку 20 малых рек. Начав с любой колонки приложения 2 и двигаясь по столбцам сверху вниз или снизу вверх, выписывают те первые или последние цифры четырехзначного числа, которые по величине не превосходят 20. Они будут представлять номера тех рек, которые следует включить в выборку. Иногда случайная выборка может не отвечать условиям исследования из-за неоднородности условий. Тогда производят направленный отбор, выбирая для исследования типичные участки. Правила отбора при этом остаются те же, что при случайном отборе. Смешанный отбор производят в тех случаях, когда необходимо дать характеристику неоднородного объекта, например ландшафта. Ландшафт делят на участки, характеризующиеся однородными условиями. В каждом участке производят случайный отбор. Полученные результаты объединяют в одну выборку.
Таблица 1.3 Форма обработки вариант в независимых совокупностях
При разном объеме выборок в сравниваемых совокупностях порядок вычислений критерия Стьюдента такой же, как и при установлении достоверности в независимых выборках с одинаковым числом наблюдений. Различие состоит лишь в вычислении ошибки разности средних, которая определяется по формуле
где Σ(xi1 — M1)2 - сумма квадратов отклонений от среднего для первой выборки; Σ (х i 2 - М2)2 - второй выборки; N1, N2— количество вариант в первой и второй выборках соответственно.
Исходные данные для формулы (1.16) получаем путем вычислений, аналогичных представленным в табл. 1.3. При малых объемах независимых совокупностей, если дисперсии сравниваемых выборок нельзя считать одинаковыми, число степеней свободы определяется несколько сложнее:
где При установлении различий между сопряженными выборками алгоритм тот же, что и для независимых наблюдений. Вычисление ошибки разности средних в этом случае производится по формулам
где di — разность между индивидуальными сопряженными вариантами в выборках; Число степеней свободы находят по равенству v = Nп—1.
Пример. Сравним глубину расчленения рельефа в пределах конечно-моренного ландшафта N 1 и донно-моренного ландшафта N 2 (получены сопряженные выборки). Для обработки данных составляем табл. 1.4. Число пар NП = 5. Разность между средними
или
Критерий Стьюдента определяется по формуле
Подставив в формулу (1.17) необходимые данные, получим: t =1,4:0,40=3,5. Число степеней свободы v=NП—2 = 5—2=3. Для v=3 при Р=0,95 и 0,99 tT=3,18 и 5,84 соответственно (см. приложение 4). Поскольку t Ф > t Т при Р=0,95, то различие по глубине расчленения рельефа в сравниваемых ландшафтах признается существенным. Такие ландшафты в один геоморфологический район объединять нельзя. Таблица 1.4 Форма обработки данных сопряженных наблюдений
Если при проведении эксперимента пренебречь сопряженностью выборок и обработку статистических показателей проводить по независимым наблюдениям, то получим противоположный вывод, т. е. различие будет признано несущественным. Поэтому необходимо подбирать такой способ обработки выборочных совокупностей, который соответствовал бы условиям проведения опыта.
2. Наименьшая существенная разность. Достоверность различий между двумя выборками может быть проверена по наименьшей существенной разности (НСР). Наименьшая существенная разность показывает то минимальное различие между средними, начиная с которого при выбранном уровне вероятности средние сравниваемые показатели существенно отличаются друг от друга. Величина критерия НСР выражается в тех же единицах, что и сравниваемые средние выборочных совокупностей, и определяется по формуле
НСР = t Т · m d, (1.18)
где т d — ошибка разности средних; tT — табличное значение критерия Стьюдента при выбранном значении уровня вероятности. Если разность между сравниваемыми средними в условиях эксперимента больше или равна величине НСР при Р = 0,95 или 0,99, то различие существенно. Если разность между средними меньше НСР, то различие обусловлено случайными факторами и признается недостоверным. Проверим достоверность разности между средними арифметическими с использованием критерия НСР для случаев независимого и сопряженного наблюдений по формуле (1.18): НСР0,95=2,31•1,20=2,77 м, НСР0,99=3,36-1,20=4,03 м для независимых наблюдений; НСР0,95 = 3,18- 0,40= 1,27 м, НСР0,99 = 5,84 -0,40 = 2,33 м для сопряженных наблюдений. Разница между средними арифметическими глубины расчленения рельефа при независимых и сопряженных наблюдениях в примерах одна и та же (1,4 м). Сравнивая ее с величиной НСР, приходим к тем же выводам, что и при использовании критерия Стьюдента. По величине НСР достоверное различие между средними установлено лишь при сопряженном наблюдении для уровня вероятности 0,95 (HCP0,95=1,27< 3. Критерий Фишера. Сравниваемые совокупности могут отличаться не только по величине средних, но и по другим параметрам распределения случайных величин, в частности по дисперсиям. В таких случаях при установлении достоверности различия между совокупностями лучше использовать критерий Фишера F (положительное асимметричное распределение). Расчет критерия Фишера производится по формуле
где Пример. Необходимо установить достоверность различия в содержании гумуса в дерново-подзолистой заболоченной суглинистой почве для северной n 1 и центральной n 2 провинций РБ. Количество вариант в обеих совокупностях одинаковое. В результате обработки данных получены следующие средние и дисперсии: M1 = 3,53 %, 4. Критерий кси-квадрат. Количественное изучение явлений требует создания гипотез, с помощью которых можно объяснить эти явления. Чтобы проверить гипотезу, нужно получить ряд опытных данных и сопоставить их с теоретически ожидаемыми согласно гипотезе. Совпадение может служить основанием для принятия гипотезы и подтверждения ее правильности. Степень несоответствия фактических наблюдений теоретически ожидаемым результатам может быть различной. Отсюда возникает задача статистической оценки разницы между расчетными и теоретически ожидаемыми данными. Для этой цели используется критерий кси-квадрат (χ2), или критерий соответствия, который рассчитывается по формуле
где φ, φ' — число наблюдений в опыте фактическое и теоретически ожидаемое. Значения кси-квадрат могут быть только положительными и возрастать от нуля до бесконечности. Если расчетные значения кси-квадрат превышают табличные (приложение 6), то гипотеза о независимости признаков отвергается. Если Достоверность расчетных данных можно также оценить по формуле D = ( Различие считается достоверным, если D Пример. Следует определить число сельских жителей с бронхолегочными заболеваниями, обострение болезни у которых связано с природными условиями местожительства. Для обработки выборочных вариант составляем таблицу 1.5. Всего выявлен 71 больной житель из 639 обследованных одного возраста и пола по 9 человек в каждом населенном пункте. Для обработки данных количество обследованных сгруппировано в 9 классов. Поскольку частота в каждом классе φ, φ' должна быть не менее 5, объединяем первые три и последние два класса в столбцах 2 и 3. Получаем новые классы с частотами 11,15 и 13,8 (всего по 6 классов распределения). Затем производим расчеты, которые позволяют получить критерий кси-квадрат (см. табл. 1.5). Сравниваем Определим также достоверность кси-квадрат по формуле (1.21): D = (5,43—3)/ Таблица 1.5 Сравнение эмпирических и теоретических частот с использованием критерия кси-квадрат
Полученная величина D=0,99<3, следовательно, рассчитанное значение кси-квадрат показывает достоверное влияние природных условий на распространение бронхолегочных заболеваний.
Тема 4 Использование дисперсионного, информационного и кластерного анализа в классифи кации и районировании Вопросы: 1. Обработка данных дисперсионного анализа 2. Цели и условия применения информационного метода в географических исследованиях 3. Цели и условия использования кластерного анализа.
Таблица 3.1 - Однофакторный дисперсионный комплекс
* В числителе — опытные данные, в знаменателе — квадраты этих показателей
Результаты разносим по столбцам. Суммарный урожай ячменя по повторностям После получения данных по вариантам опыта производим расчет необходимых показателей по повторностям (Xk). Сначала суммируем данные урожайности ячменя и приводим в строке под чертой Следующий этап работы — нахождение сумм квадратов отклонений, т. е. расчленение общего варьирования признака на составные части исходя из равенства
где Общая сумма квадратов отклонений вычисляется следующим образом:
Подставив данные из табл. 3.1, получим
где k — число групп фактора, т. е. 4; i — число слагаемых в сумме по вариантам опыта (равно количеству повторностей), т. е. 4. В данном случае должно выдержаться равенство N = ki =4-4=16. По формуле (2.1) вычислим
Сумму квадратов отклонений по повторностям опыта находим по формуле
где i — число повторностей, т. е. 4; k — число слагаемых в каждой сумме Вычисляем
Таблица 3.2 Результаты однофакторного дисперсионного анализа
Сумма квадратов отклонений по остаточному варьированию определяется из равенства
Подставив значение вычисленных сумм соответствующих квадратов отклонений в формулу (3.3), получим
Проводим дисперсионный анализ данных урожая ячменя (табл. 3.2). Вносим в таблицу рассчитанные суммы квадратов отклонений ( Дисперсия определяется путем деления сумм квадратов отклонений ( Оценку сходства или различия между вариантами опыта можно проводить по критерию Фишера, критерию Стьюдента или НСР. Если Fф>Fт (см. табл. 3.2 и приложение 5), то это позволяет сделать вывод, что внесение больших доз торфа положительно влияет на величину урожая ячменя в агроландшафте. Наиболее распространен в дисперсионном анализе для оценки результатов опыта критерий НСР, алгоритм которого приводим ниже. Вначале определяем среднее квадратическое отклонение из дисперсии, полученной в результате случайного варьирования (см. табл. 3.2):
Используя исходные данные, вычислим НСР по указанному выше алгоритму:
НСР0,95 = 0,56-2,26 = 1,26; НСР0;99 = 0,56- 3,25 = 1,82.
Из полученных результатов дисперсионного анализа вытекает следующий вывод (табл. 3.3). Величина НСР0,95 и НСР0,99 меньше величины прибавки урожая зерна ячменя, поэтому внесение высоких доз торфа положительно влияет на урожай. Лучший результат получен в варианте с дозой внесения торфа 400 т/га, где прибавка зерна ячменя составила 15,5 ц/га. Таблица 3.3 Влияние высоких доз торфа на урожай зерна ячменя, ц/га
4. Цели и условия применения информационного метода в географических исследованиях
Научно-техническая революция привела к ускоренному росту объема информации в различных областях науки, включая географию. Математическая теория информации возникла, когда появилась потребность в оценке количества передаваемых сведений. Первоначально она опиралась на отдельные положения теории вероятности; постепенно вырабатывалась собственная методика, определялся свой круг задач. На современном этапе развития теория информации ставит своей целью оценку объема информации, выявление разнообразия в природе, установление различия и сходства в этом разнообразии. По теории вероятности информацию содержат лишь такие данные, которые устраняют существующую до их получения неопределенность. Однако не всегда приходится использовать информацию вероятностного характера, например в картографии, где обычно имеют дело с определенными данными. Это привело к разработке иных подходов в теории информации: комбинаторного и алгоритмического. Комбинаторный подход рассматривает количество информации как функцию числа элементов в конечной совокупности. Он широко используется, например, при измерении объема картографической информации. Алгоритмический подход определяет количество информации как минимальную длину программы, которая позволяет однозначно преобразовать один объект в другой. Существует также представление об информации как о мере разнообразия. В целом разнообразие связано с различием, т. е. с отрицанием неразличимости. Простейшей единицей измерения информации является элементарное различие — различие двух объектов. Чем больше в совокупности попарно различных элементов, тем больше она содержит информации. Если рассматриваемые объекты отождествляются, то информация исчезает. Информационный анализ применяется в некоторых областях географии при соответствующих условиях. В настоящее время разработан способ определения количества информации, содержащейся в рельефе, подсчитан объем информации субаквального биоценоза; ведутся поиски критерия связи на примерах зависимости между физическими свойствами горных пород, климатом и растительностью, компонентами и структурными частями биогеоценозов. Теория информации помогла разработать критерий пространственной дифференциации и однородности. Информационный анализ предпочтительнее использовать для выявления закономерностей в общих, а не частных явлениях.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-05-11; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.19.251 (0.112 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
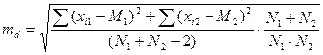 , (1.16)
, (1.16)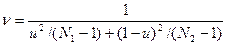 ,
,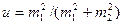 , m1, m2— ошибка среднего первой и второй выборок соответственно.
, m1, m2— ошибка среднего первой и второй выборок соответственно. ;
; 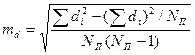 ,
,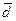 — разность между средними сопряженных выборок; N П — число сопряженных пар в сопря-женных выборках.
— разность между средними сопряженных выборок; N П — число сопряженных пар в сопря-женных выборках.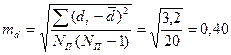
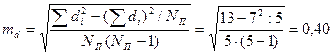 .
.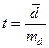 . (1.17)
. (1.17)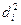
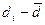
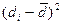
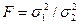 , (1.19)
, (1.19)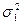 по абсолютной величине должна быть больше, чем
по абсолютной величине должна быть больше, чем 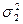 . Если величина расчетного критерия Фишера FФ не превышает величины приведенного в таблице FT (приложение 5), то различие между сравниваемыми дисперсиями считается недостоверным. При Fф>Fт эти дисперсии достоверно различны, а различие сравниваемых генеральных совокупностей признается неодинаковым. Степень свободы рассчитывается для сравниваемых совокупностей отдельно по формуле v = N—1.
. Если величина расчетного критерия Фишера FФ не превышает величины приведенного в таблице FT (приложение 5), то различие между сравниваемыми дисперсиями считается недостоверным. При Fф>Fт эти дисперсии достоверно различны, а различие сравниваемых генеральных совокупностей признается неодинаковым. Степень свободы рассчитывается для сравниваемых совокупностей отдельно по формуле v = N—1.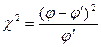 (1.20)
(1.20)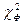 <
< 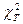 , то признаки можно считать независимыми. Степень свободы при проверке гипотезы о нормальном распределении вычисляется по формуле v = k —3, где k — число классов.
, то признаки можно считать независимыми. Степень свободы при проверке гипотезы о нормальном распределении вычисляется по формуле v = k —3, где k — число классов.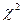 — v)/
— v)/ 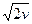
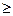 3. (1.21)
3. (1.21)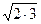 = 0,99.
= 0,99.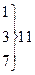 10
15
12
10
10
15
12
10
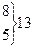
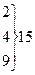 13
14
10
11
13
14
10
11
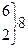
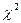 =5,43
=5,43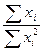
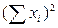

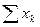
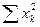 (
(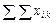 495
495
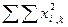 15920
15920
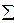 (
(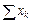 )2
61269
)2
61269
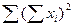 63703
63703
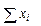 и по каждому варианту опыта вносим в столбец 6 в числителе. Аналогично поступаем с квадратами этих показателей
и по каждому варианту опыта вносим в столбец 6 в числителе. Аналогично поступаем с квадратами этих показателей 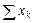 . Суммы сумм урожайности ячменя по вариантам опыта и повторностям должны совпасть и дать сумму всех вариант (
. Суммы сумм урожайности ячменя по вариантам опыта и повторностям должны совпасть и дать сумму всех вариант (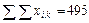 ). Аналогично суммируем квадраты этих показателей по повторностям (
). Аналогично суммируем квадраты этих показателей по повторностям (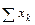 )2 и суммируем их:
)2 и суммируем их:  )2= 61 269. Вычисляем средние арифметические по каждой повторности опыта Mk. Общее среднее арифметическое всех вариант опыта составляет М общ =
)2= 61 269. Вычисляем средние арифметические по каждой повторности опыта Mk. Общее среднее арифметическое всех вариант опыта составляет М общ = 
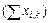 / N = = 495: 16=30,93.
/ N = = 495: 16=30,93.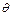 =
= 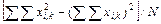
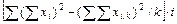 (3.1)
(3.1)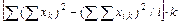 (3.2)
(3.2)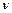
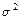
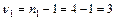 ; по повторностям
; по повторностям 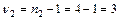 ; по остаточной сумме v3 = v — v1 — v3 = = 15—3—3 = 9.
; по остаточной сумме v3 = v — v1 — v3 = = 15—3—3 = 9.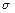 2 =
2 = 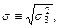 затем вычисляем обобщенную ошибку среднего: тм =
затем вычисляем обобщенную ошибку среднего: тм = 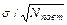 . Поскольку ошибка среднего для всех сравниваемых вариант одна и та же, формула для расчета ошибки разности может быть преобразована: md =
. Поскольку ошибка среднего для всех сравниваемых вариант одна и та же, формула для расчета ошибки разности может быть преобразована: md = 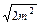 . Наименьшую существенную разность рассчитываем по формуле (1.18).
. Наименьшую существенную разность рассчитываем по формуле (1.18). 0,82; mM = 0,81
0,82; mM = 0,81 
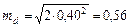 ;
;


