
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В проекциях на оси траекторной системы координатСодержание книги
Поиск на нашем сайте
Движение центра масс самолета описывается первым уравнением системы (1.5), которое после подстановки
Рассмотрим силы, входящие в правую часть векторного уравнения (1.6).
Сила тяги Сила тяжести Отметим, что при отсутствии ветра земная скорость самолета совпадает с его воздушной скоростью ( Если спроектировать векторное уравнение (1.6) на оси траекторной системы координат, то система уравнений движения центра масс самолета при отсутствии ветра и угла скольжения примет вид:
В уравнения (1.7) входит масса самолета, которая в процессе полета может заметно меняться. Поэтому к динамическим уравнениям следует добавить уравнение, описывающее изменение массы самолета:
где Перемещение самолета в пространстве описывается кинематическими уравнениями движения центра масс, которые получаются, если спроектировать векторное кинематическое уравнение
где
где Основной режим движения, рассматриваемый в дальнейшем, это полет без крена (
Как правило, проекция силы тяги на ось С учетом этих допущений уравнения движения самолета в вертикальной плоскости будут иметь вид:
ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА ТРАЕКТОРИЙ САМОЛЕТА В качестве исходных данных для расчета траекторий самолета рассмотрим последовательно его аэродинамические характеристики и характеристики применяемых двигателей.
|
||||||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 , где
, где 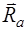 - главный вектор аэродинамических сил и
- главный вектор аэродинамических сил и  - сила тяжести, примет вид
- сила тяжести, примет вид . (1.6)
. (1.6)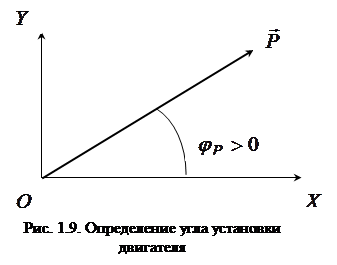 Главный вектор аэродинамических сил
Главный вектор аэродинамических сил 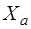 - сила лобового сопротивления (составляющая по оси
- сила лобового сопротивления (составляющая по оси 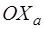 , взятая с обратным знаком);
, взятая с обратным знаком);  - аэродинамическая подъемная сила (составляющая по оси
- аэродинамическая подъемная сила (составляющая по оси 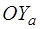 );
); 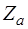 - аэродинамическая боковая сила (составляющая по оси
- аэродинамическая боковая сила (составляющая по оси 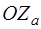 ).
).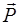 обычно лежит в плоскости симметрии самолета
обычно лежит в плоскости симметрии самолета  и составляет некоторый известный угол
и составляет некоторый известный угол 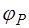 (угол установки двигателя) с положительным направлением оси
(угол установки двигателя) с положительным направлением оси 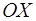 (рис. 1.9).
(рис. 1.9). приложена в центре масс самолета и направлена по местной вертикали вниз.
приложена в центре масс самолета и направлена по местной вертикали вниз. ) и что на большей части траектории полет совершается без скольжения (
) и что на большей части траектории полет совершается без скольжения ( ) или скольжение незначительно.
) или скольжение незначительно. ,
,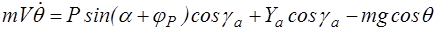 , (1.7)
, (1.7)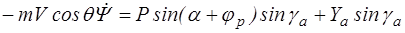 .
.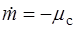 , (1.8)
, (1.8) - секундный массовый расход топлива.
- секундный массовый расход топлива. , (1.9)
, (1.9) - радиус-вектор центра масс самолета, на оси стартовой системы координат
- радиус-вектор центра масс самолета, на оси стартовой системы координат  :
: ,
, , (1.10)
, (1.10)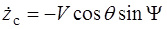 ,
, ,
, 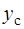 ,
,  - координаты центра масс самолета в стартовой системе координат,
- координаты центра масс самолета в стартовой системе координат,  - высота полета.
- высота полета.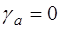 ), т.е. полет в вертикальной плоскости. Тогда от системы (1.7) останутся только первые два уравнения. Во многих случаях полет происходит с малыми углами атаки, угол установки двигателя
), т.е. полет в вертикальной плоскости. Тогда от системы (1.7) останутся только первые два уравнения. Во многих случаях полет происходит с малыми углами атаки, угол установки двигателя  также мал, и поэтому можно считать, что
также мал, и поэтому можно считать, что
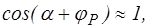
 .
.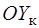 существенно меньше подъемной силы:
существенно меньше подъемной силы:  .
.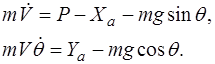 (1.11)
(1.11) Эти уравнения можно получить, спроектировав силы
Эти уравнения можно получить, спроектировав силы 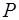 ,
, 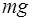 на оси траекторной системы координат, совпадающей при сделанных допущениях со скоростной и связанной (рис. 1.10).
на оси траекторной системы координат, совпадающей при сделанных допущениях со скоростной и связанной (рис. 1.10).


