
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математический аппарат для оценки показателей надежности, применения статистического контроля и статистического регулированияСодержание книги
Поиск на нашем сайте Расчет и оценка показателей надежности, статистический контроль качества продукции и статистическое регулирование технологических процессов базируются на методах теории вероятностей и математической статистики. Основными понятиями теории вероятностей являются случайное событие и случайная величина. В обычном понимании случайное событие – это событие, которое может произойти, а может и не произойти, а случайная величина – это число, связанное со случайным событием. Теория вероятностей, как математическая теория, построена на совокупности аксиом, исходной предпосылкой для определения состава и содержания которых является та реальная ситуация, которая возникает в связи со случайным событием в обычном понимании этого слова. В теории вероятностей под случайным событием понимается элемент некоторого множества элементов, обладающего свойствами, о которых будет сказано ниже. Элементами множеств могут быть любые объекты – результаты работы группы людей, изделия, обладающие теми или иными свойствами, исходы экспериментов или игр – для теории вероятностей как математической дисциплины это безразлично. Подмножество – часть элементов множества, обладающих общим признаком. Суммой или объединением двух множеств называется множество, элементами которого являются элементы обоих множеств. Произведением или пересечением двух множеств называется множество, элементами которого являются лишь те элементы, которые являются одновременно элементами как одного, так и другого множества. Для обозначения суммы множеств применяется знак «+» или «U», для произведения «*» или «∩». Дополнением подмножества А является множество, элементами которого являются элементы, не входящие в А. Для обозначения дополнения применяется черточка над буквой, обозначающей подмножество, или знак отрицания ⌐ перед буквой: ⌐ А. Множество (подмножество) может состоять из одного элемента. Множество, не содержащее элементов, называется пустым. В качестве примера рассмотрим следующую ситуацию. Пример 17. Бригада наладчиков за время работы одной семьи должна наладить и подготовить к сдаче на контроль два агрегата. Возможны два варианта при наладке агрегата – работа может быть выполнена безошибочно или будет допущен дефект, который выявится при контроле. В связи с описанной ситуацией может быть рассмотрено множество
элементами которого являются результаты работы бригады за одну смену:
Если обозначить событие, заключающееся в том, что агрегат не содержит дефектов 1, а событие, заключающееся том, что агрегат содержит хотя бы один дефект 0, то события Этой ситуации можно дать геометрическую интерпретацию, представленную на рис. 3. На этом рисунке событию u1 соответствует точка (1,1), На основе этого множества элементов может быть образована система множеств S, в которую входят различные подмножества множества U, т.е. множество, элементами которого являются различные сочетания элементов из U. Такими подмножествами в рассматриваемом случае являются подмножества (u 1, u 2), (u 1, u 3), (u 1, u 4), (u 2, u 3), (u 2, u 4), (u 3, u 4), (u 1, u 2, u 3), (u 1, u 2, u 4), (u 1, u 3, u 4), (u 2, u 3, u 4). На рис. 3 в качестве иллюстрации выделены подмножества (u 1, u 2) и (u 2, u 3, u 4). Упомянутые ранее свойства множеств определены аксиомами, на которых базируется теория вероятностей. Эти аксиомы были сформулированы русским математиком академиком А.Н. Колмогоровым. Аксиома 1 теории вероятностей заключается в том, что множество S, образованное на основе множества U, обладает следующими свойствами. 1. Система S в качестве элемента содержит все множество U. 2. Если А и В суть подмножества U и входят в S в качестве элементов, то S содержит также A U B, A ∩ B, ⌐ A, ⌐ B. 3. Если совокупность множеств A 1, A 2, …, An, … входит в S, то их сумма и произведение тоже входит в S.
Рис. 3. Геометрическая интерпретация событий
Такое множество называется полем событий. Элементы множества U в теории вероятностей называются элементарными событиями, элементы S – случайными событиями. В рассматриваемом примере элементами множества S являются перечисленные подмножества, а также элементарные события u 1, u 2, u 3, u 4, пустое множество и все множество U = (u 1, u 2, u 3, u 4). Для описания аксиоматики теории вероятностей в качестве объектов изучения используются множества. Аксиоматическая (абстрактная) теория допускает различные конкретные интерпретации, в том числе, конечно, и ту, из которой она возникла. Теория вероятностей возникла как инструмент исследования вопросов, связанных с экспериментами и наблюдениями, которые могут быть повторены много раз в одинаковых условиях, причем результат, выраженный каким-либо образом, может меняться от опыта к опыту. В рассматриваемом примере каждому из входящих в S множеств соответствует их интерпретация на языке событий. Для u 1, u 2, u 3, u 4 интерпретация содержится в их определении. Остальным множествам соответствуют следующие события: (u 1, u 2) – первый агрегат не содержит дефектов; (u 1, u 3) – второй агрегат не содержит дефектов; (u 1, u 4) – результат по дефектности одинаков для обоих агрегатов; (u 2, u 3) – результат по дефектности различен; (u 2, u 4) – второй агрегат дефектен; (u 3, u 4) – первый агрегат дефектен; (u 1, u 2, u 3) – не содержит дефектов хотя бы один агрегат; (u 1, u 2, u 4) – результат по дефектности одинаков или дефектен второй агрегат; (u 1, u 3, u 4) – результат по дефектности одинаков или дефектен первый агрегат; (u 2, u 3, u 4) – содержит дефект хотя бы один агрегат; (u 1, u 2, u 3, u 4) – осуществился любой исход. Эта система удовлетворяет условиям аксиомы 1. Первое из этих условий выполнено по определению множества S: U включено в S. Второе и третье условия также выполнены, что следует из специфики формирования всех элементов множества. Действительно, сумма любых двух подмножеств из S представляет собой подмножество, состоящее из элементов множества U. Но все такие подмножества входят в S. То же можно сказать и о произведении подмножеств и о дополнении к любому подмножеству. Следовательно, рассматриваемое множество S является полем событий. В теории множеств: 1. А и В не пересекаются, то есть не имеют общих элементов, АВ=0. 2. AB…N = 0. 3. AB…N = X. 4. A + B + … + N = X. 5. Дополнительное множество ⌐ A. 6. A = 0. 7. A = U. 8. Система множеств A 1, A 2, …, An образует разложение множества, если A 1 + A 2 + … + An = U. (Это уже предполагает, что множества A 1, A 2, …, An попарно несовместны.) 9. В является подмножеством А. Для случайных событий: 1. События А и В несовместны. 2. События A, B, …, N несовместны. 3. Событие Х заключается в одновременной реализации всех событий A, B,…, N. 4. Событие Х заключается в наступлении по крайне мере одного из событий A, B, …, N. 5. Противоположное событие к А, состоящее в ненаступлении события А. 6. А невозможно. 7. А должно необходимо наступить. 8. Испытание заключается в том, что устанавливают, какое из событий A 1, A 2, …, An происходит; A 1, A 2, …, An называются при этом возможными исходами испытания. 9. Из осуществления события В с необходимостью следует осуществление А. Аксиома 2. Каждому случайному событию A, B, C, … из поля событий поставлено в соответствие неотрицательное число P, называемое его вероятностью. Аксиома 3. P (U) = 1 Аксиома 4. Если события А и В несовместны, то P (A U B) = P (A) + P (B) (теорема сложения). Аксиома 5 является аксиомой математической теории вероятностей, относящейся к случаю бесконечных множеств, соответственно к случаю бесконечного числа случайных событий. Если событие А равносильно наступлению хотя бы одного из попарно несовместных событий A 1, A 2, …, An, …, то P (A) = P (A 1) + P (A 2) + … + P (An) + … (расширенная теорема сложения). Перечисленные особенности множества, называемого полем событий, и соответствующих событиям чисел, называемых вероятностями этих событий, являются теми особенностями, о которых говорилось при определении случайного события. Из сказанного следует, что построенная на основе этого определения теория является абстрактной математической теорией, и ее применение для решения практических задач корректно только в тех случаях, когда объект изучения обладает перечисленными свойствами. В рассматриваемом примере поставим в соответствие каждому событию неотрицательное число, соблюдая при этом условии аксиом 2, 3 и 4. Для этого предположим, что имеются данные о результатах работы бригады за некоторое количество смен n. Пусть за эти смены события u 1, u 2, u 3, u 4 осуществились соответственно n 1, n 2, n 3, n 4 раз. Поставим в соответствие u 1, u 2, u 3, u 4 неотрицательные числа Любому другому событию будет соответствовать число, определяемое как отношение числа осуществлений этого события к общему числу смен работы. Пусть два события А и В несовместны, первое повторилось m 1 раз, второе – m 2 раз. Это значит, что событие А+В повторилось m 1 + m 2 раз, и соответствующее ему положительное число равно
следовательно, справедлива аксиома 4. Рассмотренный пример подтверждает ранее высказанное положение о том, что теория вероятностей возникла как инструмент для исследования повторяющихся в одинаковых условиях экспериментов, технологических процессов, явлений природы, и аксиоматика теории вероятностей создана применительно к этим объектам с учетом их особенностей. Действительно, числа P 1, P 2, P 3 и P 4, удовлетворяющие условию
можно трактовать как частоты осуществления событий u 1, u 2, u 3, u 4 в абстрактной модели многократно повторяющегося явления (в данном случае работы бригады за одну смену), при котором величины P 1, P 2, P 3, P 4 отражают присущее этому явлению свойство. Это свойство трактуется как сохранение устойчивости частот возможных исходов этого явления при его многократном повторении. Смысл выражения «устойчивость частот» может быть раскрыт на примере математической модели, известной под названием «Испытания Бернулли». Рассмотрению этой модели должно предшествовать рассмотрение нескольких новых понятий. Если элементарные события имеют одинаковую вероятность 1/ n, где n – число элементарных событий в исходном множестве U (элементарные события равновероятны), то вероятность случайного события в соответствии с аксиомой 4 равна m / n, где m – число элементарных событий, входящих в это случайное событие. Условной вероятностью события А при условии Н (при гипотезе Н) называется величина
где Н – событие, имеющее положительную вероятность (иначе это выражение не имеет смысла), а А – произвольное событие. Если все элементарные события равновероятны, то условная вероятность P (AH) равна отношению числа элементарных событий, содержащихся в пересечении событий А и Н, к числу элементарных событий, содержащихся в Н. Теоремой умножения вероятностей называется приведенная выше формула, записанная в виде
Эта теорема может быть обобщена на случай трех и более событий. Так, для обобщения ее на случай трех событий А, В, С примем вначале за гипотезу Н = ВС, а затем еще раз применим теорему. В результате получим
Аналогично осуществляется обобщение на случай четырех и более событий. Два события А и Н называются независимыми, если справедливо соотношение
Это понятие позволяет дать формальное определение независимости опытов, которые в реальных условиях принято характеризовать как «опыты, повторяющиеся при неизменных условиях». Рассмотрим пространство элементарных событий U, представляющее некоторый мыслимый опыт. Пусть А1, А2, … - точки пространства U, p 1, p 2, … - соответствующие им вероятности. Возможными исходами двух последовательно проведенных опытов являются пары (Aj, Ak), которые образуют новое пространство элементарных событий. Вероятности в этом пространстве могут быть определены различными способами. Однако при этом должно быть учтено то обстоятельство, что опыты осуществляются в одинаковых условиях, т.е. они независимы, не относятся один к другому как следствие к причине, исход первого не влияет на исход второго. Другими словами, события «исход первого опыта Aj » и «исход второго опыта Ak» должны быть независимы в математическом смысле, то есть
Это равенство определяет вероятность любой пары (Aj, Ak) возможных исходов. Оно может быть использовано как определение вероятностей в новом пространстве элементарных событий, так как величины Предположим, что пространство U состоит из 6 точек – A 1, A 2, A 3, A 4, A 5, A 6, соответствующие им вероятности – p 1, p 2, p 3, p 4, p 5, p 6. Рассмотрим два события – А, содержащее точки A 2, A 3, и В, содержащее точки A 5, A 6. Обозначим символом (А, В) событие «А появилось при первом испытании, В появилось при втором испытании». Тогда
следовательно, события А и В независимы. Таким образом, из соотношения Очевидно также, что они применимы и к последовательности более чем двух испытаний. Под N независимыми испытаниями, соответствующими пространству U,понимается пространство элементарных событий, точками которого являются группы из N исходов, с отнесенными к ним вероятностями, определяемыми как произведение вероятностей этих исходов. Получаемые таким образом пространства называются декартовыми (прямыми) произведениями N множеств. Понятие декартово произведение нуждается в более детальном пояснении. Вначале решим задачу вспомогательного характера. Пример 18. Путнику нужно перейти из пункта А в пункт С, зайдя перед этим в пункт В. Из пункта А в пункт он может пройти четырьмя путями, из пункта В в пункт С – пятью. Сколько всего путей из пункта А в пункт С? Пройдя первый отрезок по пути I, он может второй отрезок пройти пятью пунктами. Следовательно, общее число путей Рассмотренный пример является частным случаем правила декартова произведения конечных множеств. Конечное множество – это множество, состоящее из конечного числа элементов. Декартово произведение множеств – это такое множество, элементами которого являются различные комбинации из представителей перемножаемых множеств. В рассмотренном примере перемножаемыми множествами являются отрезки пути (I, II, III, IV) и (1, 2, 3, 4, 5), их декартовым произведением – различные варианты всего пути:
Правило произведения формулируется так: число элементов в декартовом произведении конечных множеств X и Y равно произведению числа элементов множества X и числа элементов множества Y. В комбинаторике правило произведения обычно формулируется следующим образом: если элемент α можно выбрать k способами, а элемент β – m способами, то пару (α, β) можно выбрать km способами. Комбинаторика – область математики, в которой объектом изучения являются комбинации объектов. Сформулированное правило справедливо и для случая произведения нескольких множеств:
где n () число элементов множества, стоящего в скобках. Возможно, декартово произведение бесконечных множеств. Например, декартова плоскость, т.е. множество пар (x, y), является прямым произведением координатных осей x и y, трехмерное пространство можно рассматривать как произведение трех осей или как произведение плоскости (x, y) на ось z. Вероятности исходов независимых испытаний, определяемых как произведения вероятностей составляющих их исходов каждого испытания, называют прямым произведением вероятностных мер, заданных на множестве U. Повторные независимые испытания, имеющие только два возможных исхода, вероятности которых остаются неизменными для всех испытаний, называются испытаниями Бернулли. Исходы испытаний называют «успехом» У и «неудачей» Н, соответствующие им вероятности обозначаются буквами p и q, их значения неотрицательны и удовлетворяют условию:
Пространство элементарных событий для каждого отдельного испытания состоит из двух точек – У и Н. Пространство элементарных событий для N испытаний Бернулли содержит 2 N точек или последовательностей из N символов У и Н. Каждая точка представляет один возможный исход составного опыта. Так как опыты независимы, вероятность какой-либо последовательности равна произведению, полученному из этой последовательности соответственной заменой букв У и Н на p и q. Так, например,
Если SN – число успехов в N испытаниях, то средняя доля успехов SN / N должна быть близка к p, в этом проявляется «устойчивость частот». Точный смысл этому понятию дает закон больших чисел, который формулируется так: вероятность того, что средняя доля успехов отклоняется от p больше, чем любое наперед заданное число ε, стремится к нулю при возрастании N. Эта одна из форм закона больших чисел, она служит основой интуитивного представления о вероятности как мере действительной частоты. В смысле, соответствующем этому закону, следует понимать выражение «устойчивость частот» при многократном повторении опыта в неизменных условиях. Этот закон доказывается математическими методами, исходная модель также построена математическим методом на основе аксиоматики теории вероятностей. [1] Применительно к потребностям квалиметрии в математической статистике можно выделить две задачи.
1. Оценка неизвестной функции распределения. Задача ставится так: в результате n независимых испытаний объекта, моделью которого является случайная величина ξ, получены следующие значения: x 1, x 2, …, xn. Требуется оценить неизвестную функцию распределения F (x) величины ξ, т.е. определить адекватную теорико-вероятностную модель изучаемого объекта. Другая модификация этой задачи формулируется так: на основании некоторых соображений можно считать, что адекватной моделью наблюдаемых величин является случайная величина с функцией распределения F (x). Необходимо установить, совместимы ли наблюденные значения с гипотезой, что распределение F (x) действительно адекватно реальной ситуации. 2. Оценка неизвестных параметров распределения. Задача ставится так: случайная величина, являющаяся адекватной моделью реальной ситуации, имеет функцию распределения определенного вида, зависящую от k параметров, значения которых неизвестны. На основании наблюдений случайных значений исследуемой величины нужно оценить значение этих параметров. Исходными данными служит совокупность из n наблюдений, в результате которых исследуемая величина принимает значения: x 1, x 2, …, xn. Расположив эти значения в порядке возрастания, можно представить эту последовательность в следующем виде:
Последовательность наблюденных значений исследуемой случайной величины, расположенных в возрастающем порядке, называется вариационным рядом. Функция
называется эмпирической функцией распределения. Это аналог интегрального закона распределения. Аналогом дифференциального закона распределения является гистограмма. Для построения гистограммы интервал возможных значений случайной величины разбивается на некоторое количество интервалов разбиения. Каждый интервал разбиения принимается за основание прямоугольника высоты v/(nh), где h – длина интервала, а v – число выборочных значений случайной величины, попавших в этот интервал. Площадь каждого прямоугольника v/(nh)*h= v/n представляет собой частоту соответствующей группы реализаций случайной величины. На основе анализа эмпирической функции распределения или гистограммы с применением соответствующих критериев делается вывод о виде функции распределения. Абстрактное множество возможных значений случайной величины называется генеральной совокупностью (популяцией), элементы его – реализацией. Группа элементов, наблюденных при исследованиях, экспериментах или на основе производственной или научной практической работы, называется случайной выборкой, полученные значения случайной величины x1, x2, …, xn называются выборочными значениями. Решение первой задачи осуществляется путем нахождения соответствующей меры расхождения между эмпирической функцией распределения и гипотетическим распределением. Эта мера, являясь функцией от случайной величины, т.к. она связана с гипотетическим распределением, также является случайной величиной. Существует ряд критериев, которые устанавливают вид предельного распределения этой случайной величины, - критерий Пирсона, критерий Колмогорова, критерий Смирнова. На основе этого распределения устанавливается область, попадание в которую вычисленной меры расхождения между эмпирическим и гипотетическим распределениями означает согласие между этими распределениями. Эта область охватывает γ % значений меры расхождения, где γ – достаточно близкое к 100 число, чтобы гарантировать уверенность в правильности принятого решения. Оценка неизвестных параметров распределения может быть точечной и интервальной. Среднее арифметическое выборочных значений
называется выборочным средним. Выборочное среднее является случайной величиной (как и любая другая функция выборочных значений), его математическое ожидание равно математическому ожиданию самой случайной величины ξ:
Дисперсия
Соответственно среднеквадратичное отклонение равно Величина
называется выборочной дисперсией, а
выборочным среднеквадратичным отклонением. На основе этих формул вычисляются оценки неизвестных параметров распределений и доверительные интервалы для них. Доверительный интервал – это такой интервал, из которого выбирается значение параметра для создания вероятностной модели изучаемого объекта. Доверительный интервал может быть двусторонний и односторонний. Односторонний доверительный интервал сразу дает оценку неизвестного параметра сверху или снизу. При определении величины выборочной средней и выборочной дисперсии необходимо учитывать характер этих оценок. Оценка называется состоятельной, если при увеличении объема выборки она сходится по вероятности к оцениваемой величине, т.е. вероятность больших отклонений стремится к нулю. Приведенные выше оценки для математического ожидания и дисперсии являются состоятельными. Оценка является несмещенной, если ее математическое ожидание совпадает с соответствующим значением параметра распределения случайной величины. Как было показано, оценка среднего значения является несмещенной. Имеет место соотношение
Поэтому несмещенной оценкой дисперсии будет действительно:
Таким образом, процесс обработки статистических данных, полученных на основе эксперимента или на основе эксплуатационных сведений, включает следующие этапы. 1. Построение вариационного ряда. 2. Построение эмпирической функции распределения и гистограммы. 3. Принятие решения о виде закона распределения случайной величины. 4. Расчет величин оценок для математического ожидания и среднеквадратичного отклонения. Для многих явлений или объектов адекватной математической моделью является смесь. Смесь – случайная величина, закон распределения которой представляется в виде
где fi (x) – закон распределения i -го элемента смеси; α i – доля i -го элемента в смеси; n –число элементов смеси,
Для смеси из двух компонент
|
||
|
Последнее изменение этой страницы: 2021-05-27; просмотров: 160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

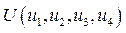 , (95)
, (95)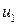 – оба агрегата не содержат дефектов;
– оба агрегата не содержат дефектов;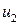 – первый агрегат не содержит дефектов, второй дефектный;
– первый агрегат не содержит дефектов, второй дефектный;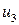 – первый агрегат содержит дефекты, второй без дефектов;
– первый агрегат содержит дефекты, второй без дефектов;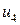 – оба агрегата дефектные.
– оба агрегата дефектные.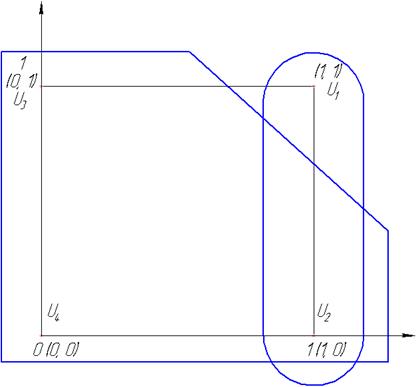
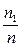 ,
, 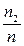 ,
, 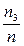 и
и 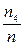 , что согласуется с аксиомой 2. Тогда событию (u 1, u 2, u 3, u 4) соответствует
, что согласуется с аксиомой 2. Тогда событию (u 1, u 2, u 3, u 4) соответствует 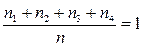 , что согласуется с аксиомой 3.
, что согласуется с аксиомой 3.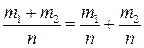 , (96)
, (96)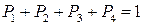 , (97)
, (97)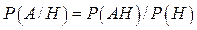 , (98)
, (98)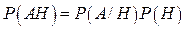 . (99)
. (99)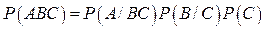 . (100)
. (100)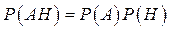 . (101)
. (101)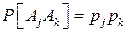 . (102)
. (102)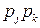 в сумме дают единицу,
в сумме дают единицу, 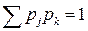 .
.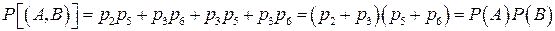 , (103)
, (103)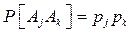 следует, что любое событие, связанное со вторым испытанием, является независимым от любого события, связанного с первым испытанием. Такова математическая интерпретация понятия «независимые опыты», «опыты, осуществляемые в неизменных условиях». Аналогичные рассуждения могут быть проведены для случая, когда пространство U состоит из любого количества точек.
следует, что любое событие, связанное со вторым испытанием, является независимым от любого события, связанного с первым испытанием. Такова математическая интерпретация понятия «независимые опыты», «опыты, осуществляемые в неизменных условиях». Аналогичные рассуждения могут быть проведены для случая, когда пространство U состоит из любого количества точек.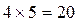 . Если путнику необходимо пройти не два, а три отрезка, то, соответственно, требуемое произведение получится при перемножении трех множителей.
. Если путнику необходимо пройти не два, а три отрезка, то, соответственно, требуемое произведение получится при перемножении трех множителей.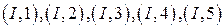 ; (104)
; (104)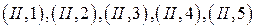 ; (105)
; (105)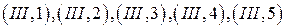 ; (106)
; (106)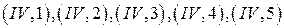 ; (107)
; (107)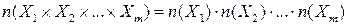 , (108)
, (108)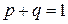 . (109)
. (109)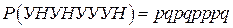 . (110)
. (110)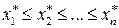 . (111)
. (111)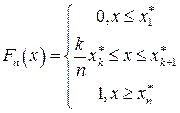 ,
, 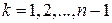 (112)
(112)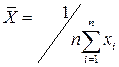 (113)
(113)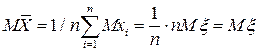 . (114)
. (114)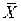 связана с дисперсией ξ соотношением
связана с дисперсией ξ соотношением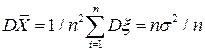 , (115)
, (115)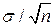 , где
, где 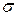 – среднеквадратичное отклонение случайной величины ξ.
– среднеквадратичное отклонение случайной величины ξ.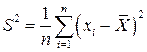 , (116)
, (116)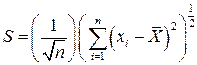 , (117)
, (117)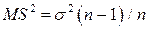 . (118)
. (118)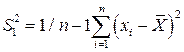 , (119)
, (119)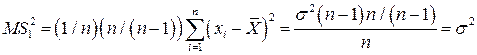 . (120)
. (120)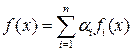 , (121)
, (121)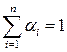 (122)
(122)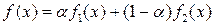 . (123)
. (123)


