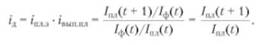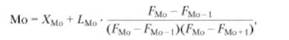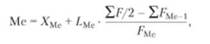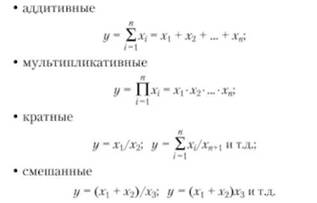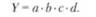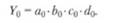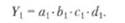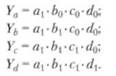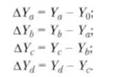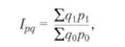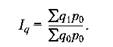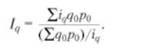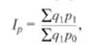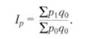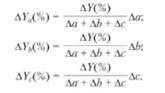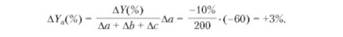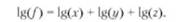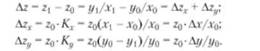Лекция 2. Методы, применяемые на этапе диагностики проблем

Методы, используемые на этапе диагностики проблем, обеспечивают ее достоверное и наиболее полное описание. В их составе выделяют методы сравнения, факторного анализа, моделирования и прогнозирования. Все эти методы осуществляют сбор, хранение, обработку и анализ информации, фиксацию важнейших событий. Набор методов зависит от характера и содержания проблемы, сроков и средств, которые выделяются на этапе постановки.

1. Методы сравнений и 2. факторный анализ являются широко известными и достаточно подробно излагаются в дисциплинах «Анализ хозяйственной деятельности», «Общая теория статистики» и др. Они основываются на сопоставлении фактических и нормативных (плановых, целевых) показателей и выявлении отклонений и основных причин этих отклонений.

 

1. Методы сравнений. Методы относительных и средних величин

Традиционные способы обработки информации и принятия решений связаны, например, со сравнением различных величин между собой во времени и пространстве.

 

· Относительные величины интенсивности - показатели, характеризующие степень распространения или уровень развития того или иного явления в определенной среде.

· Относительные величины координации - показатели, характеризующие соотношение отдельных частей целого между собой. При этом за базу может быть принята любая из частей.

· Относительные величины сравнения - показатели, представляющие собой частное от деления одномерных абсолютных величин, характеризующих разные объекты и относящихся к одному и тому же периоду времени.

· Определение среднего уровня величин (среднегармонических, среднеарифметических, среднегеометрических и других степенных значений, моды, медианы и т.д.).

· Средняя величина - обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. Выбор вида средней определяется экономическим содержанием рассматриваемого показателя и характером исходных данных. Различают следующие виды средних величин: гармоническая, арифметическая, геометрическая, квадратическая, кубическая и т.д.

Перечисленные выше средние относятся к классу степенных средних и выводятся из общей формулы, в которой различны лишь значения показателя степени т

Кроме степенных средних (как простых, так и взвешенных) в экономическом анализе используются структурные средние: мода и медиана.

· Мода - как средняя величина представляет собой наиболее часто встречающееся значение случайной величины, и широко используется при принятии решений на основе изучения покупательского спроса, регистрации цен и т.д.

В интервальных рядах распределения с равными интервалами мода вычисляется по формуле

 

где Х_Мо - нижняя граница модального интервала;

і_Мо - длина модального интервала;

F _Мо, F _{Мо -1}, F _{Мо +1}, - частоты значений в модальном интервале, интервале предшествующем модальному и следующему за модальным.

· Медиана - это вариант, который находится в середине вариационного ряда, т.е. медиана делит ряд на две равные (по числу единиц) части. Медиана находит практическое применение в анализе рынка вследствие особого свойства - сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая.

Значение медианы может быть вычислено методом линейной интерполяции по формуле:

где Х_Ме - нижняя граница медианного интервала;

i _Ме - длина медианного интервала;

∑F/2 - половина от общего числа наблюдений;

∑ F _{Ме -1} - сумма наблюдений, накопленная до начала медианного интервала;

F _Ме - число наблюдений в медианном интервале.

 

2. Факторный анализ. Под факторным (экономическим) анализом понимается постепенный переход от исходной факторной системы (результирующий показатель) к конечной факторной системе, раскрытие полного набора прямых, количественно измеримых факторов, оказывающих влияние на применение результативного показателя. Постановка задачи факторного анализа: пусть y=f(xi) – некоторая функция, характеризующая изменение некоторого результативного показателя или процесса; x1, x2, … xn – факторы, от которых зависит функция y=f(xi). Задана функциональная детерминированная форма связи изучаемого показателя y с набором факторв x1, x2, … xn: y=f(x1, x2, … xn). Пусть показатель y получил приращение (Δy) за анализируемый период. Требуется определить, какой частью численное приращение функции y=f(x1, x2, … xn) обязано приращению каждого аргумента (фактора). Сформулированная таким образом задача есть постановка задачи прямого детермированного факторного анализа.

Примерами прямого детерминированного факторного анализа являются: анализ влияния производительности труда и численности работающих на объем произведенной продукции (y - объем продукции; x, z – факторы; задана функциональная форма связи y=x*z); анализ влияния величины прибыли, стоимости основных производственных фондов и нормируемых оборотных средств на уровень рентабельности (y – уровень рентабельности; x, z, v – соответствующие факторы; заданная функциональная форма связи y=x/(z+v).

При принятии решений на основе детерминированного факторного анализа устанавливается точная функциональная связь между воздействующими факторами х, и результативным показателем у. Наиболее часто в экономическом анализе встречается детерминированное моделирование следующих типов факторных систем:

 

 

В детерминированном факторном анализе одним из ключевых вопросов остается определение величины влияния отдельных факторов на прирост результативных показателей. Для этого используются способы: цепных подстановок; индексный; абсолютных разниц; относительных разниц; пропорционального деления; интегральный; логарифмирования и др.

Первые четыре из перечисленных способов (цепных подстановок, индексный, абсолютных разниц, относительных разниц, пропорционального деления) формируются на принципе элиминирования - исключения воздействия всех факторов на величину результативного показателя, кроме одного. При этом считается, что все факторы независимы, поэтому изменяется вначале один, потом два, затем три и т.д.

· Метод цепных подстановок - заключается в определении ряда промежуточных значений результативного показателя Y путем последовательной замены базисной величины каждого воздействующего факторного на отчетную. В результате обеспечивается выделение влияния каждого фактора. Например, связь между результативным показателем Y и воздействующими факторами a, b, c, d определяется мультипликативной моделью:

Тогда базисное значение Y ₀ рассчитывается по формуле:

Отчетное значение результативного показателя Y ₁ определяется выражением:

Условные значения результативного показателя Y _а, Y_b, Y_c, Y_d рассчитываются соответственно из выражений:

Тогда влияние каждого фактора на результат можно описать в виде:

· Индексный метод – построен на вычислении относительных показателей динамики, пространственных сравнений, выполнения плана (норматива, прогноза) и т.д. Основная форма индекса - агрегатный (складываемый, суммируемый), в котором числитель и знаменатель представляют собой набор ("агрегат") непосредственно несоизмеримых и неподдающихся суммированию элементов - сумму произведений двух величин, одна из которых меняется (индексируется), а другая остается неизменной (вес индекса). Примером общего индекса количественных показателей может служить агрегатный индекс стоимости продукции или товарооборота:

где ∑q₁ p ₁, ∑ q ₀ р₀ - стоимость продукции соответственно отчетного и базисного периодов;

p ₁, р₀ - цены единицы продукции в отчетном и базисном периодах соответственно;

q 1, q ₀ - количество какой-либо продукции в натуральном выражении в отчетном и базисном периодах соответственно.

Индекс I_pq показывает во сколько раз изменилась стоимость продукции отчетного периода по сравнению с базисным.

Агрегатный индекс физического объема продукции I_q отражает изменение только одного фактора - индексируемого показателя объема продукции д, реализуемой по одним и тем же ценам, например базисным р₀:

В аналитических целях может быть также использован общий индекс физического объема I_qпредставленный в форме среднего гармонического индекса

Рассмотренные выше общие индексы рассчитываются для количественных показателей. Наряду с ними широкое распространение получили общие индексы качественных показателей. Характерными примерами общих индексов качественных показателей служат агрегатные индексы цен.

Агрегатный индекс с весами объема продукции по отчетному периоду, предложенный в 1874 г. немецким экономистом Г. Пааше, вычисляют по формуле:

где ∑q₁p₁ - фактическая стоимость товаров в отчетном периоде;

∑ q₁p₀ - условная стоимость товаров, реализованных в отчетном периоде по ценам базисного периода.

Агрегатный индекс с весами объема продукции по базисному периоду, предложенный в 1864 г. немецким экономистом Э. Ласпейресом, вычисляют по формуле:

Значения индексов цен Г. Пааше и Э. Ласпейреса для одних и тех же данных не совпадают, так как имеют различное экономическое содержание. Индекс цен Г. Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде и фактическую экономию (или перерасход) от изменения цен. Индекс цен Э. Ласпейреса характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в базисном периоде и экономию (или перерасход), которую можно было бы получить от изменения цен (т.е. условную экономию).

· Метод абсолютных разниц - Используется в мультипликативных и мультипликативно-аддитивных моделях и заключается в расчете величины влияния факторов умножением абсолютного прироста исследуемого фактора на базовую величину фактора, находящегося справа от него и на фактическую величину факторов, расположенных слева.

· Метод относительных разниц – также используется лишь в мультипликативных и мультипликативно-аддитивных моделях для измерения влияния факторов на прирост результативного показателя. Он заключается в расчете относительных отклонений величин факторных показателей с последующим расчетом изменения результативного показателя за счет каждого фактора относительно базового. Метод относительных разниц, обладая высоким уровнем наглядности, обеспечивает получение тех же результатов, что и метод абсолютных разниц при меньшем объеме вычислений, что достаточно удобно при большом количестве факторов в моделях.

· Метод пропорционального деления (долевого участия) – этот метод заключается в пропорциональном распределении прироста результативного показателя Yза счет изменения каждого из факторов между ними. Например, для аддитивной модели типа Y = а+ b + с влияние рассчитывается как:

Будем считать, что Y - себестоимость продукции; а, b,с - затраты на материалы, оплату труда и амортизацию соответственно. Пусть уровень общей рентабельности предприятия снизился на 10% в связи с увеличением себестоимости продукции на 200 тыс. руб. При этом затраты на материалы сократились на 60 тыс. руб., затраты на оплату труда выросли на 250 тыс. руб., а затраты на амортизацию - на 10 тыс. руб. Тогда за счет первого фактора (а) уровень рентабельности вырос:

За счет второго (b) и третьего (с) факторов уровень рентабельности снизился:

Метод дифференциального исчисления – предполагает, что общее приращение функции различается на слагаемые, где значение каждого из них определяется как произведение соответствующей частной производной на приращение переменной, по которой вычислена данная производная.

Метод простого прибавления неразложимого остатка – подразумевает равномерное распределение этого остатка между факторами.

Метод взвешенных конечных разностей – в данном методе величина влияния каждого фактора определяется по каждому из вариантов подстановки факторов. Затем результаты суммируются и от полученной суммы берется средняя величина, дающая единый ответ о значении влияния фактора.

Логарифмический метод – заключается в логарифмически пропорциональном распределении остатка по искомым факторам и применяется в мультипликативных моделях. Результаты расчетов не зависят от местоположения факторов в модели.

Например, для функции вида f = х + у + z

К достоинству логарифмического метода относятся высокая точность (более высокая, чем при интегральном способе), а также распределение совместного действия факторов пропорционально доле изолированного влияния каждого фактора на уровень результативного показателя. Недостаток логарифмического метода заключается в ограниченной сфере его применения.

· Метод коэффициентов – основан на сопоставлении числовых значений одних и тех же базисных экономических показателей при разных условиях:

Достоинство метода заключается в его относительной простоте. Недостаток - результат суммарного влияния факторов не совпадает с величиной изменения результативного показателя, подсчитанной прямым способом.

· Интегральный метод – недостатком элиминирования как способа детерминированного факторного анализа является предпосылка о том, что факторы изменяются независимо друг от друга. В реальных же задачах факторы изменяются совместно, взаимосвязано, что дает дополнительный прирост результирующего показателя.

 

3. Моделирование включает следующие модели: экономико-математические, теории массового обслуживания, теории запасов и экономического анализа.

а) Экономико-математическое моделирование основывается на использовании однофакторных и многофакторных моделей. Применяются однофакторные модели следующих видов: линейные модели, парабола и гипербола; многофакторные модели: линейная и логарифмическая. Наиболее часто применяются линейные модели – однофакторные

 

y = a₀ + a₁x                   (4.2.1)

 

 

и многофакторные

 

y = a₀ + a₁x₁ … + a_nx_n                       (4.2.2)

 

где a₀, a₁, …, a_n – параметры уравнений, x, x₁ …, x_n – независимые переменные при принятии решений, y – зависимая переменная, описывающая последствия принимаемых решений. Задача состоит в определении параметров уравнения a₀, a₁, …, a_n.

б) Теория массового обслуживания (теория очередей ) применяется для решений, связанных с ситуациями ожидания. Она помогает принять решение, устанавливающее определенное равновесие между размерами упущенной выгоды (доходов) и величиной дополнительных затрат в сервисных организациях. Например, такие как банки, магазины, железнодорожные и авиационные кассы, поликлиники, автозаправочные станции, ремонтные фирмы, парикмахерские, телефонные станции и другие. Клиенты, не желающие стоять в очереди, представляют упущенную выгоду. Время ожидания можно сократить за счет увеличения количества операторов, обслуживающих систему, что ведет к увеличению затрат. В основе расчетов лежит известная формула Пуассона:

 

 

                                            (4.2.3)

 

где P_n – вероятность появления n-го количества клиентов; e – основание натурального логарифма, е = 2,7183…; λ – среднее количество клиентов; n –количество клиентов в единицу времени.

Основными характеристиками модели теории очередей являются количество каналов обслуживания, среднее время обслуживание одного клиента, количество клиентов, время ожидания обслуживания и др. На основе выполненных расчетов определяется необходимое количество каналов обслуживания при допустимом, с точки зрения клиента ожидании обслуживания.

в) Теория запасов была разработана в начале ХХ столетия, а широкое применение началось с 40-х годов. Наибольших успехов, как правило, достигали японские предприятия. Использование теории запасов позволяет установить равновесие между затратами на создание запасов и издержками, связанными с потерями в случае нарушения производственного процесса. Запасы называют «бездействующими ресурсами» (idle resource), они подвержены порче, хищениям, устареванию и прочее, кроме того, они увеличивают расходы на оборотные средства предприятия. Теория запасов позволяет определить экономически выгодный размер запаса (economic order quantity – EOQ) по формуле, разработанной Гаррисоном Ф. В 1915 г.

 

 

                                                                            (4.2.4)

 

 

где Q – экономически выгодный размер запаса; O – затраты на оформление заказа (order cost); D – годовые запасы; H – издержки хранения (holding cost); i – начисления к стоимости хранящихся запасов (определяется как отношение дохода, которого можно было бы получить от вложения капитала на другие цели к величине стоимости запасов); P – стоимость хранящихся запасов (price).

EOQ является таким количеством запаса, который позволяет свести к минимуму общие издержки, связанные с хранением запаса.

г) Экономический анализ оперирует такими известными понятиями, как постоянные и переменные издержки, выручка от реализации, цена за единицу продукции, минимальный объем реализации или точка безубыточности, порог рентабельности, запас финансовой прочности, сила операционного (производственного) рычага и др.

 

Qmin = FC / (P - VC)          (4.2.5)

 

где Q_min минимальный объем реализации (точка безубыточности); F_c – постоянные издержки; P – цена единицы продукции; V_c – переменные издержки на единицу продукции.

Перечисленные понятия используются для моделирования ситуаций типа, что будет с прибылью, если изменятся объем продаж, издержки, цена и др.

Определение точки безубыточности может проводиться графическим путем, как показано на рис. 14.

 

 

Рис. 14. График определения точки безубыточности

 

Крутизна наклона кривой валовых поступлений зависит от цены товара. При увеличении фирмой цены товара наклон кривой валовых издержек становится более крутым и соответственно фирма может сократить объем продаж, сохранив целевую прибыль.

Условие безубыточности:

TC = TR.

 

TC = FC + VC * N = P * Qmin,

 

отсюда можем найти Qmin.

 

Qmin = FC / (P - VC)

 

где TC – общие издержки;

TR – объем продаж.

Соответственно цена изделия в точке безубыточности может быть рассчитана следующим образом:

P = FC / Qmin + VC.

 

4. Методы прогнозирования используются для предвидения изменений и последствий влияния внешней и внутренней среды на организацию и подразделяются на:

а) качественные

б) количественные.

а) К качественным методам прогнозирования относятся в основном методы предвидения спроса, такие как мнение потребителей, мнение покупателей, мнение опытных менеджеров, рыночные тесты. С помощью этих методов определяют, как изменится объем и структура продаж в зависимости от цены товара, местонахождения и уровня доходов клиентов и других факторов.

б) Основными методами прогнозирования являются известные методы количественных ассоциативных оценок (построение статистических прогнозов на основе временных рядов, корреляционного и регрессионного анализов и др.).

К количественным методам прогнозирования относят анализ временных рядов (АВР) и корреляционно-регрессионный анализ (КРА).

· АВР позволяет сделать выводы о текущем изменении показателей во времени. В прогнозных расчетах обычно используется следующая модель:

 

Y = f (T,C,S,R) (4.2.6)

 

где Y – прогнозируемый объект; T – основной тренд (тенденция); C – цикличность колебания вокруг тренда; S – сезонные колебания; R – необъясненные колебания (ошибки прогноза).

Прогнозирование на основе анализа временных рядов (АВР) использует методы экспоненциального сглаживания, экспоненциального сглаживания с учетом линейного тренда, экспоненциального сглаживания с учетом сезонной аддитивной компоненты.

Экспоненциальное сглаживание данных временного ряда основано на следующей зависимости:

P_i+1 = M_i

 

M_i = α X_i + (1 – α) M_i-1 (4.2.7)

 

где P_i+1 – прогноз;

M_i – экспоненциально сглаженное среднее в период i;

X_i – исходный временной ряд;

α – параметр сглаживания (0 ≤ α ≤ 1).

Экспоненциальное сглаживание с учетом линейного тренда использует следующие соотношения:

          P_i+1 = M_i + Т_i            (4.2.8)

 

где M_i = α X_i + (1 – α) M_i-1 + Т_i-1 

Т_i = γΔM_i + (1 – γ) Т_i-1 

ΔM_i = M_i – M_i-1

T_i – экспоненциально сглаженное значение тренда;

ΔM_i – оценка величины тренда в i-м периоде.

 

Экспоненциальное сглаживание с учетом сезонной аддитивной компоненты основано на расчете по следующим формулам:

 

P_i+1 = M_i + В_i+d                                (4.2.9)

 

где M_i = α X_i + (1 – α) M_i-1 

B_i = B_i-1 + (1 – β) e_i 

d – сезонный лаг;

e – ошибка прогноза в текущий момент времени, которая определяется как разность между фактом и прогнозом данных в период i;

B_i – величина сезонной компоненты.

· Метод корреляционно-регрессионного анализа (КРА) построен на использовании моделей причинного прогнозирования, которые содержат ряд переменных, имеющих отношениек предсказываемой переменной.

В основе корреляционного анализа лежит расчет коэффициентов корреляции –  +1 ≥ r ≥ -1. Эти коэффициенты показывают степень, или силу линейной взаимосвязи.

 

 

(4.2.10)

 

 

После определения связи между этими переменными строится статистическая модель, которая и используется для прогноза.

· Наиболее часто используемой количественной моделью является модель линейного регрессионного анализа.

 

           y = a₀ + a₁x    (4.2.11)

 

где y – значение независимой переменной; a₁ – коэффициент, определяющий угол наклона прямой; a₀ – отрезок, отсекаемый прямой на оси у; x – независимая переменная.

Основным методом расчета зависимой переменной y является метод наименьших квадратов (МНК). Так, если анализ эмпирических данных показывает, что основная тенденция выражается прямолинейно, то можно воспользоваться уравнением прямой линии;

 

y = a₀ + a₁x               (4.2.12)

 

где – y является прогнозируемой величиной объема в зависимости от времени x. Задача состоит в определении коэффициентов a₀ + a₁.

Для определения коэффициентов a₀ + a₁ составляют систему нормальных уравнений:

 

∑ y_i = Na₀ + a₁∑ x_i    (4.2.13)

 

∑ x_i y_i = a₀ ∑ x_i + a₁∑ x_i²     

 

Решив эту систему уравнений, получим значения коэффициентов:

 

(4.2.14)

 

Для определения точности регрессионных оценок рассчитывают стандартную ошибку прогноза S_y,x. Ее называют стандартным отклонением уравнения регрессии:

 

(4.2.15)

 

 

где Y_i – значение функции в i-й точке;

Y_c – расчетное значение зависимой переменной уравнения регрессии;

n – число точек данных.

Множественный регрессионный анализ использует расширенное представление линейной зависимости как функцию нескольких переменных:

 

y = a₀ + a₁x₁ + a₂x₂      (4.2.16)

 

Для вычисления множественной регрессии чаще всего применяются компьютерные программы, реализующие формулы, которые подробно описаны в учебниках по статистике. Которые подробно изучаются в таких дисциплинах как «Теория вероятности и математическая статистика», «Общая теория статистики» и др.