
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Положение второе: так как электрическая дуга представляет собой проводник с током, то при ее взаимодействии с внешним магнитным полем, появляется сила, заставляющая дугу перемещаться.⇐ ПредыдущаяСтр 12 из 12
Но и при отсутствии специальной системы электродинамические силы способствуют гашению дуги. Контур тока, изображенный на рис. 2.4.9 образует виток, на проводник которого, как показал третий пример, действует сила, стремящаяся увеличить диаметр витка. Благодаря этому опорные точки дуги интенсивно перемещаются с контактов на дугогасительные рога, предотвращая выгорание контактов. Происходящее при этом вытягиваниедуги приводит к увеличению падения действующие на ней, что также способствует гашению.
КОНТРОЛЬНОЕ ЗАДАНИЕ Общие указания 1. Для контроля приобретенных знаний предлагается решить двенадцать задач на следующие темы: "Основы тепловых расчетов", "Основы электродинамических расчетов", "Расчет электромагнита". Вариант контрольной работы выбирается из табл. 3.1.1 по двум последним цифрам номера зачетной книжки. Таблица 3.1.1 Варианты задания Предпоследняя цифра шифра |
Последняя цифра шифра | ||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |||||
| Номера вариантов | ||||||||||||||
| 0 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | ||||
| 1 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 | ||||
| 2 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 | 4 | 5 | ||||
| 3 | 8 | 9 | 10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||
| 4 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
| 5 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | ||||
| б | 5 | 6 | 7 | 8 | 9 | 10 | 1 | 2 | 3 | 4 | ||||
| 7 | 7 | 8 | 9 | 10 | 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 8 | 9 | 10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 9 | 10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
|
|
2. Контрольная работа выполняется в отдельной тетради, на обложке которой должны быть указаны фамилия, имя, отчество студента, шифр, номер варианта.
3. Текст, формулы и числовые расчеты должны быть написаны аккуратно, без помарок. Схемы, графики и диаграммы выполняются с помощью чертежных инструментов.
4. Каждое вычисление при решении задачи должно сопровождаться соответствующим объяснением.
5. Ошибки, обнаруженные преподавателем, исправляются в той же тетради, после решения. Не разрешается исправлять текст, расчеты и графики, уже рассмотренные рецензентом. При отсутствии места в тетради следует подклеить к ней дополнительные листы.
Задачи
Задача 1. Алюминиевая шина прямоугольного сечения нагружена переменным током I с частотой f. Размеры сечения шины - h ×ẟ, коэффициент поверхностного эффекта – k п. До какой температуры нагрета шина? Какова мощность потерь в 1 м проводника?
Таблица 3.2.1
Данные для задачи 1
| Величина
| Вариант | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| h, мм | 100 | 100 | 100 | 120 | 120 | 130 | 80 | 90 | 95 | 125 |
| ẟ, мм | 10 | 15 | 10 | 10 | 12 | 12,5 | 10 | 12 | 11 | 12 |
| I, А | 1800 | 1400 | 1500 | 1800 | 1600 | 2000 | 1800 | 1500 | 1600 | 1500 |
| f,Гц | 250 | 200 | 150 | 150 | 200 | 200 | 250 | 200 | 100 | 100 |
| k п | 1,4 | 1,4 | 1,25 | 1,2 | 1,45 | 1,45 | 1,35 | 1,4 | 1,15 | 1,25 |
Задача 2. Алюминиевые шины прямоугольного сечения расположены в параллельных плоскостях на расстоянии а друг от друга и нагружены переменным током I с частотой f. Размеры сечения шин - h ×ẟ, температура шин — 80 °С. Какова мощность потерь в 1 м проводника? Какой должна быть величина постоянного тока, чтобы мощность потерь в 1 м проводника не превысила бы полученного значения?
Таблица 3.2.2
Данные для задачи 2
Величина
Вариант
Задача 3. Требуется подобрать такое значение длительного тока частотой 50 Гц, при котором мощность потерь в 100 м медного проводника, нагретого до температуры θ, не превысила Р. Тип и размеры проводника:
а) сплошной круглый проводник с диаметром сечения d 1;
|
|
б) труба с внешним диаметром d 2, и толщиной стенки ẟ2;
в) труба с внешним диаметром d 3 и толщиной стенки ẟ3;
г) труба с внешним диаметром d 4, и толщиной стенки ẟ4.
Таблица 3.2.3
Данные для задачи 3
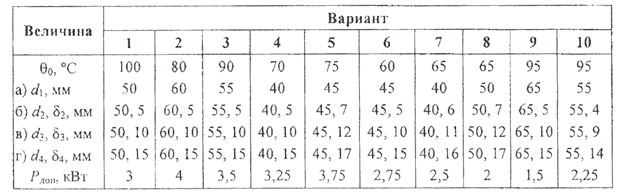
Задача 4. Одиночная медная шина имеет прямоугольное сечение с размерами h ×ẟ. Температура окружающей среды –θ0, допустимая температура нагрева проводника - θДОП. Коэффициент теплоотдачи k т= 15 Вт/(м2‧°С). Требуется определить время, в течение которого по шине может протекать а) постоянный ток I; б) переменный ток I частотой f= 50 Гц. При решении необходимо использовать уточненный метод расчета постоянной времени нагрева и установившегося изменения температуры.
Таблица 3.2.4
Данные для задачи 4
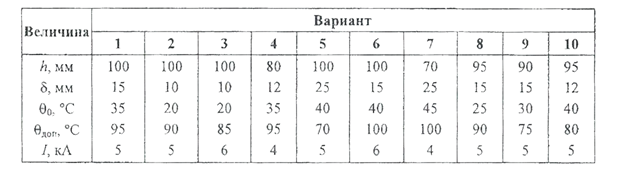
Задача 5. Одиночная медная шина имеет прямоугольное сечение с размерами h ×ẟ. Температура окружающей среды –θ0. Коэффициент теплоотдачи k т=15 Вт/(м2‧ °С). До какой температуры нагреется шина, если по ней будет протекать постоянный ток величиной I с продолжительностью включения ɛ (время цикла составляет 10 мин)? Какова величина длительного переменного тока (f = 50 Гц), при которой шина нагреется до той же температуры, что и при постоянном токе? Задачу молено решать с использованием упрощенного метода расчета тепловой постоянной времени и установившегося перегрева.
Таблица 3.2.5
Данные для задачи 5
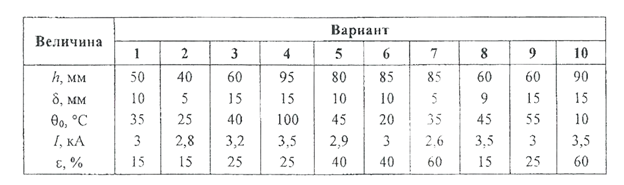
Задача 6. Одиночная алюминиевая шина имеет прямоугольное сечение с размерамиh ×ẟ. Температура окружающей среды –θ0. Коэффициент теплоотдачи k Т=12 Вт/(м2‧С). Требуется определить время, в течение которого по шине может протекать ток величиной I, не нагревая ее более θДОП. До какой температуры нагреется шина, если этот ток пропускать по ней в течение t p, а длительность паузы будет составлять t п? Задачу можно решать с использованием упрощенного метода расчета тепловой постоянной времени и установившегося перегрева.
Таблица 3.2.6
Данные для задачи 6
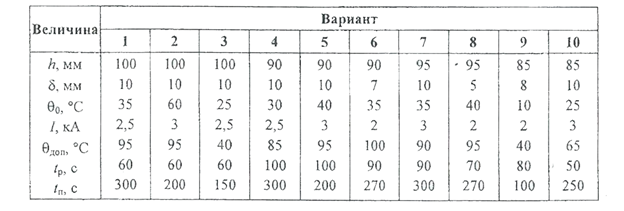
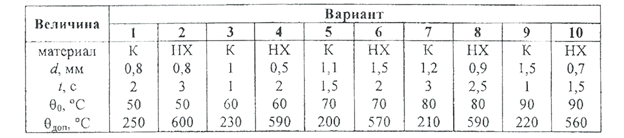
Задача 7. Диаметр поперечного сечения проволоки элемента сопротивления равен d. Требуется определить допустимую величину тока, протекающего по сопротивлению в течение времени t, если начальная температура элемента равна θ0, а допустимая температура –θдоп. Материал проволоки - константан (К) или нихром (НХ).
Таблица 3.2.7
Данные для задачи 7
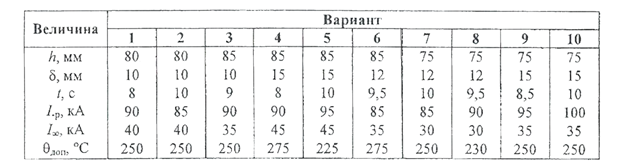
Задача 8. Ток короткого замыкания, протекающий по медной шине с размерами h ×ẟ в течение времени t, имеет следующие параметры: ударное значение I ~p, и установившееся значение I ∞. Какую температуру может иметь шина до режима короткого замыкания, если допустимая температура составляет θД0П?
Таблица 3.2.8
Данные для задачи 8
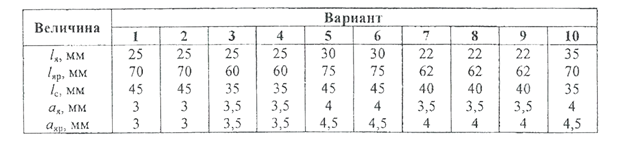
Задача 9. Геометрические размеры магнитопровода даны в соответствии с рисунком, приведенным в табл. 3.2.9. Толщина якоря - b я, толщина ярма - b яр. Заданы марка стали и начальный воздушный зазор - ẟтрог. Требуется определить магнитодвижущую силу катушки электромагнита, необходимую для создания электромагнитной силы трогания F трог.
Таблица 3.2.9
Данные для задачи 9
Окончание табл. 3.2.9
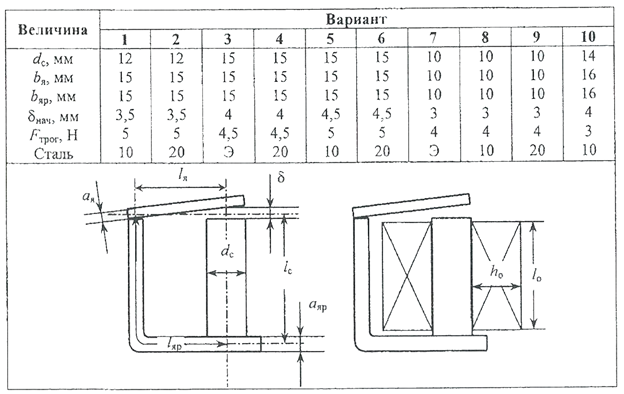
Задача 10. Магнитодвижущая сила бескаркасной обмотки, расположенной на сердечнике электромагнита (рис. табл. 3.2.9) равна I ‧ w, напряжение питания - U, геометрические размеры окна катушки - h o× l o. Обмотка нагрета до температуры θ. Необходимые геометрические размеры магнитопровода - взять из предыдущего примера. Требуется рассчитать параметры обмотки: диаметр обмоточного провода d, число витков w, сопротивление R, потребляемый ток I и тепловые потери мощности Р.
|
|
Таблица 3.2.10
Данные для задачи 10
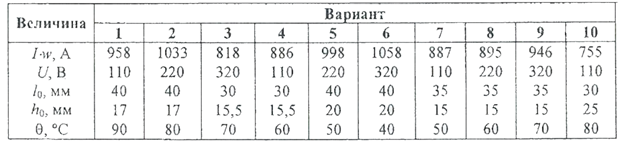
Задача 11. При срабатывании электромагнита, параметры которого были заданы и рассчитаны в предыдущих примерах, воздушный зазор между якорем и сердечником уменьшается до ẟкон. Требуется определить силу удержания якоря в притянутом состоянии. (Ток и число витков катушки электромагнита необходимо взять из предыдущего примера.)
Таблица 3.2.11
Данные для задачи 11

Задача 12. Какова сила, действующая на участок проводника длиной а, расположенный под углом 90° к другому участку проводника длиной h. Диаметр сечения проводника - d, ток проводника - I.
Таблица 3.2.12
Данные для задачи 12

ПРИЛОЖЕНИЕ
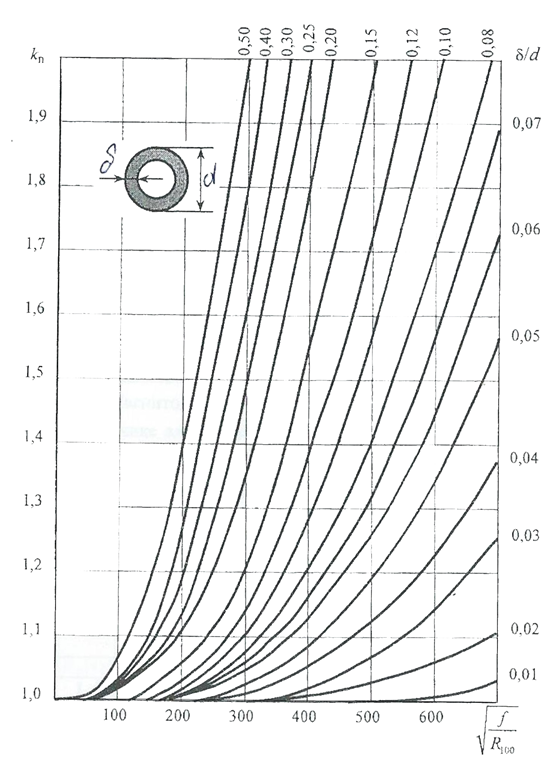
Рис. П. 1. Зависимость коэффициента поверхностного эффектадля сплошных и полых трубчатых проводников из немагнитного материалас различным соотношением ẟ/ d, от параметра 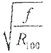
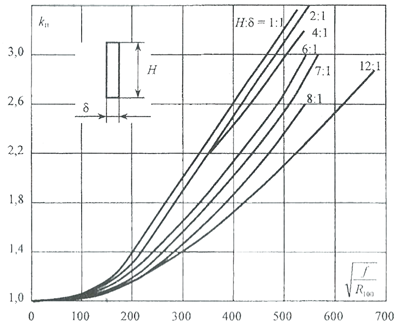
Рис. П.2. Зависимость коэффициента поверхностного эффекта для прямоугольных проводников из немагнитного материалас различным соотношением h / ẟ от параметра 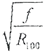
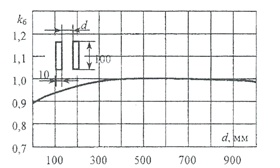
Рис. П.З, Зависимостькоэффициента близостиот расстояния между двумяпараллельными шинами,расположеннымив параллельных плоскостях
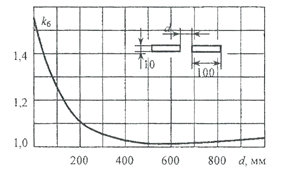
Рис. П.4. Зависимостькоэффициента близостиот расстояния между двумяпараллельными шинами,расположеннымив одной плоскости
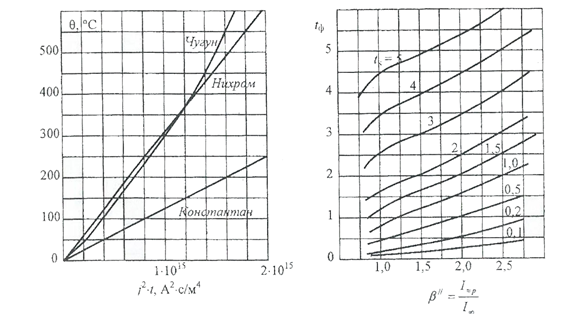
Рис. П.5. Кривые адиабатическогоРис. П.6. Зависимость фиктивного
нагрева реостатных материалов времени короткого замыканияот
параметра β//
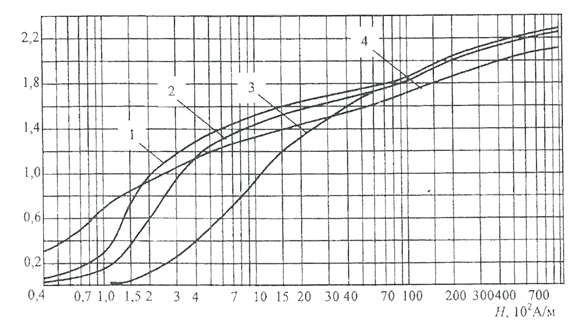
Рис. П.7. Кривые намагничивания магнитных материалов:
1 - сталь низкоуглеродистая электротехническая марки Э отожженная;
2 - сталь качественная конструкционная марки сталь 10 отожженная;
3 - сталь качественная конструкционная марки сталь 20 отожженная;
4 - сталь листовая электротехническая марки Э41
Таблица П.1
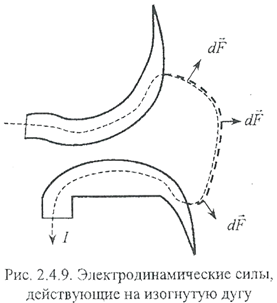 Таким образом, полученное в третьем разобранном примере мизерное значение электродинамического усилия 4,037‧10-3Н не должно рассматриваться нами как незначительное, поскольку в определенных обстоятельствах даже такое усилие может произвести значительный эффект. Дуга - очень легкий проводник, поэтому для ее перемещения в дугогасительную камеру достаточно создать силу, соответствующую легкому дуновению ветра. Не случайно система гашения дуги в магнитном поле имеет еще одно название - "магнитное дутье".
Таким образом, полученное в третьем разобранном примере мизерное значение электродинамического усилия 4,037‧10-3Н не должно рассматриваться нами как незначительное, поскольку в определенных обстоятельствах даже такое усилие может произвести значительный эффект. Дуга - очень легкий проводник, поэтому для ее перемещения в дугогасительную камеру достаточно создать силу, соответствующую легкому дуновению ветра. Не случайно система гашения дуги в магнитном поле имеет еще одно название - "магнитное дутье". 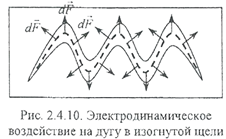 В дугогасительной камере с изогнутой щелью наблюдается аналогичная картина. Из второго примера следует, что при изгибе проводника возникает электродинамическая сила, стремящаяся выпрямить проводник. На рис. 2.4.10.показано, что на каждый изгиб дуги действует сила, прижимающая дугу к стенке камеры. Более тесный контакт с материалом дугогасительной камеры способствует охлаждению и гашению дуги.
В дугогасительной камере с изогнутой щелью наблюдается аналогичная картина. Из второго примера следует, что при изгибе проводника возникает электродинамическая сила, стремящаяся выпрямить проводник. На рис. 2.4.10.показано, что на каждый изгиб дуги действует сила, прижимающая дугу к стенке камеры. Более тесный контакт с материалом дугогасительной камеры способствует охлаждению и гашению дуги.


