
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Положение второе: эффект близости может, как усугублять поверхностный эффект, так и компенсировать его.
При формальном выполнении расчетов тепловых потерь в проводниках с переменным током, без учета физической сущности явлений, лежащих в основе коэффициентов kп и kб, возможно получение результата, противоречащего здравому смыслу. Например, если во втором рассмотренном примере (п.2.1.2) принять мощность потерь, равной 140 Вт, а толщину шины - 10 мм, величина Формально, задача решена правильно, но результат –kд = kп‧kб = 0,937 не соответствует природе рассматриваемых явлений. Коэффициент добавочных потерь kд меньше единицы означает, что активное сопротивление проводника переменному току меньше, чем постоянному. То есть элементарные токи распределились по сечению проводника равномерней, чем они распределяются при постоянном токе. Это физически невозможно. Чтобы избежать подобных ошибок, необходимо понимать, что эффект близости в предельном случае может свести коэффициент поверхностного эффекта к единице, но меньше единицы произведение этих коэффициентов быть не может. Тепловые режимы работы электрического аппарата Общие сведения Рассмотрим проводник с сопротивлением R и постоянным током I. За время t в этом проводнике выделится тепловая энергия
Одна часть этой энергии пойдет на изменение температуры проводника:
другая часть будет рассеиваться в окружающей среде:
В формулах (2.2.2) и (2.2.3) m - масса проводника, кг; с - удельная теплоемкость, Дж/(кг‧°С); τ- изменение температуры проводника или его перегрев, °С; k Т- коэффициент теплоотдачи, Вт/(°С‧м2); S - площадь поверхности охлаждения проводника. То есть, в каждый момент времени имеет место энергетический баланс: Поначалу первая часть суммы энергий больше второй и проводник интенсивно нагревается. Но по мере увеличения температуры проводника, тепло все более интенсивно рассеивается в окружающую среду. Через определенное время наступает состояние, при котором количество тепла, выделившееся в проводнике, становится равно энергии, передаваемой окружающей среде:
Из этого равенства можно получить изменение температуры, достигнутое ко времени наступления баланса (2.2.5). Этот перегрев называется установившимся:
Чтобы иметь возможность определять перегрев в любой момент времени на этапе нагрева проводника необходимо решить дифференциальное уравнение (2.2.4) относительно τ. Разделим левую и правую части уравнения на k Т‧ S п:
Решим уравнение (2.2.7) предварительно разделив переменные:
Решение уравнения с разделенными переменными имеет вид:
где τ0 и t 0 - начальные значения переменных. В общем случае проводник имеет некоторый начальный перегрев τ0. Процесс нагрева начинается с момента появления в проводнике тока, то есть в τ0 = 0. Принимая во внимание, что Первое слагаемое правой части выражения (2.2.8) описывает процесс охлаждения проводника с τ=τ0до τ=0 (кривая 1 на рис. 2.2.1):
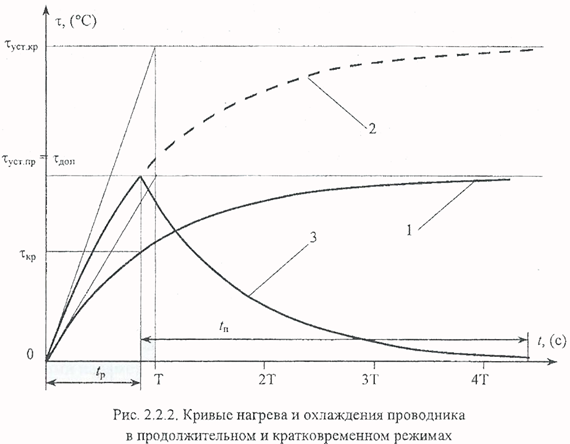
Второе слагаемое правой части выражения (2.2.8) описывает процесс нагрева проводника с τ=0до τ=τуст(кривая 2 на рисунке 2.1): Эти процессы происходят одновременно и их разделение на составляющие условно. Реальное изменение температуры происходит по кривой 3 рис.2.2.1. Рис. 2.2.1. Кривые нагрева и охлаждения проводника Из рис. 2.2.1 видно, что, если длительность периода нагрузки составляет около 4 Т, тепловой переходный процесс устанавливается. Режим работы проводника, при котором его температура достигает установившегося значения, называется продолжительным. Чтобы в этом режиме проводник не перегревался, установившийся перегрев не должен превышать допустимого значения. Для этого нормируют мощность тепловых потерь Рпр или ток I прпродолжительного режима.
Если время протекания тока I прменьше трех постоянных времени нагрева, а время бестоковой паузы в рабочем цикле проводника достаточно для его полного остывания, максимальный перегрев не будет достигать τдоп и проводник окажется недоиспользован по нагреву. На рис. 2.2.2 показано, что за время кратковременной работы с нагрузкой продолжительного режима (кривая 1 на рис. 2.2.2) температура проводника изменяется на τкр, что значительно меньше допустимой величины. Чтобы за время t р был достигнут перегрев τдоп, проводник должен нагреваться по кривой 2 (рис. 2.2.2). За время паузы температура снизится до температуры окружающей среды (кривая 3, рис. 2.2.2) и в следующем рабочем цикле нагрев начнется с τ = 0. Работая в таком режиме, проводник не будет перегреваться и будет полностью использован по нагреву.
Режим работы проводника, при котором за время токовой нагрузки температура не успевает достигнуть установившегося значения, а за время паузы снижается до температуры окружающей среды, называется кратковременным. Мощность тепловых потерь при нагреве по кривой 2 больше, чем при нагреве по кривой 1 (рис. 2.2.2). Если пренебречь зависимостью величины τуст от температуры, эти мощности будут соотноситься так же, как τуст.кр и τуст.пр. Таким образом, коэффициент перегрузки по мощности кратковременного режима равен:
Поскольку потери пропорциональны квадрату тока, коэффициент перегрузки по току кратковременного режима равен:
Если время паузы рассмотренного режима уменьшить настолько, что проводник не успеет остыть до окружающей температуры, тепловое состояние проводника существенно изменится. Нагрев в следующем рабочем цикле будет начинаться с τ> 0 и за время работы перегрев превысит допустимое значение. Такой режим, при котором ни за время работы, ни за время паузы температура проводника не успевает достигнуть установившегося значения, называется повторно-кратковременным. Для полного использования проводника по нагреву в этом режиме необходимо иметь формулы пересчета нагрузки повторно-кратковременного режима из нагрузки длительного и кратковременного режимов.
Коэффициент перегрузки по мощности повторно-кратковременного режима:
Коэффициент перегрузки по току повторно-кратковременного режима:
Необходимо помнить, что формулы (2.2.11)—(2.2.14) получены без учета зависимости τуст от температуры. Повторно-кратковременный режим характеризуется продолжительностью включения ПВ. Это доля времени работы в рабочем цикле, выраженная в процентах:
Существуют нормированные значения ПВ при нормированной длительности цикла, однако на практике реальные ПВ и длительность цикла работы проводника, как правило, не соответствуют норме. Но при всем многообразии необходимых пересчетов - из ПВ1, в ПВ2 при неизменном t ц, из t ц1 в t ц2 при неизменной ПВ, из кратковременного режима в повторно-кратковременный и обратно и т. д. - достаточно использования формул (2.2.12) и (2.2.14). Зная ток длительного режима по указанным формулам можно получить токи кратковременного и повторно-кратковременного режимов с любыми параметрами. А для любого непродолжительного режима можно вычислить эквивалентный ему ток длительного режима и на его основе сделать пересчет для тока непродолжительного режима с новыми параметрами.
Следующим важным режимом работы электрического аппарата или его отдельных деталей является режим короткого замыкания. Этот режим характеризуется большой токовой нагрузкой и малой длительностью. Ток в режиме короткого замыкания может в десять и более раз превышать номинальный ток проводника, а длительность режима составляет доли тепловой постоянной времени. То есть короткое замыкание (при правильной работе системы защиты) закапчивается в самом начале процесса нагрева, описываемого уравнением (2.2.4). Кривые нагрева в этот период времени представляют собой линии, почти совпадающие с касательными к ним (см. рис. 2.2.1-2.2.3). Такой нагрев можно считать адиабатическим, то есть происходящим без обмена теплом с окружающей средой. Если из уравнения энергетического баланса (2.2.4) исключить энергию, рассеиваемую в окружающую среду, получится уравнение баланса для адиабатического нагрева:
Преобразуя равенство (2.2.16), получим дифференциальное уравнение, которое после разделения переменных выглядит так:
Решив это уравнение относительно τ и перейдя от перегрева к температуре, получим выражение для определения температуры проводника при адиабатическом нагреве:
здесь γ - плотность материала проводника, кг/м3; j - плотность тока, А/м2. Величина j 2 ‧ t является мерой теплового воздействия тока на проводник. В функции этой величины принято строить кривые нагрева проводниковых материалов при коротких замыканиях. Эти кривые используются для упрощения вычислений при расчете деталей аппаратов на термическую устойчивость. Под термической устойчивостью понимают способность электрического аппарата противостоять термическому воздействию токов короткого замыкания. Поскольку температура проводника при адиабатическом нагреве определяется величиной j 2 ‧ t или (
Таблица 2.2.1
|
||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.013 с.) |
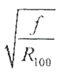 окажется равной 144. Этому значению соответствует коэффициент поверхностного эффекта kп=1,01, а коэффициент близостиkб, вычисленный по формуле (2.1.7) будет равен 0,928. По рисунку приложения П.4 можно определить расстояние между двумя шинами, расположенными в параллельных плоскостях: d=70 мм. Это и требовалось определить в задании.
окажется равной 144. Этому значению соответствует коэффициент поверхностного эффекта kп=1,01, а коэффициент близостиkб, вычисленный по формуле (2.1.7) будет равен 0,928. По рисунку приложения П.4 можно определить расстояние между двумя шинами, расположенными в параллельных плоскостях: d=70 мм. Это и требовалось определить в задании.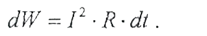 (2.2.1)
(2.2.1)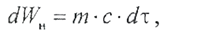 (2.2.2)
(2.2.2)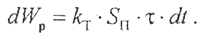 (2.2.3)
(2.2.3)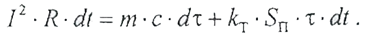 (2.2.4)
(2.2.4)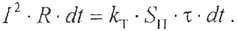 (2.2.5)
(2.2.5)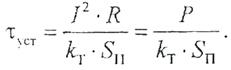 (2.2.6)
(2.2.6)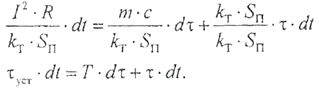 (2.2.7)
(2.2.7)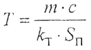 имеет размерность секунды и называется тепловой постоянной времени или постоянной времени нагрева. В числителе ее выражения находятся величины, характеризующие способность проводника накапливать тепло, а в знаменателе - величины, характеризующие его теплоотдающие свойства. Это значит, что чем больше постоянная времени нагрева, тем дольше происходит нагрев проводника и позднее начинается отдача всего выделяющегося в нем тепла в окружающую среду.
имеет размерность секунды и называется тепловой постоянной времени или постоянной времени нагрева. В числителе ее выражения находятся величины, характеризующие способность проводника накапливать тепло, а в знаменателе - величины, характеризующие его теплоотдающие свойства. Это значит, что чем больше постоянная времени нагрева, тем дольше происходит нагрев проводника и позднее начинается отдача всего выделяющегося в нем тепла в окружающую среду.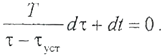
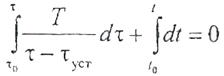
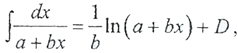 можем записать:
можем записать: 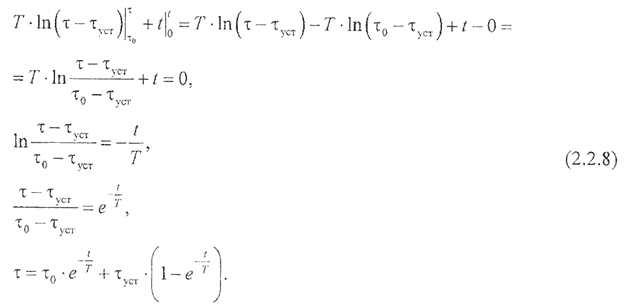
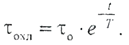 (2.2.9)
(2.2.9)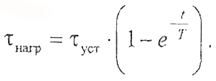 (2.2.10)
(2.2.10)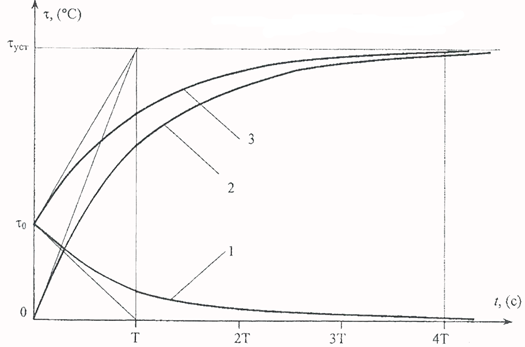
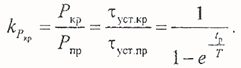 (2.2.11)
(2.2.11)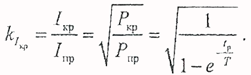 (2.2.12)
(2.2.12)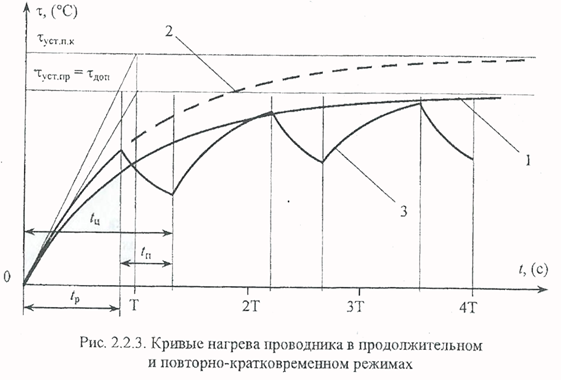
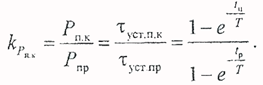 (2.2.13)
(2.2.13)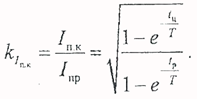 (2.2.14)
(2.2.14)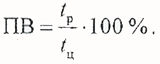 (2.2.15)
(2.2.15)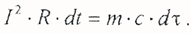 (2.2.16)
(2.2.16)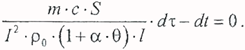
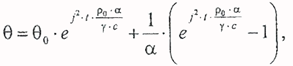 (2.2.17)
(2.2.17)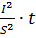 ), термическую устойчивость нормируют током термической устойчивости и длительностью протекания этого тока. Нормированное время термической устойчивости - 10, 5, 1 и 0,5 с. Ток термической устойчивости аппарата определяется его конструкцией и используемыми при его изготовлении материалами. Для отдельного сплошного проводника этот ток может быть определен по предельной для каждого t т.у. плотности тока (табл. 2.2.1). Нетрудно убедиться, что величина j 2 ‧ t для каждого столбца таблицы остается неизменной.
), термическую устойчивость нормируют током термической устойчивости и длительностью протекания этого тока. Нормированное время термической устойчивости - 10, 5, 1 и 0,5 с. Ток термической устойчивости аппарата определяется его конструкцией и используемыми при его изготовлении материалами. Для отдельного сплошного проводника этот ток может быть определен по предельной для каждого t т.у. плотности тока (табл. 2.2.1). Нетрудно убедиться, что величина j 2 ‧ t для каждого столбца таблицы остается неизменной.


