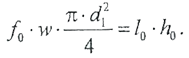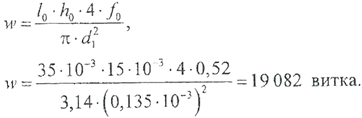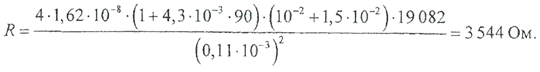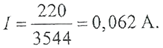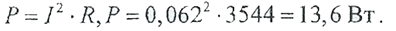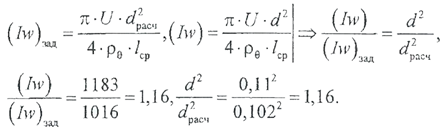Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Данные для построения вебер-амперной характеристикиСодержание книги
Поиск на нашем сайте
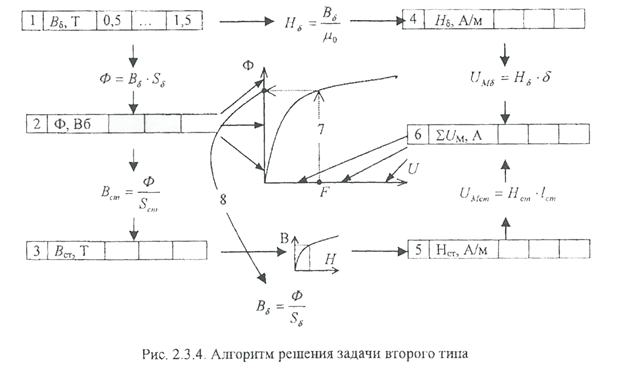
На первом этапе расчета, задаются значениями индукции в зазоре. Максимальное значение магнитной индукции должно быть соотнесено с конкретными условиями задачи. При недостатке опыта расчетов можно выбрать значение 1,5 T. Таким образом заполняется первая строка таблицы. Далее, для выбранных значений индукции, но формуле (2.3.4) рассчитывают значения магнитного потока и заполняют вторую строку таблицы. Ф = B ẟ ‧S ẟ. По полученным значениям потока находят индукцию в остальных участках магнитопровода. В нашем случае это единственный, стальной участок.
Полученными значениями индукции заполняется третья строка. Напряженность магнитного поля в воздушном зазоре (четвертая строка) находится с использованием формулы (2.3.2), напряженность в стали (пятая строка) - по кривой намагничивания. Последняя строка таблицы заполняется значениями суммы падений магнитного напряжения на всех участках магнитопровода. В рассматриваемой задаче это
Вебср-амперную характеристику строят, откладывая по оси абсцисс значения магнитного напряжения, а по оси ординат - значения потока. Полученный график функции Ф = f (U M) позволяет определять значение магнитного потока в контуре для любого значения магнитодвижущей силы, в том числе и для заданного. После этого, но формуле (2.3.4) находят индукцию в зазоре при заданном значении МДС. Рассмотренный алгоритм решения задачи схематично представлен на рис. 2.3.4.
Примеры решения задач
Решение. При составлении схемы замещения, представленной на рис. 2.3.6, были сделаны следующие допущения: весь магнитный поток сосредоточен в магнитопроводе, воздушный зазор в месте соединения якоря с ярмом отсутствует.
где F — сила тяги электромагнита, Н; S ẟ - площадь поперечного сечения воздушного промежутка, м2. Если пренебречь искривлением магнитных линий в воздушном промежутке, поперечное сечение зазора можно принять равным поперечному сечению сердечника. Выразив из формулы (2.3.8) магнитный поток, найдем его значение.
В соответствии с алгоритмом решения, представленном на рис. 2.3.4, следующим шагом должно быть определение магнитной индукции, но пред-варительно необходимо вычислить площади сечения участков магнитопровода. Площадь поперечного сечения якоря, ярма и сердечника:
Магнитная индукция в якоре, ярме, сердечнике и зазоре:
Напряженность магнитного поля в зазоре определяется по аналитической зависимости (2.3.2), в стальных участках – графически, с использованием кривой намагничивания для стали 20 (рис. П.7).
Анализируя полученный результат, можно сделать важный вывод: напряженность магнитного ноля в зазоре на несколько порядков выше, чем в стальных участках. И дальнейшие расчеты покажут, что, из-за очень большого магнитного сопротивления воздушного промежутка, на него будет приходиться почти все падение магнитного напряжения контура. Магнитное напряжение на участках магнитопровода определяем по формуле (2.3.6):
Сумма магнитных напряжений есть магнитодвижущая сила, необходимая для создания требуемого по условию задачи тягового усилия.
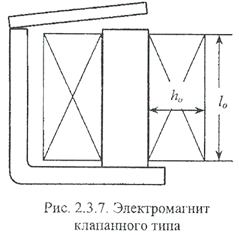
Ответ: I w = 1 016 А. Пример 2. Магнитодвижущая сила бескаркасной обмотки, расположенной на сердечнике электромагнита (рис. 2.3.7) равна F = 1016 А, напряжение питания U = 220 В, геометрические размеры: h 0 = 15 мм, l 0 - 35 мм. Необходимые геометрические размеры магнитопровода - взять из предыдущего примера. Обмотка нагрета до температуры 90 °С. Необходимо рассчитать параметры обмотки: диаметр обмоточного провода d, число витков w, сопротивление R, потребляемый ток I и тепловые потери мощности Р.
После преобразования получим
где ρ0 - удельное сопротивление проводника при температуре 0 °С, Ом‧м; α- температурный коэффициент сопротивления, 1/°С; θ - температура, °С; l ср - средняя длина витка обмотки, м. Средняя длина витка:
Подставив (2.3.10) в (2.3.9), получим окончательное выражение для диаметра обмоточного провода. Нужно понимать, что на данном этапе решения задачи вычисляется расчетное значение диаметра провода. Реальное значение определяется существующей номенклатурой обмоточных материалов. Исходя из этого, к обозначению диаметра добавим соответствующий индекс:
Обмоточный провод изготавливают из меди, поэтому удельное сопротивление и температурный коэффициент сопротивления выбираем для этого материала: ρ0=1,62‧10-8Ом‧м, α = 4,3 ‧ 10-31/°С.
После преобразований получаем формулу для определения числа витков обмотки электромагнита и производим расчет:
(2.3.13)
Электрическое сопротивление обмотки можно вычислить с помощью формулы (2.3.9): Ток, потребляемый обмоткой, определяется по закону Ома:
Выделяющаяся в катушке мощность тепловых потерь:
На завершающей стадии расчетов, после многочисленных преобразований формул и математических вычислений необходимо оценить полученные результаты с точки зрения их реалистичности. В качестве проверки правильности расчетов целесообразно вычислить магнитодвижущую силу получившейся катушки и сравнить ее с заданным значением: I w = 0,062‧3544 = 1183 А. Полученное значение больше заданного, но этот результат объясним: выбранный обмоточный провод имел диаметр больше расчетного, а несложные расчеты показывают, что полученное и заданное значения магнитодвижущей силы соотносятся так же, как вторые степени выбранного и расчетного диаметров обмоточного провода.
Таким образом, проверка подтвердила правильность решения задачи. Ответ: d = 0,11 ‧10-3м2, w = 19082,R= 3544 Ом, I = 62‧10-3 A, P = 13,6 Вт. Пример 3. При срабатывании электромагнита, параметры которого были заданы и рассчитаны в предыдущих примерах, воздушный зазор между якорем и сердечником уменьшается до ẟКOН = 0,1 мм. Определить силу удержания якоря в притянутом состоянии. Данный пример относится ко второму типу задач на расчет магнитных цепей (см. п. 2.3.1). Схема замещения рассматриваемой в примере магнитной цепи представлена на рис. (2.3.1.б). В соответствии с алгоритмом, представленным на рис. 2.3.4, в первую очередь необходимо задаться значениями индукции в воздушном зазоре.
Значениями от 0,4 T до 1,2 T заполним первую строку табл. 2.3.2. Таблица 2.3.2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.76.250 (0.011 с.) |

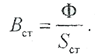
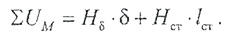
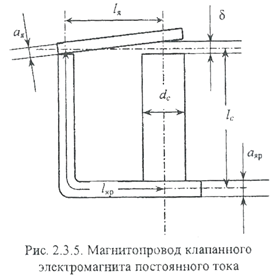 Пример 1. Определить магнитодвижущую силу трогания электромагнита, изображенного на рис. 2.3.5, необходимую для создания при начальном рабочем зазоре ẟтрог = 3 мм электромагнитной силы трогания F трог= 5 Н. Материал магнитопровода - сталь 20. Геометрические размеры магнитопровода: длина якоря l я= 22 мм, длина ярма l яр = 62 мм, длина сердечника l с = 40 мм, толщина якоря ая = 3 мм, толщина ярма а яр = 4 мм, диаметр сердечника d c= 10 мм, ширина якоря и ярма (на рисунке не показаны) bя=bяр=15 мм.
Пример 1. Определить магнитодвижущую силу трогания электромагнита, изображенного на рис. 2.3.5, необходимую для создания при начальном рабочем зазоре ẟтрог = 3 мм электромагнитной силы трогания F трог= 5 Н. Материал магнитопровода - сталь 20. Геометрические размеры магнитопровода: длина якоря l я= 22 мм, длина ярма l яр = 62 мм, длина сердечника l с = 40 мм, толщина якоря ая = 3 мм, толщина ярма а яр = 4 мм, диаметр сердечника d c= 10 мм, ширина якоря и ярма (на рисунке не показаны) bя=bяр=15 мм. 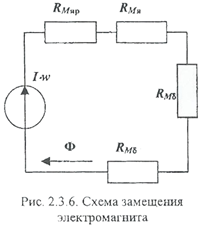 В рассматриваемом примере нетрудно видеть признаки задачи первого типа: магнитный поток можно считать известным, поскольку сила тяги электромагнита связана с ним следующим выражением.
В рассматриваемом примере нетрудно видеть признаки задачи первого типа: магнитный поток можно считать известным, поскольку сила тяги электромагнита связана с ним следующим выражением.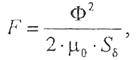 (2.3.8)
(2.3.8)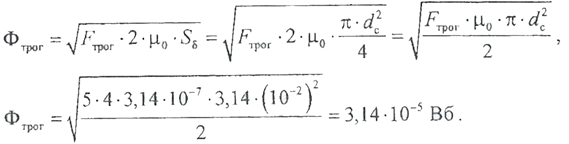
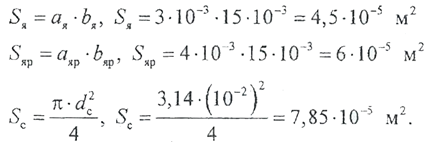
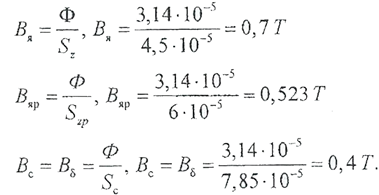

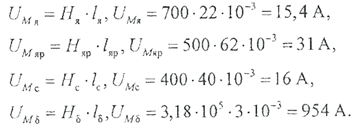
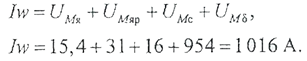
 Решение. Выражение для определения диаметра обмоточного провода можно получить, приравняв две формулы электрического сопротивления:
Решение. Выражение для определения диаметра обмоточного провода можно получить, приравняв две формулы электрического сопротивления: 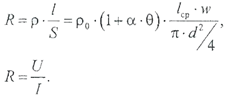 (2.3.9)
(2.3.9)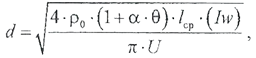 (2.3.10)
(2.3.10)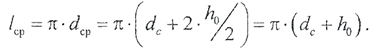 (23.11)
(23.11)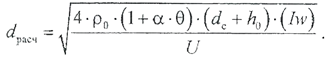 (2.3.12)
(2.3.12)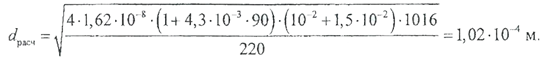
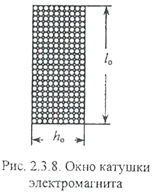 По таблице приложения П.1 выбираем провод марки ПЭВ-1 со следующими данными: диаметр провода без изоляции d =0,11‧10-3 м2, диаметр провода с изоляцией d 1=0135‧10-3м2,коэффициентзаполнения, характеризующий плотность укладки провода в катушке f 0=0,52. Изолированный провод с диаметром d 1 должен заполнить окно катушки с размерами l 0× h 0. Количество круглых сечений проводника, поместившихся в окне катушки, будет равно искомому числу витков (рис. 2.3.8). Учитывая коэффициент заполнения, приравниваем площадь, занимаемую круглыми сечениями и площадь прямоугольного окна:
По таблице приложения П.1 выбираем провод марки ПЭВ-1 со следующими данными: диаметр провода без изоляции d =0,11‧10-3 м2, диаметр провода с изоляцией d 1=0135‧10-3м2,коэффициентзаполнения, характеризующий плотность укладки провода в катушке f 0=0,52. Изолированный провод с диаметром d 1 должен заполнить окно катушки с размерами l 0× h 0. Количество круглых сечений проводника, поместившихся в окне катушки, будет равно искомому числу витков (рис. 2.3.8). Учитывая коэффициент заполнения, приравниваем площадь, занимаемую круглыми сечениями и площадь прямоугольного окна: