
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цепи переменного тока с ферромагнитными элементамиСодержание книги
Поиск на нашем сайте
Глава 6а ЦЕПИ ПЕРЕМЕННОГО ТОКА С ФЕРРОМАГНИТНЫМИ ЭЛЕМЕНТАМИ
КАТУШКА С МАГНИТОПРОВОДОМ
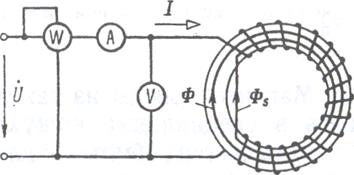
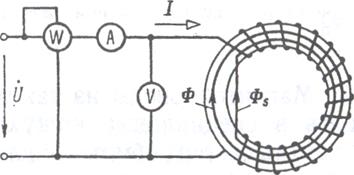
Основные параметры ферромагнитного материала определяют в результате экспериментального исследования катушки с магнитопроводом из однородного ферромагнитного материала, одинакового поперечного сечения, без воздушного зазора. Для такого исследования предпочтительна тороидальная форма магнитопровода, так как при этом обеспечиваются наиболее точные измерения. С помощью приборов, показанных на схеме рисунок 6.2, можно определить основные параметры характеристики ферромагнитного материала.
Рисунок 6.2. Схема для приближенного определения параметров катушки с ферромагнитным магнитопроводом при переменном токе в обмотке.
При исследовании обычно известны число витков обмотки до, активное сопротивление обмотки г, сечение магнитопровода SCT, длина средней линии напряженности поля l ср и частота f. По показаниям электроизмерительных приборов определяют ток I, напряжение U на выводах обмотки и потребляемую мощность Р (при определении Р из показания ваттметра необходимо вычесть мощности потерь в амперметре и вольтметре). Действующая напряженность Н магнитного поля определяется по формуле:
При синусоидальном напряжении амплитуда магнитного потока, замыкающегося по магнитопроводу катушки:
где Е - действующая э. д. с., наводимая в обмотке вышеуказанным магнитным потоком. Кроме магнитного потока Ф, замыкающегося по магнитопроводу катушки, имеется еще магнитный поток рассеяния Ф S, замыкающийся через воздух и показанный на рисунке 6.2 условно (поток рассеяния может быть сцеплен лишь с частью витков обмотки). Так как магнитное сопротивление воздуха значительно больше магнитного сопротивления магнитопровода, поток Ф S можно считать совпадающим по фазе с током и прямо пропорциональным ему Это дает возможность учитывать э. д. с., наводимую потоком рассеяния, с помощью сопротивления рассеяния xS '. Так как положительные направления тока и наведенной потоком Ф S э. д. с. совпадают, то сумма приложенного напряжения и наведенной э. д. с. равна падению напряжения в активном сопротивлении и сопротивлении рассеяния:
Откуда:
В большинстве случаев Е мало отличается от U. Амплитуда магнитной индукции:
Разность между мощностью, потребляемой катушкой, и мощностью, затрачиваемой на нагрев обмотки, равна потерям мощности в стали магнитопровода:
Удельные потери в стали:
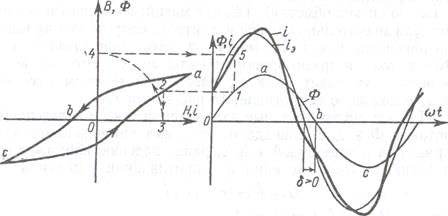
где γ CT - плотность материала магнитопровода. Для катушки с магнитопроводом характерными являются два режима работы: 1.напряжение на выводах обмотки синусоидально, а ток в обмотке несинусоидален; 2.ток в обмотке синусоидален, а напряжение на выводах несинусоидально. В первом случае при r ≈ 0 можно принять магнитный поток синусоидальным и построить кривую тока i (t). Порядок построения кривой i (t) показан на рисунке 6.3. На кривой магнитного потока Ф(t) произвольно выбирается точка посредством горизонтальной линии 1-2, пересекающей кривую Ф (t), и вертикальной линии 2- 3 определяется значение тока i, равное абсциссе 0-3 и соответствующее значению (ординате) потока в точке 1; это значение тока откладывается в виде ординаты 0-4 и переносится в координатную систему i (t) посредством проведения горизонталь ной линии 6.5 до пересечения с вертикальной прямой 1- 5. При выборе исходных точек на нисходящей части кривой abc значение тока i определяется также по нисходящей ветви abc петли Ф (t).
Рисунок 6.3. Графическое определение тока в катушке при синусоидальном магнитном потоке.
Изображенная на рисунке 6.3 кривая i (t) симметрична относительно оси абсцисс, что означает отсутствие четных гармоник. Эквивалентная синусоида тока i сдвинута по фазе относительно магнитного потока Ф на угол δ. При синусоидальном приложенном напряжении э. д. с., наводимая в обмотке, несинусоидальна вследствие появления высших гармонических составляющих в токе. Однако искажение э. д. с. обычно незначительно и, представляя ее в виде эквивалентной синусоиды, можно принять - где U ф - составляющая приложенного напряжения Отношение:
- комплексная проводимость ветвей намагничивания и потерь в стали; у0 - полная проводимость ветвей намагничивания и потерь в стали:
где g 0 - проводимость ветви потерь в стали; b - проводимость ветви намагничивания. Иногда в расчетах применяется комплексное сопротивление ветвей намагничивания и потерь в стали:
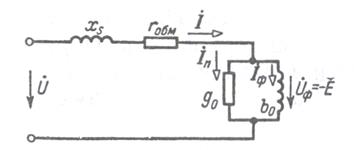
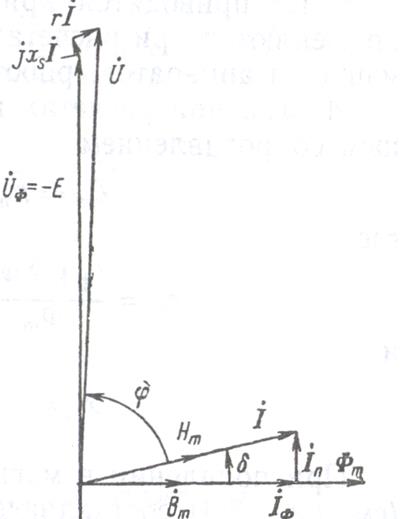
Ток в обмотке представляется в виде двух составляющих: намагничивающего тока В соответствии со сказанным изображаются схемы замещения (рисунок 6.4) и векторная диаграмма (рисунок 6.5) катушки с магнитопро- водом.
Рисунок 6.4. Схема замещения катушки с магнитопроводом
Рисунок 6.5. Векторная диаграмма тушки с магнитопроводом. .
На рисунке 6.5 показаны вектор магнитной индукции и вектор напряженности:
И вектор напряженности:
Активная мощность, поступающая в катушку:
В некоторых случаях пользуются понятием реактивной мощности, равной U ф 1ф, причем удельную реактивную мощность, вар/кг, обозначают:-
Иногда приводятся кривые рСТ(Вт) и Q 0 (Вт), которые применяются при расчетах магнитных цепей электрических машин и аппаратов, работающих при частоте 50 Гц. Иногда при расчетах пользуются комплексным магнитным сопротивлением:
При появлении в магнитопроводе воздушного зазора l в составляющая r т увеличивается, поскольку на преодоление воздушного зазора магнитным потоком должна затрачиваться некоторая часть I ф, при этом соответственно возрастают b 0 и Q 0. Катушку с магнитопроводом удобно характеризовать некоторой усредненной нелинейной индуктивностью, зависящей от напряжения на ее выводах. При определении такой индуктивности по вольтамперной характеристике для действующих величин U и I различают две индуктивности: эквивалентную L Э = U / Iω и эквивалентную динамическую:
При определении по вольтамперной характеристике для первых гармоник различают соответственно:
где U 1 и I 1 - величины первых гармоник. Определение по показаниям приборов напряженности магнитного поля, магнитной индукции, потерь в магнитопроводе и построение векторной диаграммы катушки с магнитопроводом иллюстрированы примерами 6.1-6.3.
ПИК-ТРАНСФОРМАТОР
Пик-трансформатором называют трансформатор, вторичное напряжение которого и2 (t) имеет острую пикообразную форму. В отличие от силового трансформатора, у которого материал магнитопровода подбирается таким образом, чтобы обеспечить работу по возможности в линейном режиме, материал магнитопровода пик-трансформатора подбирается так, чтобы работа его протекала в резко выраженном нелинейном режиме. На рисунок 6.10, а представлена одна из наиболее простых схем пик-трансформатора. Магнитопровод 1 изготовляется из ферромагнитного материала с почти прямоугольной кривой намагничивания. Первичная обмотка с числом витков w 1 подключается к источнику тока синусоидальной формы i 1 = Im sin ω t, а во вторичной обмотке с числом витков наводится э. д. с. е2 пикообразной формы. Процесс получения е2 иллюстрируется рисунок 6.10, б. В левой части изображена характеристика Ф(i 1), повернутая для удобства построения на 90° против направления вращения часовой стрелки. В правой части рисунка даны характеристики i 1 (t), Ф(t) и е2 (t). Последовательность построения такова, на синусоидальной кривой i 1 (t) выбирается произвольная точка 1 и находится соответствующая ей точка 2 на кривой Ф(i 1) (масштабы i 1 (t) в обеих системах координат одинаковы); соответствующий точке 2 магнитный поток Ф определяется отрезком 0 '3, который переносится в систему координат Ф, таким образом, чтобы ордината Ф (т. е. точка 4) и ордината точки 1 соответствовали одному и тому же моменту времени. Таким образом определяются все точки кривой Ф(t).
Кривая е2 (t) строится по тангенсам углов касательных к кривой Ф (t). При Ф (t) = 0, где производная d Ф / dt максимальна, кривая е2 (t) имеет максимум. Максимум е2 (t) тем больше, чем круче Ф (t) при t = 0 и, следовательно, чем больше d Ф / di 1 при i 1 = 0.
Кривая е2 пик-трансформатора может быть получена и аналитическим методом при надлежащей аппроксимации кривой намагничивания В (Н), однако достаточно точное выражение е (t) получается сложным, так как оно должно содержать гармоники кратности выше третьей. ЯВЛЕНИЕ ФЕРРОРЕЗОНАНСА
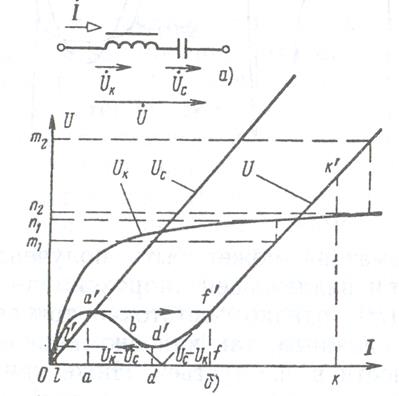
В отличие от линейной цепи, в которой изменение приложенного напряжения (или тока при питании от источника тока) не вызывает явления резонанса, в нелинейной цепи с ферромагнитным элементом возможны изменения знака угла сдвига фаз между основными гармониками напряжения и тока при изменении напряжения (или тока) источника питания. Резонанс в цепи, содержащей катушку с насыщенным магнитопроводом, соединенную последовательно или параллельно с конденсатором, называется феррорезонансом. При анализе явления феррорезонанса в целях упрощения пользуются эквивалентными синусоидами напряжения и тока в катушке. Обозначим действующие величины через UK и I к. Различают феррорезонанс напряжений и феррорезонанс токов. Феррорезонанс напряжений возникает при последовательном соединении катушки с магнитопроводом и конденсатора (рисунок 6.11, а). Так как связь между значениями Вт и Нт в магнитопроводе определяется динамической кривой намагничивания Вт = f (Нт), то и связь между UK и I к определяется вольт-амперной характеристикой, подобной кривой намагничивания. Это означает, что с увеличением тока I к в обмотке полное сопротивление катушки zK = UK / IK уменьшается. Сопротивление r к составляет небольшую долю полного сопротивления z к. Поэтому приближенно можно считать, что катушка имеет только индуктивное сопротивление хк ≈ zK.
Рисунок 6.11 Феррорезонанс напряжений.
При постепенном возрастании тока I от нуля (рисунок 6.11, б) напряжение UK будет изменяться по кривой, a Uc = 1/ωС по прямой, поскольку ω и С величины постоянные. Если питать цепь от источника напряжения, то приложенное напряжение определится как:
здесь предполагается, что На участке 0а/b, кривая | UK - Uc | = UK - Uc приблизительно совпадает с U Дальнейший ход кривой | UK - Uc | показан пунктиром; расхождение с кривой U обусловлено влиянием активной составляющей напряжения UK (активная составляющая UC практически равна нулю).
При токах, меньших 0 d, приложенное напряжение Участок a! d / кривой напряжения U является спадающим. Это означает, что при увеличении тока падение напряжения в цепи уменьшается и, следовательно, при неизменной э. д. с. источника энергии ток в цепи нарастает. Спадающий участок a ' d ' соответствует неустойчивому режиму работы цепи. Характеристика рисунок 6.11, б аналогична характеристике нелинейного элемента. Если цепь присоединена к источнику с весьма малым внутренним сопротивлением, то при постоянном возрастании э' Д. с. источника от нуля эту э. д. с. уравновешивает падение напряжения U, определяемое участком кривой 0 а' После этого уравновешивающее падение напряжения будет определяться частью кривой f ' k '. Участок a ' d ' f ' является нерабочим при возрастании напряжения. При постепенном увеличении приложенного к цепи напряжения (начиная с нуля) ток вначале плавно увеличивается до некоторого значения 0а, а затем он претерпевает скачок до нового значения 0 f (релейный эффект), после чего опять плавно увеличивается. Если уменьшать напряжение на выводах цепи (начиная со значения, большего ff /, то изменение уравновешивающего падения напряжения происходит сначала постепенно по участку f ' d ', а затем по участку l / 0. В этом случае участок d / a / l / является нерабочим. Ток постепенно уменьшается до значения 0 d и затем претерпевает скачок до значения 0 l. Неоднозначность характеристики U(I) рисунок 6.11,6 при заданных U препятствует экспериментальному снятию характеристики при питании цепи от источника э. д. с. Если же питать цепь от источника тока, то могут быть экспериментально сняты все точки характеристики, так как каждому заданному значению тока будет соответствовать только одно значение напряжения. На практике вместо источника тока для этой цели пользуются источником э. д. с. с достаточно большим добавочным сопротивлением, включенным последовательно. Схема рисунок 6.11, а может быть использована в качестве стабилизатора напряжения, на входе которого напряжение равно U, а на выходе UK. При изменении U от 0т1 до 0т2 напряжение UK изменяется в очень малых пределах от 0п1 до 0 n 2. Феррорезонанс токов возникает при параллельном соединении катушки с магнитопроводом и конденсатора (рисунок 6.12, а). Характер изменения токов в функции напряжения I (U), I к (U) и Ic (U) в цепи аналогичен характеру изменения напряжения в функции тока U (I), UK (I) и Uc (I) в цепи на рисункк 6.11, а. На рисунке 6.12, б изображены кривые токов при постепенном увеличении напряжения U от нуля. Если цепь рисунок 6.12, а питать от источника тока и постепенно изменять ток, то на выводах цепи будут иметь место скачкообразные изменения напряжения: от 0а до 0 f при увеличении тока и от 0 d до 0 l при убывании тока. Точка d ' соответствует резонансу токов.
Скачкообразные изменения тока при плавном изменении напряжения, а также скачкообразные изменения напряжения при плавном изменении тока называют релейным или триггерным эффектом. При питании цепи от источника напряжения общий ток в цепи определяется вольт-амперной характеристикой Oa / d ’ f / рисунок 6.12 ,б. Каждому заданному напряжению будет соответствовать только одно значение тока, и поэтому спадающий участок характеристики может быть снят экспериментально.
Рисунок 6.12. Феррорезонанс токов.
Как говорилось выше, феррорезонанс рассматривается на основе эквивалентных синусоид токов и напряжений, являющихся несинусоидальными функциями времени. При достижении резонанса амплитуда третьей гармоники общего тока цепи может в несколько раз превысить амплитуду первой гармоники. Следует заметить, что эффект, аналогичный феррорезонансу, может быть получен в цепи, составленной из линейной катушки индуктивности и нелинейного конденсатора, величина которого зависит от приложенного напряжения Явление феррорезонанса можно исследовать при помощи аппроксимации характеристики i (ψ) уравнением:
Если пренебречь активным сопротивлением цепи (рисунок 6.12, а) и принять напряжение на выводах цепи и = = Um sin ω t, дифференциальное уравнение цепи будет иметь вид:
где q - заряд конденсатора С В результате дифференцирования (6.5), подстановки (6.4) вместо i = dq / dt и замены a 1 / C = ω02, a 2 / C = h, ω Um = G получается известное в теории нелинейных систем уравнение Дуффинга:
Потокосцепление ψ при отсутствии потерь должно отличаться по фазе на ± π /2 от напряжения и. Решение уравнения (6.6) будем искать в форме
Поскольку здесь исследуется процесс по первой гармонике, слагаемое, содержащее cos 3ω t, отбрасывается:
Если в результате решения этого уравнения относительно А получаются три вещественных корня, в цепи возможны скачки амплитуды. При разделении (6.7) на две части:
значение А определится из условия у1 = у2. Для нахождения А удобно построить графики у1 (A) и у2 (A), показанные на рисункe 6.13.
Рисунок 6.13. Графическое решение кубического уравнения (6.7).
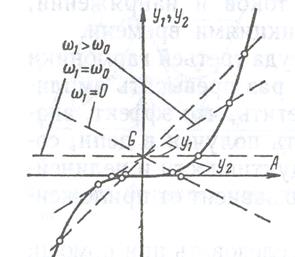
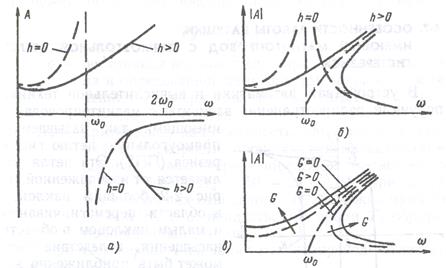
График у1 (A) представляет собой семейство прямых линий, наклон которых зависит от ω2 – ω02; у2(А) - кубическую параболу, а при h = 0 - ось абсцисс. На рисунке 6.13 наглядно видно, что при ω > ω0 возможны три значения А, два из которых отрицательны и одно положительно. Изменение знака А соответствует изменению фазы тока с +л/2 на - π /2 относительно фазы напряжения при прохождении резонансной частоты. На рисунок 6.14, а показаны зависимости А (ω), построенные по точкам пересечений у1 и у2 согласно рисунок 6.13. Пунктиром на рисунок 6.14, а показаны зависимости А (ω) при линейной связи между током и потокосцеплением, т. е. когда а2 = 0 и h = 0; при этом кривые приобретают вид, показанный на рисунке 6.11, б. На рисунке 6.14, б показаны зависимости абсолютного значения | А| от ω. На рисунке 6.14, в изображено семейство резонансных кривых нелинейного контура при разных G.
Рисунок 6.14. Зависимость амплитуды А от угловой частоты. а - с учетом знака А, при h = 0 контур линеен, при h > 0 контур нелинеен; б - для абсолютных значений А; в - с учетом влияния изменения.
Практически в цепи всегда имеются потери мощности. Поэтому ветви не уходят в бесконечность, а заканчиваются некоторым закруглением. Нижняя граница неустойчивого участка определится из выражения dA / dω = = ∞, что соответствует dω 2 / d А = 0. Решение (6.7) относительно ω2 дает:
откуда:
в результате подстановки значения G в (6.7) получается уравнение:
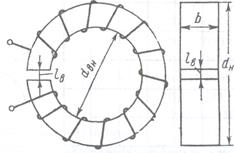
геометрического места точек скачкообразного увеличения амплитуды при изменении ω. Уравнение (6.7) позволяет также исследовать изменение | А| от G при фиксированном значении частоты ω. В этом случае прямая на рисунке 6.13 перемещается параллельно самой себе и зависимость G от | А\ получается подобной зависимости U от I, показанной на рисунок 6.11, б. Сценарий Практической работы № 4 по дисциплине «Теоретические основы электротехники» по направлению 13.03.02 Электроэнергетика и электротехника. Группа ЭЭ-16-Д(4-й семестр) Введение (10-15мин.) Цель работы: Отработать навыки р асчета цепей переменного тока с ферромагнитными элементами. Практическая часть Задание 1 Определить значения Вт и Нт в магнитопроводе катушки по результатам измерений в схеме рисунок 6.28, если приложенное напряжение U = 120 В, ток I = 0,3 А, частота f = 400 Гц. Магнитопровод изготовлен из листовой стали (рисунок 7) и имеет размеры dBH = 56 мм, dH = 83,5 мм, b = 20 мм, 1В = 0, коэффициент заполнения поперечного сечения сталью (коэффициент заполнения стали) k ст = 0,9; обмотка магнитопровода состоит из 200 витков. Для упрощения расчета активное сопротивление обмотки принимается равным нулю.
Рисунок 7 Тороидальный магнитопровод
Решение Магнитный поток согласно (6.3):
Активное сечение стали магнитопровода:
Амплитуда индукции магнитопровода:
Длина средней линии магнитопровода:
Амплитуда напряженности магнитного поля:
Задание 2. Для магнитопровода, рассмотренного в задании1, определить удельные потери в стали, если при частоте f 1 = 400 Гц, напряжении U = 120 В и токе 11 = 0,3 А мощность, измеряемая ваттметром (рисунок 8), равна р1 = 10 Вт.
Рисунок 8. Схема для приближенного определения параметров катушки с ферромагнитным магнитопроводом при переменном токе в обмотке. Произвести разделение потерь, если при уменьшении частоты до f 2 = 100 Гц, напряжения до U 2 = 30 В и тока до I 2 = 0,28 А показание ваттметра равно Р2 = 3 Вт. Сопротивление обмотки, измеренное при постоянном токе, равно r = 20 Ом. Потери в измерительных приборах принимаются равными нулю. Решение Масса магнитопровода
Так как э.д.с. Е = 4,44В m SCTf прямо пропорциональна частоте, то приближенно имеем:
Откуда B1m ≈ B2m. Проведем разделение потерь. Удельные потери в стали при частоте f 1 = 400 ГЦ:
Удельные потери в стали при частоте f 1 = 100 ГЦ:
В соответствии с выражениями (6.1) и (6ю2) можно записать:
где k Г и kB – коэффициенты пропорциональности: k Г = 2,98 10-2 Дж/кг и k В = 5,04 10-5 Дж/кг. При частоте f 1 = 400 Гц удельные потери на гистерезис:
и на вихревые токи:
При частоте f 2 = 100 Гц:
Задание 3 Построить векторную диаграмму катушки, рассмотренной в заданиях 1 и 2, при частоте f = 400 Гц, если индуктивность рассеяния катушки LS = 5 мГн. Решение Индуктивное сопротивление катушки это тоже, что и сопротивление рассеяния:
Сдвиг фаз между эквивалентной синусоидой тока и напряжения:
Комплексное сопротивление катушки:
Комплексное сопротивление ветвей намагничивания и потерь в стали:
Комплексная проводимость ветвей намагничивания и потерь в стали:
Проводимость ветви потерь в стали: g0 = 6,23 10-4; Проводимость ветви намагничивания: b 0 = 25,4 10-4; Ток потерь в стали:
Намагничивающий ток:
Угол потерь:
Электродвижущая сила: E = z0I = 382 x 0,3 =114,5B; Магнитный поток в магнитопроводе
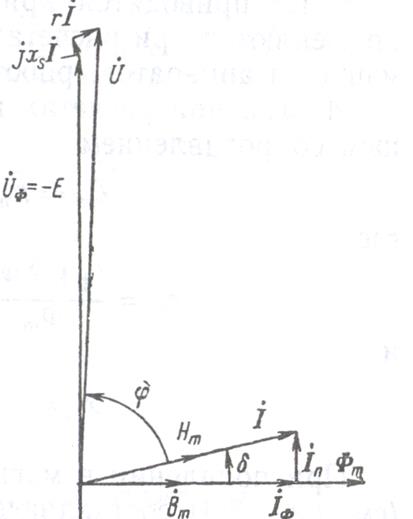
По значениям Ф m, Е, I ф, δ, I п, I, φ, r, xs, U построена векторная диаграмма на рисунке 9.
Рисунок 9. Векторная диаграмма катушки с магнитопроводом. Задание 4 На магнитопроводе, рассмотренном в примерах 1 - 3, кроме первой обмотки с числом витков wl = 200 дополнительно намотана вторая обмотка с числом витков w 2 = 100. Таким образом, получается трансформатор с коэффициентом трансформации:
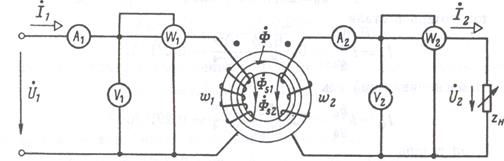
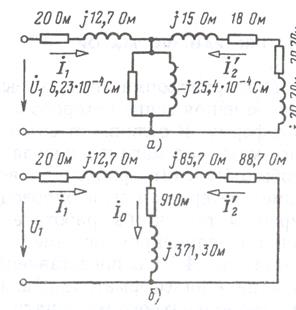
При замкнутой накоротко вторичной обмотке этого трансформатора, напряжении U 1 = 12 В и частоте f = 400 Гц ток I 1 = 0,249 А и мощность Р1 = 2,47 Вт. Определить показания приборов (рисунок 10) при напряжении U 1 = 120В, сопротивлении нагрузки ZH = 25∟45° Ом и построить векторную диаграмму.
Рисунок 10. Двухобмоточный трансформатор. Решение Угол между векторами первичного напряжения и тока:
Входное сопротивление (сопротивление короткого замыкания тран- cформатора):
Из задания 1 известно, что при y 0 = 120 В и разомкнутой вторичной обмотке индукции Вт ≈ 1,41 Тл. При U 1 = 12 В и замкнутой вторичной обмотке индукция уменьшится более чем в 10 раз, а напряженность поля уменьшится в несколько десятков раз вследствие нелинейной связи Вт ≈ f (Н т). Поэтому проводимость y 0 уменьшиться по сравнению с вычисленной в задании 3 в несколько десятков раз.
Сопротивление нагрузки, приведенное к первичной обмотке:
Рисунок 11. Задание 4
При напряжении U 1 = 120 В необходимо учитывать проводимость К0, которая может быть принята такой же, как в задании 3. Схема замещения трансформатора при нагрузке изображена на рисунке 11, а. На рисунке 11, б схема замещения преобразована для расчета, в Результате которого получается:
Остальные величины, необходимые для построения векторной диаграммы. получаются в результате следующих вычислений:
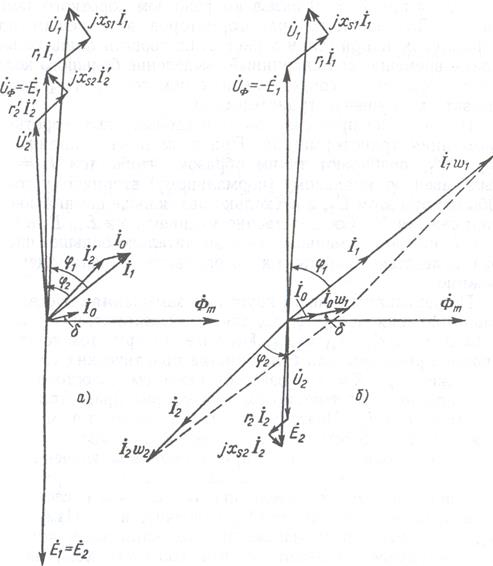
Начальная фаза вектора I 0 равна углу потерь δ = 13°45', вычисленному в задании 3. Векторные диаграммы на рисунке 12 построены по полученным в данном примере значениям напряжений и токов.
Рисунок 12. Векторные диаграммы трансформатора: для встречного (а) и согласного (б) направлений токов.
Задание 5 Напряженность магнитного поля в магнитопроводе пик-трансформатора изменяется по закону Н = 725 sin 2512 t А/м. Определить э. д. с. в обмотке из w = 1000 витков, насаженной намагнитопровод, если поперечное сечение стали магнитопровода S = 0,9 см2, а связь между индукцией В и напряженностью Н может быть представлена в виде В = 3 10-3 Н – 2 10-9 Н3, Тл. Решение Магнитный поток в магнитопроводе:
Контрольные вопросы ЗАДАЧИ И ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ 4-1. Потери на гистерезис в ферромагнитном материале рп — 0 1 Вт/кг при частоте ft = 100 Гц. Определить потери на гистерезис рг2 при частоте = 400 Гц, если индукция изменяется по синусоидальному закону и амплитуда ее сохраняется неизменной. Ответ: 4 Вт/кг. 4-2. Потери на вихревые токи в ферромагнитном материале рв1 = = 0,5 Вт/кг при частоте Д = 100 Гц. Определить потери на вихревые токи рв2 при частоте 400 Гц, если индукция изменяется по синусоидальному закону и амплитуда ее сохраняется неизменной. Ответ: 8 Вт/кг. 4-3. В результате испытаний образца стали из листов толщиной Дх = 0,1 мм и Д2 = 0,35 мм были определены потери на гистерезис рг и потери на вихревые токи рв. для листов толщиной Дг = 0,1 мм рт = 1,1 Вт/кг; рв = 0,1 Вт/кг; для листов толщиной Д2 = 0,35 мм рт = 0,5 Вт/кг; ра = 0,3 Вт/кг. Испытания проводились при частоте /=50 Гц. Определить потери рст в этих сортах стали при частотах 50, 150 и 400 Гц, если индукция во всех случаях синусоидальна и ее амплитуда неизменна. Ответ: Для 1,2; 4,23; 15,2 Вт/кг; для Д2 0,8; 4,24; 23,2 Вт/кг. 4-4. При частоте /, = 100 Гц потери в стали рсг1 = 2 Вт/кг, при частоте /2 = 200 Гц потери в стали рсх2 = 7 Вт/кг. Определить потери в стали рстз при частоте /3 = 400 Гц, если индукция изменяется по синусоидальному закону и амплитуда ее сохраняется неизменной. Ответ: 26 Вт/кг. 4-5. Магнитопровод, изображенный на рис. 2-4, изготовлен из стальной ленты и имеет размеры dBH = 45 мм, da = 60 мм, 6=15 мм, 1В = 0. Коэффициент заполнения поперечного сечения магнитопрово- дов сталью £ст = 0,85. Магнитное поле в магнитопроводе характеризуется индукцией, изменяющейся по синусоидальному закону с частотой f = 1000 Гц и амплитудой Вт = 0,8 Тл. Материал магнитопровода характеризуется динамической кривой намагничивания рис. 4-1. На магнитопровод намотана обмотка, состоящая из w — 1000 витков. Определить наводимую э. д. с. и ток в обмотке. Ответ: 340 В, 0,175 А. 4-6. Потери в материале магнитопровода из задачи 4-5 рг = = 20 Вт/кг и рв = 40 Вт/кг. Определить угол потерь. Ответ: 8°30'. 4-7. Последовательно с обмоткой на магнитопроводе из задачи 4-5 соединен конденсатор С =0,1 мкФ. Определить напряжение на выводах цепи, если сопротивление обмотки г — 100 Ом и индуктивность рассеяния Ls = 0. Ответ: 91В. 4-8. Определить э. д. с. и ток в обмотке задачи 4-5 при частоте /= 50 Гц и амплитуде индукции Вт = 0,8 Тл. О т в е т: 17 В; 0,035 А. 4-9. Определить угол потерь б для задачи 4-5 при /= 50 Гц и Вт = 0,8 Тл, если учесть, что потери в материале магнитопровода при частоте 1000 Гц приведены в задаче 4-6. Ответ: 13°. 4-10. Определить напряжение на выводах обмотки задачи 4-5 при / = 50 Гц, Вт = 0,8 Тл, г = 100 Ом и Ls = 0. Ответ: 17,3 В. 4-11. В цепь катушки включены приборы, как показано на рис. 4-2. Напряжение на выводах цепи U = 120 В. При наличии стального магнитопровода ток в обмотке / = 0,69 А и мощность Р = 32,2 Вт. При отсутствии магнитопровода ток в обмотке I = 2,23 А и мощность Р = 100 Вт. Определить параметры схемы замещения катушки с маг- нитопроводом в соответствии с рис. 4-4 и построить векторную диаграмму, если сопротивление рассеяния xs = 23 Ом. Ответ: г = 20 Ом, g 0 — 0,00227 См, Ь0 = 0,0065 См. 12. Как влияет изменение частоты на форму динамической кривой намагничивания? Порядок выполнения работы 1. Внимательно изучить общие теоретические сведения (20 минут). 2. Прорешать на доске под руководством преподавателя 4 задания. (60 минут). 3. Самостоятельно, на основе алгоритма решения по п. 2 выполнить задания в соответствии с вариантом в таблице 1. (70 минут). Вариант выбирается в соответствии с номером в журнале. 4. Письменно ответить на теоретические вопросы. 20(минут). 5. Оформить решения в соответствии с примером и сдать преподавателю. (10 минут).
Таблица 1
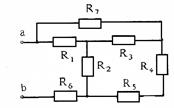
Пример оформления самостоятельного задания Студент: Ф.И.О., гр.ЭЭ-14-З1, Вариант 1 Определить эквивалентное сопротивление R Э (рисунки 7,8,9) относительно указанных зажимов, если сопротивления равны 10 Ом.
Дано: Исходная схема R7 = 0; R 1, R 2, R 3, R 4, R 5, R 6 = 10 O м. RЭab =? Решение: 1. Промежуточные схемы пошагово. 2. Расчет по действиям с комментариями. Ответ: RЭ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 259; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.92.25 (0.017 с.) |

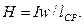
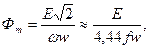 (6.3)
(6.3)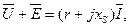
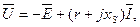
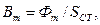
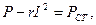
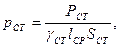
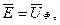
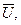 затрачиваемого на преодоление э. д. с. Ё.
затрачиваемого на преодоление э. д. с. Ё.
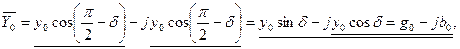

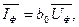 и тока потерь в стали
и тока потерь в стали 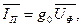 . Если принять, что Фт совпадает с действительной осью комплексной плоскости, то ток
. Если принять, что Фт совпадает с действительной осью комплексной плоскости, то ток 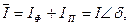 .
.
 m
m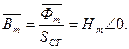
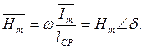
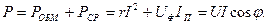
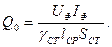
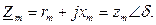
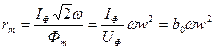
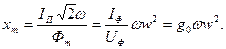
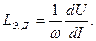
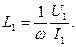
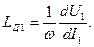

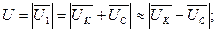
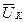 опережает ток I на угол, близкий к 90°.
опережает ток I на угол, близкий к 90°.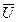 опережает ток
опережает ток 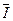 , а при токах, больших 0 d, отстает. Току 0 d соответствует минимальное напряжение dd ', равное активной составляющей напряжения. При этом эквивалентные синусоиды напряжения и тока совпадают по фазе, а UK немного превышает Uc (за счет активной составляющей). Точка d ' соответствует резонансу напряжения.
, а при токах, больших 0 d, отстает. Току 0 d соответствует минимальное напряжение dd ', равное активной составляющей напряжения. При этом эквивалентные синусоиды напряжения и тока совпадают по фазе, а UK немного превышает Uc (за счет активной составляющей). Точка d ' соответствует резонансу напряжения.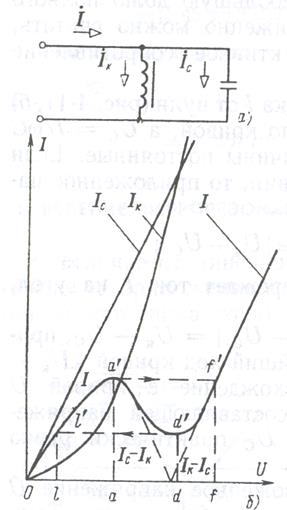
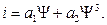 (6.4)
(6.4)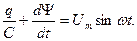 (6.5)
(6.5)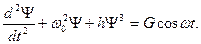 (6.6)
(6.6)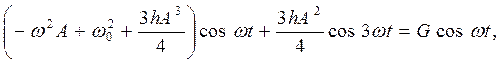 ψ = = A cosωt. В результате подстановки этой функции в (6.6) и учета соотношения cos 3 ω t = 1/4(3 cos ω t + cos 3ω t) получается:
ψ = = A cosωt. В результате подстановки этой функции в (6.6) и учета соотношения cos 3 ω t = 1/4(3 cos ω t + cos 3ω t) получается: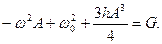 (6.7)
(6.7)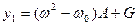 и
и 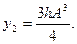
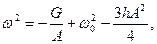
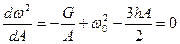 и
и 
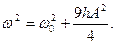
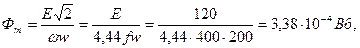
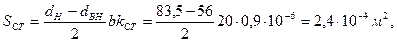
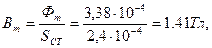
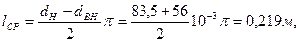
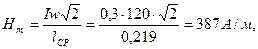
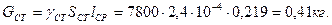

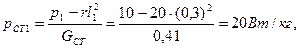
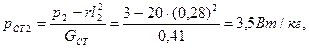
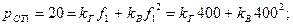
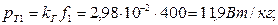
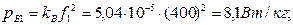
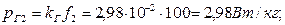
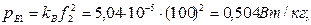
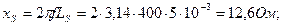
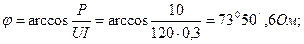
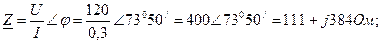
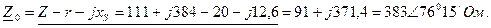
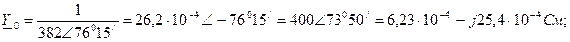
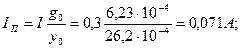
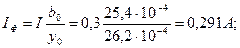
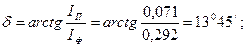
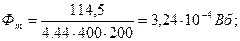
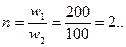
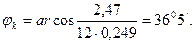
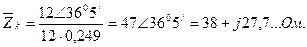
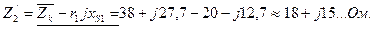
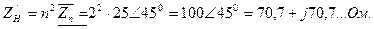




 Задание 1.
Задание 1.


