Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Катушки индуктивности с магнитопроводомСодержание книги
Поиск на нашем сайте
При подключении к обмотке катушки с числом витков W (рисунок 1) переменного напряжения u (t) по обмотке будет протекать переменный ток i (t) и создавать переменный магнитный ноток
где Образованный магнитный поток, пересекая витки обмотки, наводит в ней ЭДС самоиндукции, которая совместно с падением напряжения на активном сопротивлении обмотки R будет уравновешивать приложенное напряжение:
где
Рисунок 1. Катушка индуктивности с магнитопроводом
Из (1.13) вытекает, что
Рисунок 2. Кривая намагничивания магнитопровода (а), форма тока в катушке индуктивности (б) и эквивалентная синусоида тока (в)
Для вычисления параметров, связывающих несинусоицяльные величины, целесообразно перейти от реальной несипусоидальнои функции к эквивалентной по площади синусоидальной (рисунок 2, а), что позволит применить метод комплексных амплитуд и выражение (1.14) в комплексной форме будет иметь вид:
где
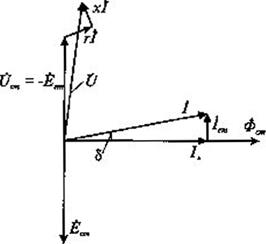
Рисунок 3 - Векторная диаграмма катушки индуктивности с магнитопроводом
Этому уравнению соответствует векторная диаграмма (рисунок 3). где δ - угол магнитного запаздывания; I СТ - активная составляющая тока катушки, обусловленная активными потерями в стали; I М - намагничивающая составляющая тока катушки, совпадающая по фазе с магнитным потоком. Векторная диаграмма представляет собой изображение на комплексной плоскости уравнения (1.13) электрического равновесия катушки; схемы замещения катушки имеют вид. показанный на рисунке 4. Наличие магнитопровода к катушке значительно увеличивает магнитную проницаемость магнитной цени и индуктивность катушки, которая прямо пропорциональна величине магнитной проницаемости (1.10).
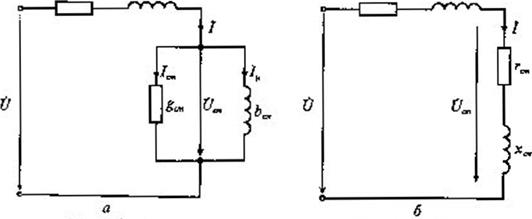
Рисунок 4 - Схема замещения катушки индуктивности
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.61.131 (0.008 с.) |

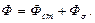 (1.13)
(1.13)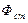 - основная часть магнитного потока, замыкающаяся по магнитопроводу; Фа - часть магнитного потока, замыкающаяся ко неферромагнитной среде (воздуху), называемая потоком рассеяния.
- основная часть магнитного потока, замыкающаяся по магнитопроводу; Фа - часть магнитного потока, замыкающаяся ко неферромагнитной среде (воздуху), называемая потоком рассеяния.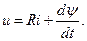 (1.14)
(1.14)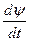 - ЭДС самоиндукции; ᴪ = Li = W Ф - потокосцепление, L - индуктивность катушки; i - мгновенный ток катушки.
- ЭДС самоиндукции; ᴪ = Li = W Ф - потокосцепление, L - индуктивность катушки; i - мгновенный ток катушки.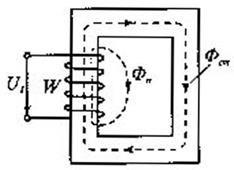
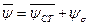 , но потокосцепление
, но потокосцепление  (1.14)
(1.14)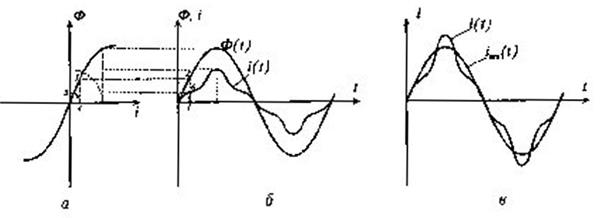
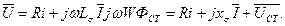 (1.15)
(1.15)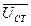 - ЭДС самоиндукции, возникающая в обмотке катушки под действием магнитного потока
- ЭДС самоиндукции, возникающая в обмотке катушки под действием магнитного потока 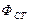 , замыкающегося по магнитопроводу:
, замыкающегося по магнитопроводу: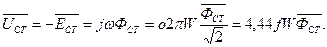 (1.16)
(1.16)