Основные свойства ферромагнитных материалов при переменных магнитных полях
При изменении магнитного поля в ферромагнитном материале часть энергии магнитного поля преобразуется в теплоту. Мощность, соответствующая этой части энергии, называется потерями в сталии обозначается Рст; в расчетах обычно пользуются удельными потерями в стали Рст, измеряемыми в ваттах на килограмм.
Потери в стали состоят из потерь на гистерезис (потерь на перемагничивание) и динамических потерь. Удельные потери на гистерезис, обозначаемые РГ, вызываются необратимыми процессами в стали при перемене ориентации областей самопроизвольного намагничивания; они пропорциональны частоте. Для вычисления удельных потерь на гистерезис применяется приближенная формула
 (6.1) (6.1)
где  и и 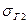 - коэффициенты, зависящие от сорта материала, f - частота; - коэффициенты, зависящие от сорта материала, f - частота;
Вт - амплитуда магнитной индукции.
Динамические потери вызываются вихревыми токами, индуктированными в массе магнитного материала, и отчасти магнитной вязкостью, которая особенно заметно проявляется на крутых участках петли гистерезиса (вблизи Н = Нс) при малых изменениях поля. В большом числе практических случаев динамические потери можно отождествлять с потерями на вихревые токи.
Удельные потери на вихревые токи могут быть представлены следующей формулой:
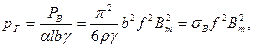 (6.2) (6.2)
где b - толщина листа;
γ - плотность стали;
σ - коэффициент, зависящий от сорта стали и толщины листа.
Из формулы (6.2) видно, что рв пропорционально квадрату частоты и квадрату толщины листа. Следовательно, одним из способов уменьшения рв является уменьшение толщины листа. Однако листы нельзя изготовлять чрезмерно тонкими. В частности, уменьшению толщины листов препятствует то обстоятельство, что при этом увеличиваются удельные потери на гистерезис рг. Для различных частот существуют различные оптимальные толщины листов. Например, при частоте 400 Гц применяют листы толщиной 0,1—0,35 мм, а при частоте 50 Гц листы толщиной 0,35 и 0,5 мм.
При синусоидальном магнитном потоке вихревые токи можно считать отстающими от магнитного потока на четверть периода.
Магнитодвижущая сила, создаваемая вихревыми токами, должна компенсироваться частью м. д. с. обмотки. Поэтому ток в обмотке должен иметь составляющую, находящуюся в противофазе с вихревыми токами, т. е. опережащую магнитный поток на четверть периода.
При частотах порядка тысяч герц и выше сказывается поверхностный эффект, в результате которого магнитная индукция неодинаково распределяется по сечению магнитопровода (она больше на периферии и меньше в центре сечения).
Из-за поверхностного эффекта и увеличения потерь в стали применение магнитопроводов, собранных из стальных листов, при высоких частотах нецелесообразно. При высоких частотах применяют магнитопроводы из ферритов обладающих большим удельным электрическим сопротивлением.
Различие в зависимостях рг и рв от частоты [выражения (6.1) и (6.2)] позволяет определить, какая именно часть потерь затрачивается на гистерезис и какая на вихревые токи, или, как говорят, разделить потери.
Для разделения потерь достаточно знать суммарные потери в магнитопроводе для двух частот при неизменной Вт.
Потери в стали обусловливают несовпадение по фазе индукции В и напряженности поля Н, характеризуемое углом потерь δ. Если В и Н - несинусоидальные функции времени, то δ является сдвигом фаз между соответствующими эквивалентными синусоидами.
Если представить индукцию и напряженность поля в виде комплексных амплитуд:
 и и 
то магнитная проницаемость может быть представлена в комплексной форме:

где μ0 = 4л 10-7 Гн/м - магнитная постоянная;
μ r 1 и μ r 2 - действительная и мнимая части относительной комплексной магнитной проницаемости (квазиупругая и поглощающая проницаемости)
Понятие о комплексной магнитной проницаемости было введено В К. Аркадьевым в 1913 г
Завимимость между амплитудными значениями индукции Вт и напряженности Нт при определенной частоте в предположении, что эти величины синусоидальны, называется динамической кривой намагничивания
При одном и том же материале магнитопровода с увеличением частоты динамические кривые намагничивания располагаются ниже и становятся более пологими, как показано на рисунке 6.1.
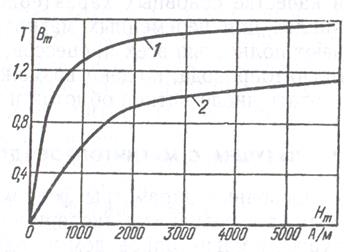
Рисунок 6.1. Динамические кривые намагничивания:
1 - при частоте 50 Гц; 2 - при частоте 1000 Гц
Эти кривые приближённо характеризуют зависимость В = f (Н) и не отображают ее неоднозначность. Неоднозначная зависимость В = f (Н) характеризуется динамической петлей гистерезиса. Ширина петли возрастает
Кривые получены в результате испытаний для конкретного сорта стали. Для других сортов характер кривых может существенно отличаться с увеличением частоты магнитного поля. Расширение петли гистерезиса вызывается увеличением составляющей, компенсирующей вихревые токи (динамические потери). При этом увеличиваются одновременно не только гистерезис, но и вихревые токи, что в ряде случаев весьма удобно.
Листовые ферромагнитные материалы с целью улучшения магнитных свойств подвергают особой обработке, в результате которой материалы приобретают магнитную анизотропию, т. е. зависимость магнитной проницаемости и. от направления напряженности магнитного поля. Магнитопроводы при этом конструируют таким образом, чтобы направление магнитного поля соответствовало наибольшим значениям μ r. Такая конструкция дает возможность производить расчет магнитной цепи так же, как и в случае изотропных материалов. Магнитные свойства некоторых типов материалов резко ухудшаются при появлении в них механических напряжений. Магнитопроводы из таких материалов приходится помещать в специальные кожухи из диэлектрика, на который наматывается обмотка, для предотвращения механического сжатия магнитопровода витками обмотки.
Свойством изменения в зависимости от механических напряжений обладают по существу все ферромагнитные материалы. На этом, например, основано определение механических напряжений в стальных конструкциях посредством измерения переменных магнитных полей, создаваемых в отдельных небольших участках этих конструкций. Однако для большого.количества электрических машин, трансформаторов, реле и т. п. механические напряжения, обычно появляющиеся в магнитопроводах, практически не оказывают влияния на их работу.
Здесь имеются в виду кольцевые магнитопроводы устройств автоматики.
При расчете любого устройства, содержащего магнитную цепь с переменным магнитным полем, необходимо учитывать явления, обусловленные главным образом гистерезисом и вихревыми токами. Для учета этих явлений используются такие величины, как потери в стали, угол потерь, комплексная магнитная проницаемость и т. д., а также динамическая кривая намагничивания и динамическая петля гистерезиса.
Указанные величины и параметры можно принимать в качестве основных характеристик ферромагнитных материалов при переменных магнитных полях. Они не описывают полностью всех процессов, происходящих в материале магнитопровода, но дают возможность достаточно точно рассчитать число витков обмоток и размеры магнитопровода.
КАТУШКА С МАГНИТОПРОВОДОМ
Основные параметры ферромагнитного материала определяют в результате экспериментального исследования катушки с магнитопроводом из однородного ферромагнитного материала, одинакового поперечного сечения, без воздушного зазора. Для такого исследования предпочтительна тороидальная форма магнитопровода, так как при этом обеспечиваются наиболее точные измерения.
С помощью приборов, показанных на схеме рисунок 6.2, можно определить основные параметры характеристики ферромагнитного материала.
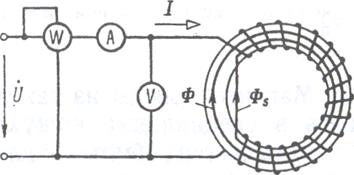
Рисунок 6.2. Схема для приближенного определения параметров катушки с ферромагнитным магнитопроводом при переменном токе в обмотке.
При исследовании обычно известны число витков обмотки до, активное сопротивление обмотки г, сечение магнитопровода SCT, длина средней линии напряженности поля l ср и частота f. По показаниям электроизмерительных приборов определяют ток I, напряжение U на выводах обмотки и потребляемую мощность Р (при определении Р из показания ваттметра необходимо вычесть мощности потерь в амперметре и вольтметре).
Действующая напряженность Н магнитного поля определяется по формуле:
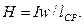
При синусоидальном напряжении амплитуда магнитного потока, замыкающегося по магнитопроводу катушки:
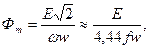 (6.3) (6.3)
где Е - действующая э. д. с., наводимая в обмотке вышеуказанным магнитным потоком.
Кроме магнитного потока Ф, замыкающегося по магнитопроводу катушки, имеется еще магнитный поток рассеяния Ф S, замыкающийся через воздух и показанный на рисунке 6.2 условно (поток рассеяния может быть сцеплен лишь с частью витков обмотки). Так как магнитное сопротивление воздуха значительно больше магнитного сопротивления магнитопровода, поток Ф S можно считать совпадающим по фазе с током и прямо пропорциональным ему Это дает возможность учитывать э. д. с., наводимую потоком рассеяния, с помощью сопротивления рассеяния xS '.
Так как положительные направления тока и наведенной потоком Ф S э. д. с. совпадают, то сумма приложенного напряжения и наведенной э. д. с. равна падению напряжения в активном сопротивлении и сопротивлении рассеяния:
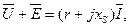
Откуда:
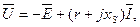
В большинстве случаев Е мало отличается от U. Амплитуда магнитной индукции:
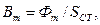
Разность между мощностью, потребляемой катушкой, и мощностью, затрачиваемой на нагрев обмотки, равна потерям мощности в стали магнитопровода:
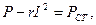
Удельные потери в стали:
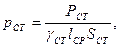
где γ CT - плотность материала магнитопровода.
Для катушки с магнитопроводом характерными являются два режима работы:
1.напряжение на выводах обмотки синусоидально, а ток в обмотке несинусоидален;
2.ток в обмотке синусоидален, а напряжение на выводах несинусоидально.
В первом случае при r ≈ 0 можно принять магнитный поток синусоидальным и построить кривую тока i (t). Порядок построения кривой i (t) показан на рисунке 6.3. На кривой магнитного потока Ф(t) произвольно выбирается точка посредством горизонтальной линии 1-2, пересекающей кривую Ф (t), и вертикальной линии 2- 3 определяется значение тока i, равное абсциссе 0-3 и соответствующее значению (ординате) потока в точке 1; это значение тока откладывается в виде ординаты 0-4 и переносится в координатную систему i (t) посредством проведения горизонталь ной линии 6.5 до пересечения с вертикальной прямой 1- 5. При выборе исходных точек на нисходящей части кривой abc значение тока i определяется также по нисходящей ветви abc петли Ф (t).
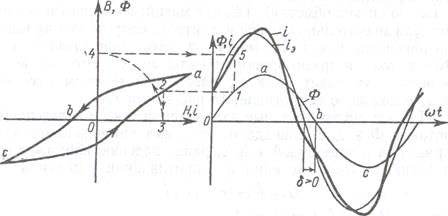
Рисунок 6.3. Графическое определение тока в катушке при синусоидальном магнитном потоке.
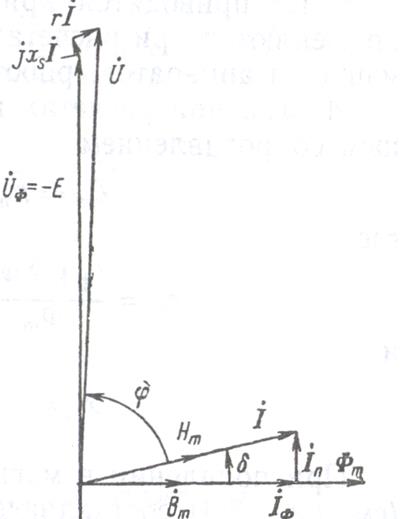
Изображенная на рисунке 6.3 кривая i (t) симметрична относительно оси абсцисс, что означает отсутствие четных гармоник. Эквивалентная синусоида тока i сдвинута по фазе относительно магнитного потока Ф на угол δ.
При синусоидальном приложенном напряжении э. д. с., наводимая в обмотке, несинусоидальна вследствие появления высших гармонических составляющих в токе. Однако искажение э. д. с. обычно незначительно и, представляя ее в виде эквивалентной синусоиды, можно принять - 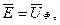
где U ф - составляющая приложенного напряжения 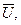 затрачиваемого на преодоление э. д. с. Ё. затрачиваемого на преодоление э. д. с. Ё.
Отношение:

- комплексная проводимость ветвей намагничивания и потерь в стали;
у0 - полная проводимость ветвей намагничивания и потерь в стали:
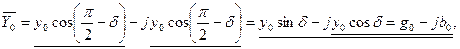
где g 0 - проводимость ветви потерь в стали; b - проводимость ветви намагничивания.
Иногда в расчетах применяется комплексное сопротивление ветвей намагничивания и потерь в стали:

Ток в обмотке представляется в виде двух составляющих: намагничивающего тока 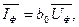 и тока потерь в стали и тока потерь в стали 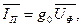 . Если принять, что Фт совпадает с действительной осью комплексной плоскости, то ток . Если принять, что Фт совпадает с действительной осью комплексной плоскости, то ток 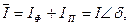 . .
В соответствии со сказанным изображаются схемы замещения (рисунок 6.4) и векторная диаграмма (рисунок 6.5) катушки с магнитопро- водом.
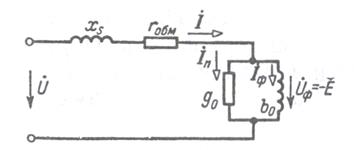
Рисунок 6.4. Схема замещения катушки с магнитопроводом
 m m
Рисунок 6.5. Векторная диаграмма тушки с магнитопроводом. .
На рисунке 6.5 показаны вектор магнитной индукции и вектор напряженности:
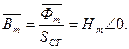
И вектор напряженности:
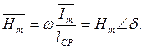
Активная мощность, поступающая в катушку:
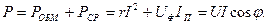
В некоторых случаях пользуются понятием реактивной мощности, равной U ф 1ф, причем удельную реактивную мощность, вар/кг, обозначают:-
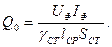
Иногда приводятся кривые рСТ(Вт) и Q 0 (Вт), которые применяются при расчетах магнитных цепей электрических машин и аппаратов, работающих при частоте 50 Гц.
Иногда при расчетах пользуются комплексным магнитным сопротивлением:
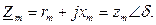
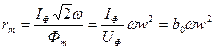
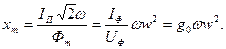
При появлении в магнитопроводе воздушного зазора l в составляющая r т увеличивается, поскольку на преодоление воздушного зазора магнитным потоком должна затрачиваться некоторая часть I ф, при этом соответственно возрастают b 0 и Q 0.
Катушку с магнитопроводом удобно характеризовать некоторой усредненной нелинейной индуктивностью, зависящей от напряжения на ее выводах. При определении такой индуктивности по вольтамперной характеристике для действующих величин U и I различают две индуктивности: эквивалентную L Э = U / Iω и эквивалентную динамическую:
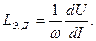
При определении по вольтамперной характеристике для первых гармоник различают соответственно:
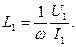
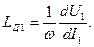
где U 1 и I 1 - величины первых гармоник.
Определение по показаниям приборов напряженности магнитного поля, магнитной индукции, потерь в магнитопроводе и построение векторной диаграммы катушки с магнитопроводом иллюстрированы примерами 6.1-6.3.
|