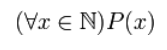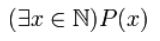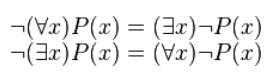Правила построения таблицы истинности.

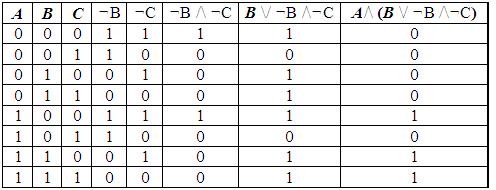
Таблица истинности - таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.

Логическое выражение - составные высказывания в виде формулы.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».

Правила построения таблицы истинности:

1. подсчитать количество переменных n в логическом выражении;

2. определить число строк в таблице по формуле m=2ⁿ, где n - количество переменных;

3. подсчитать количество логических операций в формуле;

4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5. определить количество столбцов: число переменных + число операций;

6. выписать наборы входных переменных;

7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

       3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

Пример 1. Для формулы A/\ (B \/ B /\C) постройте таблицу истинности.

Количество логических переменных 3, следовательно, количество строк - 2³ = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов - 3 + 5 = 8.

Пример. Для формулы A/\ (B \/ B /\C) постройте таблицу истинности.

 

 

Исчисление предикатов. Кванторные правила и ограничение переменных.

Предикат - утверждение, которое содержит переменные, принимающие значение 1 или 0 (истинно или ложно) в зависимости от значений переменных.
Например, выражение x=x5 является предикатом, т.к. оно является истинным при x=0 или x=1 и ложным при всех остальных значениях x.

Множество, на котором предикат принимает только истинные значения, называется множеством истинности предиката Ip.

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение: P(x1,…,xn)=1

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение: P(x1,…,x0)=0

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Т.к. предикаты могут принимать только два значения (истинно/ложно или 0/1), то к ним можно применять все операции алгебры логики: отрицание, конъюнкция, дизъюнкция и т.д.

Примеры предикатов

Пусть предикат R(x,y): «» «x=y» обозначает отношение равенства, где x и y принадлежат множеству целых чисел. В этом случае предикат R будет принимать истинное значение для всех равных x и y.

Другой пример предиката -- РАБОТАЕТ(x,y,z) для отношения «x работает в городе y в компании z».

Еще один пример предиката -- НРАВИТСЯ(x,y) для «x нравится y» для x и y, которые принадлежат M -- множеству всех людей.

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

Операции над предикатами Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Конъюнкция двух предикатов A(x) и B(x) -- предикат, который принимает истинное значение при тех и только тех значениях x из T, при которых каждый из предикатов принимает истинное значение, а ложное значение -- во всех остальных случаях. Множество истинности T предиката -- пересечение множеств истинности предикатов A(x) и B(x). Например: предикат A(x): «x -- чётное число», предикат B(x): «x делится на 5». Таким образом, предикатом будет выражение «x -- чётное число и делится на 5» или «x делится на 10».

Дизъюнкция двух предикатов A(x) и B(x) -- предикат, который принимает ложное значение при тех и только тех значениях x из T, при которых каждый из предикатов принимает ложное значение и принимает истинное значение во всех остальных случаях. Множество истинности предиката -- объединение областей истинности предикатов A(x) и B(x).

Отрицание предиката A(x) -- предикат, который принимает истинное значение при всех значениях x из T, при которых предикат A(x) принимает ложное значение и наоборот. Множество истинности предиката A(x) -- дополнение T′ к множеству T в множестве x.
Импликация предикатов A(x) и B(x) -- предикат, который является ложным при тех и только тех значениях x из T, при которых A(x) -- истинно, а B(x) -- ложно, и принимает истинное значение во всех остальных случаях. Читается: «Если A(x), то B(x)».

Пример 2 Пусть A(x): «Натуральное число x делится на 3»; B(x): «Натуральное число x делится на 4». Составим предикат: «Если натуральное число x делится на 3, то оно делится и на 4».

Множество истинности предиката -- объединение множества истинности предиката B(x) и дополнения к множеству истинности предиката A(x). Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.

Кванторы -- логические операторы, применение которых к предикатам превращает их в ложные или истинные высказывания.

Квантор -- логические операции, которые ограничивают область истинности предиката и создают высказывание.

Чаще всего используют кванторы:

квантор всеобщности (обозначается символом ∀x) -- выражение «для всех x» («для любого x»);

квантор существования (обозначается символом ∃x) -- выражение «существует x такое, что...»;

квантор единственности и существования (обозначается ∃!x) -- выражение «существует точно одно такое x, что...».

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов Пусть -- предикат «x кратно 7». С помощью квантора всеобщности можно записать следующие ложные высказывания: любое натуральное число делится на 7; каждое натуральное число делится на 7; все натуральные числа делятся на 7; который будет иметь вид:

для записи истинных высказываний используем квантор существования: существуют натуральные числа, которые делятся на 7; найдётся натуральное число, которое делится на 7; хотя бы одно натуральное число делится на 7. Запись будет иметь вид:

Пусть на множестве x простых чисел задан предикат: «Простое число является нечетным». Поставив перед предикатом слово «любое», получим ложное высказывание: «Любое простое число является нечетным» (например, 2 является простым четным числом). Поставим перед предикатом слово «существует» и получим истинное высказывание: «Существует простое число, которое является нечетным» (например, x=3). Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

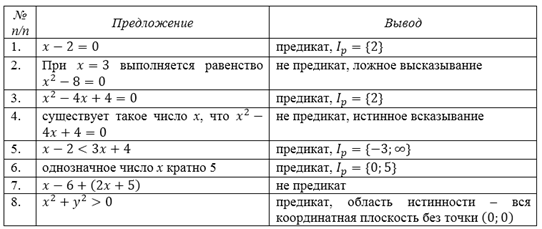
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них: