
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические операции над бинарными отношениями.Содержание книги
Поиск на нашем сайте
Над бинарными отношениями можно производить некоторые операции, точно так же, как и над множествами. Не ограничивая общности, будем считать, что следующие операции выполняются на множестве Пересечение. Пересечением двух бинарных отношений ( Например, пересечением отношения «не меньше» и «не равно» является отношение «больше». Объединение. Объединением двух бинарных отношений ( Например, объединением отношения «больше» и отношения «равно» является отношение «больше, либо равно». Включение. Обозначается
Принципы классификации По своей логической структуре классификация представляет собой операцию, основанную на делении понятий. Однако классификация отличается от деления понятий в двух отношениях: 1) если деление может производиться по любому возможному основанию, то классификация осуществляется по признаку, имеющему существенное значение для распределения исследуемых объектов. Большей частью она используется для систематизации накопленных знаний в разных областях науки, и поэтому носит более устойчивый характер, чем простое деление понятий; 2) при классификации распределение объектов производится по существенным признакам, в то время как деление можно провести по отличительным признакам. Очевидно, что такое отличие не является абсолютным хотя бы потому, что предпосылкой даже научной классификации служит первоначальное разграничение объектов и понятий по их отличительным, а не существенным признакам. Таким образом, классификацией называется распределение объектов по тому или иному существенному свойству, в результате чего каждый из них попадает в точно указанный класс, подмножество или группу. Понятие классификации применимо, следовательно, не только к объемам понятий, но и к тем реальным предметам, которые подпадают под эти понятия. О классификации говорят также и тогда, когда расчленяют сложный предмет на его составные части. Такую классификацию называют мерологической.
12 Правила определения. Ошибки, связанные с их нарушением. Определение – логическая операция, раскрывающее содержания имени или устанавливающее значения термина. Правила определений: Определение должно быть соразмерным, т. е. объём определяющего имени должен быть равен объему определяемого имения. В результате нарушения данного правила возникают следующие логические ошибки: «широкое определение», когда объём определяющего имени больше определяемого, и «узкое определение», когда объём определяющего имени меньше определяемого («Солнце – это небесное тело» (широкое определение); «Птица – это животное, имеющее крылья и умеющее летать» (узкое определение)). Определение не должно содержать круга, т.е. когда определяемое и определяющее имя выражаются одно через другое. В результате нарушения данного правила возникает логическая ошибка, которая называется «тавтология» («Клеветник – это человек, который занимается клеветой»). Определение должно быть четким и ясным. Это правило означает, что смысл и объем имён, входящих в определяющее имя должен быть ясным и определенным. Определения должны быть свободными от двусмысленности; не допускается подмена их метафорами, сравнениями и т. д. («Математика – это гимнастика для ума»).
|
||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.135.24 (0.01 с.) |

 .
. и
и  ) является отношение, которое определяется пересечением соответствующих подмножеств. Очевидно, что отношение
) является отношение, которое определяется пересечением соответствующих подмножеств. Очевидно, что отношение  выполнимо только в том случае, когда некоторые
выполнимо только в том случае, когда некоторые  и
и  связаны как первым, так и вторым отношением (
связаны как первым, так и вторым отношением ( и
и 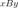 ).
).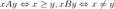 , тогда
, тогда 
 и
и  ) является отношение, которое определяется объединением соответствующих подмножеств. Отношение
) является отношение, которое определяется объединением соответствующих подмножеств. Отношение  выполнимо только в том случае, когда некоторые
выполнимо только в том случае, когда некоторые  связаны хотя бы одним из двух отношений хотя бы одно из отношений (
связаны хотя бы одним из двух отношений хотя бы одно из отношений ( или
или  ).
). . Первое отношение включено во второе, если все те пары, для которых выполняется первое отношение, являются подмножеством пар, для которых выполняется второе отношение. Если
. Первое отношение включено во второе, если все те пары, для которых выполняется первое отношение, являются подмножеством пар, для которых выполняется второе отношение. Если  , то
, то  . Если
. Если  , то, когда любые два элемента из множества, на котором выполняется отношение
, то, когда любые два элемента из множества, на котором выполняется отношение  , связаны этим отношением, они связаны отношением
, связаны этим отношением, они связаны отношением 


