Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды понятий (по объему, по содержанию, по универсуму).Содержание книги
Поиск на нашем сайте
Этапы становления логики Формальная логика в своем развитии прошла два основных этапа. Первый этап - это связь с работами Аристотеля, в которых дано систематическое изложение логики. Основным содержанием логики Аристотеля является теория дедукции, также содержаться элементы математической логики. Аристотель сформулировал основные законы мышления: тождества, противоречия и исключенного третьего, описал важнейшие логические операции, разработал теорию понятия и суждения, обстоятельно исследовал дедуктивное умозаключение. Учение о силлогизме составило основу одного из направлений современной математической логики - логике предикатов. Дополнением к этому учению была логика античных стоиков (Зенон, Хрисипп и других). Логика стоиков -основа другого направления математической логики - логики высказываний. Следующими, кто развил учение Аристотеля, следует назвать Галена; Порфирия, который разработал схему отображающую отношения между понятиями; Боэция, сочинения которого были логическими пособиями. Логика развивалась и в средние века, однако схоластика исказила учение Аристотеля, приспособив его для обоснования религиозной догматики. Значительны успехи логической науки в Новое время. Важнейшим этапом в ее развитии явилась теория индукции, разработанная Ф. Беконом. Он подверг критике дедуктивную логику, которая не может служить методом научных открытий. Методом должна быть индукция. Разработка индуктивного метода - огромная заслуга Бекона. Методы дедукции и индукции не исключают друг друга, а дополняют. Дж.С.Милль систематизировал методы научной индукции. Дедуктивная логика Аристотеля и индуктивная логика Бекона Милля составили основу общеобразовательной дисциплины и составляют основу логического образования в настоящее время. Второй этап – это появление математической логики. Философ Г. В. Лейбниц считается основоположником. Он пытался построить универсальный язык, с помощью которого споры между людьми можно было разрешить посредством вычисления. Математическая логика изучает логические связи и отношения, лежащие в основе дедуктивного вывода. Для выявления структуры вывода строят различные математические исчисления. 2 Предмет и основные понятия логики Для выяснения предмета логики можно использовать несколько методов, каждый из которых дает определенный результат. Термин «логика» восходит к древнегреческому слову «логос», означавшему слово, мысль, понятие, рассуждение и закон. Древнегреческие философы считали, что в речах человека есть некая сила. Она побуждает, сказав «А», сказать и «Б». В основе этого принуждения лежит человеческий разум, который отыскивает в природе необходимое и отбрасывает случайное. Этимология слова «логика» показывает, что это наука, имеющая отношение к человеческому мышлению, обосновывает рассуждения с помощью оснований, которые впоследствии стали называться логическими законами. Логика – наука о законах и формах человеческого мышления, рассматриваемого как средство познания окружающей действительности. Сложно выделить одно определенное значение, которое бы в целом могло охарактеризовать такую древнюю науку. К примеру, предметом логики считается исследование законов выведения правильных определенных суждений и утверждений из определенных истинных обстоятельств. Так характеризовал эту древнею науку Фридрих Людвиг Готлоб Фреге. Понятие и предмет логики изучал и Шуман Андрей Николаевич – известный логик современности. Он считал, что это наука о размышлениях, которая исследует различные способы мышления и моделирует их. Кроме того, объект и предмет логики — это, конечно же, речь, ведь логика осуществляется только при помощи разговора или дискуссии, и абсолютно неважно, вслух или «про себя». Если говорить простым языком, то логика — это мыслительный процесс поиска истины, ведь на основе ее принципов формируется процесс поиска научного познания. Основные понятия логики. Абстрагирование – логический приём, в ходе которого происходит мысленное выделение одних признаков предмета и отвлечение от других, не существенных признаков Анализ [греч. análysis – разложение] – логический приём, в ходе которого происходит мысленное расчленение предметов на их составные части и выделение в них признаков Аргумент [лат. argumentum – логический довод, основание доказательства] – суждение (или совокупность взаимосвязанных суждений), посредством которого обосновывается истинность какого-либо другого суждения (или теории) Вероятностные умозаключения - то же самое, что и правдоподобные умозаключения Восприятие – целостный образ предмета, возникающий в результате его непосредственного воздействия на органы чувств Вывод логический – рассуждение, в ходе которого из каких-либо исходных суждений – посылок с помощью логических правил получают заключение – новое суждение Гипотеза [греч. hypóthesis – основание, предположение] – 1) форма развития знаний, представляющая собою обоснованное предположение, выдвигаемое с целью выяснения свойств и причин исследуемых явлений]; 2) вероятностное предположение о причине каких-либо явлений, достоверность которого при современном состоянии производства и науки не может быть проверена и доказана, но которое объясняет данные явления, без него необъяснимые; приём познавательной деятельности Дедуктивное умозаключение [лат. deductio – выведение] – форма абстрактного мышления, в которой мысль развивается от знания большей степени общности к знанию меньшей степени общности, а заключение, вытекающее из посылок, с логической необходимостью носит достоверный характер Деление по видоизменению признака - деление, как правило, более чем на две части, каждой из которых присущ признак, взятый за основание, но в особом его проявлении Деление понятия – логическая операция, раскрывающая объём понятия Делимое понятие - понятие, объём которого подвергается делению Довод – составная часть всякого доказательства, под которой понимается мысль, истинность которой проверена и доказана и которая поэтому может быть приведена в обоснование истинности или ложности высказанного положения Догма [греч. dogma – мнение, учение] – утверждение, принимаемое в качестве истинного на веру, без обоснования или сопоставления с фактами; основание учения, сформулированного как систематизированная вера Доказательство - логическое рассуждение, в процессе которого обосновывается истинность или ложность какой-либо мысли с помощью других положений, проверенных наукой и конкретной практикой Единичное понятие – понятие, в котором мыслится один предмет Единичное суждение – суждение, включающее утверждение или отрицание об одном предмете Заблуждение – несоответствие субъективных представлений (мнений, верований и т.п.) человека объективному положению вещей Зависимые суждения – суждения, которые имеют одинаковые составляющие и могут различаться логическими связками, включая отрицание Заключение (вывод) умозаключения – суждение, логически выведенное из предшествующих посылок и содержащее новое знание Закон мышления - внутренняя, существенная, устойчивая, необходимая, повторяющаяся связь между элементами мысли и самими мыслями Закон достаточного основания – всякая истинная мысль должна быть обоснована другими мыслями, истинность которых доказана Закон противоречия - не могут быть одновременно истинными две противоположные мысли об одном и том же предмете, взятом в одно и то же время и в одном и том же отношении Закон тождества - каждая мысль, которая приводится в данном умозаключении, при повторении должна иметь одно и то же определённое, устойчивое содержание Индуктивное определение [лат. inductio – наведение] – определение, позволяющее из некоторых исходных объектов теории с помощью некоторых операций строить новые объекты теории Индуктивное умозаключение (индукция) [лат. inductio – наведение] – 1) умозаключение, в котором на основании принадлежности признака отдельным предметам или частям некоторого класса делают вывод о его принадлежности классу в целом ]; 2) форма абстрактного мышления, в которой мысль развивается от знания меньшей степени общности к знанию большей степени общности, а заключение, вытекающее из посылок, носит преимущественно вероятностный характер Истина – знание, которое адекватно отражает в сознании человека явления и процессы объективного мира Концепция [лат. conceptio – понимание, система] - целостная система абстрактных объектов, отражающая наиболее существенные закономерности исследуемого предмета. В логике и других науках различные концепции служат основой для построения теорий Логика [греч. logos – слово, понятие, рассуждение, разум] - наука о законах и операциях правильного мышления Мышление – высшая форма отражения объективной реальности, состоящая в целенаправленном и обобщённом познании субъектом существенных связей и отношений предметов и явлений, в творческом созидании новых идей, в прогнозировании событий и действий Общая гипотеза – обоснованное предположение о закономерных связях в природе и обществе и об эмпирических регулярностях Общее понятие – понятие, в котором мыслится множество предметов Парадигма [греч. parádeigma – пример, образец] – 1) совокупность теоретических и методологических положений, принятых научным сообществом на известном этапе развития науки и используемых в качестве образца, модели, стандарта для научного исследования, интерпретации, оценки и систематизации научных данных, для осмысления гипотез и решения задач, возникающих в процессе научного познания ]; 2) исходная концептуальная схема, модель постановки проблем и их решения, методов исследования, господствующих в течение определённого исторического периода в научном сообществе Простое суждение – 1) суждение, выражающее связь двух понятий ]; 2) суждение, представляющее собой одно утверждение или отрицание; состоит из одного субъекта и одного предиката ]. Синтез [греч. sýnthesis – соединение] – логический приём, в ходе которого происходит мысленное соединение в единое целое частей предмета или его признаков, полученных в процессе анализа Суждение – форма мышления, в которой что-либо утверждается или отрицается о существовании предметов, связях между предметом и его свойствами или об отношениях между предметами Тезис [греч. thesis – положение, утверждение] – один из элементов доказательства, положение, истинность которого обосновывается в доказательстве Тождественные (равнозначные) понятия – совместимые понятия, объёмы которых полностью совпадают Умозаключение – форма мышления, посредством которой из одного или нескольких суждений, связанных между собой, с логической необходимостью выводится новое суждение Факт – знание, основанное на чувственных восприятиях и выраженное единичным суждением Элемент множества [лат. elementum – стихия, первоначальное вещество] – объект, предмет, входящий в какое-либо множество, которому присущи признаки, характерные для данного множества. Правила терминов. 1. В силлогизме должно быть только три термина (в результате нарушения данного правила возникает логическая ошибка, которая называется «учетверение терминов»). 2. Средний термин должен быть распределён по крайней мере в одной из посылок. 3. Термин не может быть распределён в заключении, если он не распределён в посылке. Правила посылок. 1.Из двух отрицательных посылок нельзя сделать заключения; 2. Из двух частных посылок нельзя сделать заключения; 3. Если одна из посылок отрицательная, то и заключение должно быть отрицательным; 4. Если одна из посылок частная, то и заключение должно быть частным. Закон тождества альный число модус А Если высказывание истинно, то оно истинно. Закон непротиворечия (А&А) Два противоречащих друг другу высказывания не могут быть одновременно истинными. Закон исключенного третьего А Из двух противоречащих друг другу высказываний по крайней мере одно истинно. Закон двойного отрицания А Двойное отрицание высказывания равнозначно его утверждению. Законы Де Моргана (А&В) Отрицание конъюнкции равнозначно дизъюнкции двух отрицаний. (А Отрицание дизъюнкции равнозначно конъюнкции двух отрицаний. Закон контрапозиции (A Если из одного высказывания вытекает второе, то из отрицания второго вытекает отрицание первого. Примеры предикатов Пусть предикат R(x,y): «» «x=y» обозначает отношение равенства, где x и y принадлежат множеству целых чисел. В этом случае предикат R будет принимать истинное значение для всех равных x и y. Другой пример предиката -- РАБОТАЕТ(x,y,z) для отношения «x работает в городе y в компании z». Еще один пример предиката -- НРАВИТСЯ(x,y) для «x нравится y» для x и y, которые принадлежат M -- множеству всех людей. Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения. Операции над предикатами Рассмотрим применение операций алгебры логики к предикатам. Логические операции: Конъюнкция двух предикатов A(x) и B(x) -- предикат, который принимает истинное значение при тех и только тех значениях x из T, при которых каждый из предикатов принимает истинное значение, а ложное значение -- во всех остальных случаях. Множество истинности T предиката -- пересечение множеств истинности предикатов A(x) и B(x). Например: предикат A(x): «x -- чётное число», предикат B(x): «x делится на 5». Таким образом, предикатом будет выражение «x -- чётное число и делится на 5» или «x делится на 10». Дизъюнкция двух предикатов A(x) и B(x) -- предикат, который принимает ложное значение при тех и только тех значениях x из T, при которых каждый из предикатов принимает ложное значение и принимает истинное значение во всех остальных случаях. Множество истинности предиката -- объединение областей истинности предикатов A(x) и B(x). Отрицание предиката A(x) -- предикат, который принимает истинное значение при всех значениях x из T, при которых предикат A(x) принимает ложное значение и наоборот. Множество истинности предиката A(x) -- дополнение T′ к множеству T в множестве x. Пример 2 Пусть A(x): «Натуральное число x делится на 3»; B(x): «Натуральное число x делится на 4». Составим предикат: «Если натуральное число x делится на 3, то оно делится и на 4». Множество истинности предиката -- объединение множества истинности предиката B(x) и дополнения к множеству истинности предиката A(x). Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д. Кванторы -- логические операторы, применение которых к предикатам превращает их в ложные или истинные высказывания. Квантор -- логические операции, которые ограничивают область истинности предиката и создают высказывание. Чаще всего используют кванторы: квантор всеобщности (обозначается символом ∀x) -- выражение «для всех x» («для любого x»); квантор существования (обозначается символом ∃x) -- выражение «существует x такое, что...»; квантор единственности и существования (обозначается ∃!x) -- выражение «существует точно одно такое x, что...». В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле. Примеры применения кванторов Пусть -- предикат «x кратно 7». С помощью квантора всеобщности можно записать следующие ложные высказывания: любое натуральное число делится на 7; каждое натуральное число делится на 7; все натуральные числа делятся на 7; который будет иметь вид:
для записи истинных высказываний используем квантор существования: существуют натуральные числа, которые делятся на 7; найдётся натуральное число, которое делится на 7; хотя бы одно натуральное число делится на 7. Запись будет иметь вид:
Пусть на множестве x простых чисел задан предикат: «Простое число является нечетным». Поставив перед предикатом слово «любое», получим ложное высказывание: «Любое простое число является нечетным» (например, 2 является простым четным числом). Поставим перед предикатом слово «существует» и получим истинное высказывание: «Существует простое число, которое является нечетным» (например, x=3). Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор. Операции над кванторами Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:
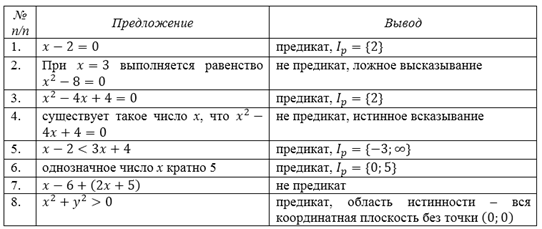
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:
Отношение совместимости К совместимым относятся такие сравнимые суждения, которые одновременно могут быть истинными. В сложных суждениях, как и в простых, различают три вида совместимости: эквивалентность, частичная совместимость и подчинение. 1. Эквивалентные — это суждения, которые принимают одни и те же значения, т. е. одновременно являются либо истинными, либо ложными. Отношение эквивалентности позволяет выражать одни сложные суждения через другие — конъюнкцию через дизъюнкцию или импликацию и наоборот. Приведем четыре известные эквивалентности, которые являются законами логики. 1) Выражение конъюнкции через дизъюнкцию: ?(A? B)??A??B 2) Выражение дизъюнкции через конъюнкцию: ?(A? B)??A??B Эти две эквивалентности называются законами де Моргана. 3) Выражение импликации через конъюнкцию: ?(A? B)? (A??B) 4) Выражение импликации через дизъюнкцию: A? B??A? B 2. Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными. Отношение частичной совместимости для сложных суждений показано в таблице 9, где А и В — схемы сложных суждений;? — знак частичной совместимости. 1-я строка таблицы говорит об одновременной истинности А и В; 2-я и 3-я — несовпадение значений; 4-я строка зачеркнута, поскольку исключается одновременная ложность А и В. 3. Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего подчиненное всегда будет истинным. Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующею все виды рассуждений. Отношение несовместимости Понятие отношения. Содержание, объем и местность отношений. Понятие - это форма мышления, в которой отражаются существенные признаки одноэлементного класса или класса однородных предметов. Все понятия находятся в самых различных логических отношениях друг с другом. Отношения устанавливаются между ними с одинаковым родом посредством сопоставления либо их объемов, либо содержаний. Отношения между понятиями можно классифицировать на основе важнейших логических характеристик: содержания и объема. 1) Отношение между понятиями по их содержанию: - сравнимые – понятия, имеющие в своем содержании общие существенные признаки; - несравнимые – понятия, не имеющие сколько-нибудь существенных общих признаков. 2) Отношение между понятиями по их объему: - совместимые – понятия, объемы которых полностью или хотя бы частично совпадают. - несовместимые – объемы не совпадают полностью. Отношения между понятиями принято иллюстрировать при помощи кругов Эйлера (круговых схем).
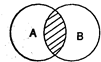
Например, объемы понятий А - «сын» и В - «внук» совпадают (каждый сын есть чей-то внук и каждый внук - чей-то сын), но содержания их различны. В отношении пересечения находятся совместимые понятия, у которых объемы частично совпадают. Частично совпадает и содержание данных понятий.
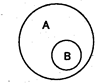
В отношении подчинения находятся совместимые понятия, объем одного из которых полностью входит в объем другого, составляя его часть.
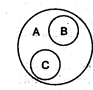
Объем первого понятия шире объема второго понятия: кроме кражи личного имущества граждан в него входит также кража государственного, кооперативного имущества. Из двух понятий, находящихся в отношении подчинения, понятие с большим объемом (подчиняющее) является родовым, или родом по отношению к понятию с меньшим объемом (подчиненному), а последнее по отношению к первому называется видовым, или видом. Родовидовые отношения лежат в основе логических операций ограничения и обобщения понятий, деления объема понятий и некоторых видов определения. При иллюстрации отношений между несовместимыми понятиями возникает потребность во введении более широкого по объему понятия, которое включало бы объемы несовместимых понятий. В отношении соподчинения находятся два или более непересекающихся понятий, принадлежащих общему родовому понятию. Соподчиненные понятия В и С - это виды одного рода А, у них общий родовой признак, но видовые признаки различны. Например, В - «должностное преступление» и С - «хозяйственное преступление», где А - «преступление».
В отношении противоположности находятся понятия, которые являются видами одного и того же рода, и при этом одно из них содержит какие-то признаки, а другое эти признаки отрицает и заменяет противоположными признаками. Например, А - «тяжкое телесное повреждение» и В - «легкое телесное повреждение», где родовое понятие - «телесное повреждение». Объемы противоположных понятий составляют лишь часть объема общего для них родового понятия.
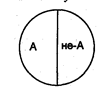
В отношении противоречия находятся такие два понятия, которые являются видами одного и того же рода, и при этом одно понятие указывает на некоторые признаки, а другое эти признаки отрицает, исключает, не заменяя их никакими другими признаками. Например, А - «виновный» и не-А - «невиновный», где родовое понятие - «человек». Объемы двух противоречащих понятий составляют весь объем рода, видами которого они являются. Отношения различаются «местностью». Отношения, представляющие предметно-истинные функции от одного аргумента, называют одноместными, а те, которым соответствует функция двух аргументов, - двухместными. Правила посылок 1-е правило: из двух отрицательных посылок заключение сделать нельзя. Хотя бы одна из посылок должна быть утвердительным суждением. Например: Студенты нашего ВУЗа не изучают высшую математику Сотрудники НИИ не являются студентами Из данных посылок нельзя получить необходимого заключения, так как оба крайних термина исключаются из среднего. Поэтому средний термин не может установить определенного отношения между крайними терминами. В заключении меньший термин может полностью исключаться из него. В соответствии с этим возможны три случая: “Все сотрудники НИИ изучают высшую математику”; “Некоторые сотрудники НИИ изучают высшую математику”; “Ни один сотрудник НИИ не изучает высшую математику”. 2-е правило: если одна из посылок – отрицательное суждение, то и заключение должно быть отрицательным. Поэтому в силлогизме с одной отрицательной посылкой средний термин исключается из объема крайнего термина, поэтому объем крайнего термина, который входит в объем среднего, исключается из объема другого крайнего термина. Например: Все гейзеры - горячие источники Этот источник не является горячим Этот источник не является гейзером В положительной посылке говорится о включении среднего термина в крайний, а в отрицательной - об исключении другого крайнего термина из среднего. Поэтому в заключении крайние термины несовместимы и исключают друг друга. Из утвердительных посылок нельзя получить отрицательное заключение, т. к. в утвердительных посылках заключается знание о полном или частичном совпадении объёмов терминов и отсутствует знание о несравнимости их объёмов. 3-е правило: из двух частных посылок заключение не следует. Хотя бы одна из посылок должна быть общим суждением. Например: Некоторые животные яйцекладущие Некоторые организмы – животные Если обе посылки - частные, то между крайними терминами возможны разные отношения. Если при этом обе посылки - частноутвердительные суждения, то заключения из них невозможно, т. к. средний термин не распределен ни в большей посылке (как субъект частного суждения), ни в меньшей (как предикат утвердительного суждения). Однако это противоречит ранее сформулированному правилу среднего термина. Если обе посылки – частноотрицательные суждения, то вывод сделать нельзя согласно 1-му правилу посылок. Если же одна из посылок - частноутвердительное суждение, а другая - частноотрицательное, то и в этом случае не выполняются правило крайних терминов силлогизма. 4-е правило: если одна из посылок – частное суждение, то и заключение должно быть частным. Например: Все слоны имеют хоботные Некоторые животные - слоны Некоторые животные хоботные Если одна из посылок - частная, а заключение - общее, то это означает нарушение правил терминов. Таким образом, в любом виде простого категорического силлогизма должны выполняться вышеперечисленные правила. Нарушение любого из них делает вывод неправильным, а заключение - ложным.
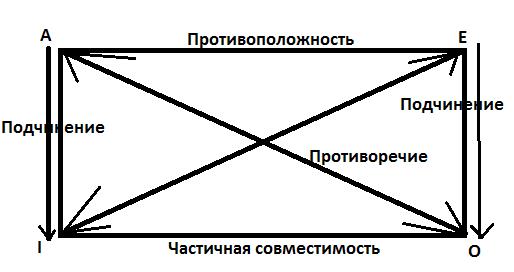
Логический квадрат Это изобретение средневековых логиков. Это способ систематизации для для лучшего восприятия. Отношения по логическому квадрату – это отношения между простыми суждениями по их истинности. Зная значение одного суждения можно узнать значение другого.
Правила логического квадрата: 1) Противоположные суждения не могут быть вместе истинными, но могут быть вместе ложными. Следствия: 1) А (и) -> Е (л). 2) Е (и) -> А (л). Но, если А (л) -> Е (и/л). И если Е (л) -> А (и/л). – неопределенные. 2) Частично совместимые суждения не могут быть вместе ложными, но могут быть вместе истинными. Следствия: 1) I(л) -> О (и). 2) О (л) ->I(и). Но: I(и) -> О (и/л). И если, О (и) ->I(и/л). Его значение будет неопределенным. 3) Противоречащие суждения не могут быть вместе ни истинными, ни ложными. Противоречащие суждения по диагонали не могут иметь одинаковых значений. Следствия: А (и) <-> О (л), Е (и) <-> I(л) И А (л) <-> О (и), Е (л) <->I(и). 4) Подчинение: Если общее суждение истинно, то необходимо истинно соответствующее ему частное суждение, но не наоборот. Из истинности частного суждения, значение общего суждения не определяется. Следствия: А (и) -> I(и), Е (и) -> О (и), ноI(и) -> А (и/л), О (и) -> Е (и/л) 5) Подчинение: Если частное суждение ложно, то необходимо ложным будет соответствующее ему общее суждение, но не наоборот. Из лжи общего, нельзя сделать вывод о лжи частного суждения. Следствия: I(л) -> А (л), О (л) -> Е (л), НО А (л) ->I(и/л), Е (л) -> О (и/л).
Этапы становления логики Формальная логика в своем развитии прошла два основных этапа. Первый этап - это связь с работами Аристотеля, в которых дано систематическое изложение логики. Основным содержанием логики Аристотеля является теория дедукции, также содержаться элементы математической логики. Аристотель сформулировал основные законы мышления: тождества, противоречия и исключенного третьего, описал важнейшие логические операции, разработал теорию понятия и суждения, обстоятельно исследовал дедуктивное умозаключение. Учение о силлогизме составило основу одного из направлений современной математической логики - логике предикатов. Дополнением к этому учению была логика античных стоиков (Зенон, Хрисипп и других). Логика стоиков -основа другого направления математической логики - логики высказываний. Следующими, кто развил учение Аристотеля, следует назвать Галена; Порфирия, который разработал схему отображающую отношения между понятиями; Боэция, сочинения которого были логическими пособиями. Логика развивалась и в средние века, однако схоластика исказила учение Аристотеля, приспособив его для обоснования религиозной догматики. Значительны успехи логической науки в Новое время. Важнейшим этапом в ее развитии явилась теория индукции, разработанная Ф. Беконом. Он подверг критике дедуктивную логику, которая не может служить методом научных открытий. Методом должна быть индукция. Разработка индуктивного метода - огромная заслуга Бекона. Методы дедукции и индукции не исключают друг друга, а дополняют. Дж.С.Милль систематизировал методы научной индукции. Дедуктивная логика Аристотеля и индуктивная логика Бекона Милля составили основу общеобразовательной дисциплины и составляют основу логического образования в настоящее время. Второй этап – это появление математической логики. Философ Г. В. Лейбниц считается основоположником. Он пытался построить универсальный язык, с помощью которого споры между людьми можно было разрешить посредством вычисления. Математическая логика изучает логические связи и отношения, лежащие в основе дедуктивного вывода. Для выявления структуры вывода строят различные математические исчисления. 2 Предмет и основные понятия логики Для выяснения предмета логики можно использовать несколько методов, каждый из которых дает определенный результат. Термин «логика» восходит к древнегреческому слову «логос», означавшему слово, мысль, понятие, рассуждение и закон. Древнегреческие философы считали, что в речах человека есть некая сила. Она побуждает, сказав «А», сказать и «Б». В основе этого принуждения лежит человеческий разум, который отыскивает в природе необходимое и отбрасывает случайное. Этимология слова «логика» показывает, что это наука, имеющая отношение к человеческому мышлению, обосновывает рассуждения с помощью оснований, которые впоследствии стали называться логическими законами. Логика – наука о законах и формах человеческого мышления, рассматриваемого как средство познания окружающей действительности. Сложно выделить одно определенное значение, которое бы в целом могло охарактеризовать такую древнюю науку. К примеру, предметом логики считается исследование законов выведения правильных определенных суждений и утверждений из определенных истинных обстоятельств. Так характеризовал эту древнею науку Фридрих Людвиг Готлоб Фреге. Понятие и предмет логики изучал и Шуман Андрей Николаевич – известный логик современности. Он считал, что это наука о размышлениях, которая исследует различные способы мышления и моделирует их. Кроме того, объект и предмет логики — это, конечно же, речь, ведь логика осуществляется только при помощи разговора или дискуссии, и абсолютно неважно, вслух или «про себя». Если говорить простым языком, то логика — это мыслительный процесс поиска истины, ведь на основе ее принципов формируется процесс поиска научного познания. Основные понятия логики. Абстрагирование – логический приём, в ходе которого происходит мысленное выделение одних признаков предмета и отвлечение от других, не существенных признаков Анализ [греч. análysis – разложение] – логический приём, в ходе которого происходит мысленное расчленение предметов на их составные части и выделение в них признаков Аргумент [лат. argumentum – логический довод, основание доказательства] – суждение (или совокупность взаимосвязанных суждений), посредством которого обосновывается истинность какого-либо другого суждения (или теории) Вероятностные умозаключения - то же самое, что и правдоподобные умозаключения Восприятие – целостный образ предмета, возникающий в результате его непосредственного воздействия на органы чувств Вывод логический – рассуждение, в ходе которого из каких-либо исходных суждений – посылок с помощью логических правил получают заключение – новое суждение Гипотеза [греч. hypóthesis – основание, предположение] – 1) форма развития знаний, представляющая собою обоснованное предположение, выдвигаемое с целью выяснения свойств и причин исследуемых явлений]; 2) вероятностное предположение о причине каких-либо явлений, достоверность которого при современном состоянии производства и науки не может быть проверена и доказана, но которое объясняет данные явления, без него необъяснимые; приём познавательной деятельности Дедуктивное умозаключение [лат. deductio – выведение] – форма абстрактного мышления, в которой мысль развивается от знания большей степени общности к знанию меньшей степени общности, а заключение, вытекающее из посылок, с логической необходимостью носит достоверный характер Деление по видоизменению признака - деление, как правило, более чем на две части, каждой из которых присущ признак, взятый за основание, но в особом его проявлении Деление понятия – логическая операция, раскрывающая объём понятия Делимое понятие - понятие, объём которого подвергается делению Довод – составная часть всякого доказательства, под которой понимается мысль, истинность которой проверена и доказана и которая поэтому может быть приведена в обоснование истинности или ложности высказанного положения Догма [греч. dogma – мнение, учение] – утверждение, принимаемое в качестве истинного на веру, без обоснования или сопоставления с фактами; основание учения, сформулированного как с<
|
||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 90; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.122.140 (0.019 с.) |

 A
A А
А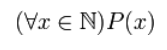
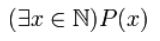
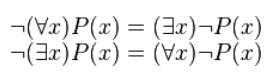
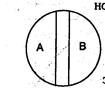
 В отношениях равнозначности находятся совместимые понятия, объемы которых полностью совпадают. В таких понятиях мыслится один и тот же предмет или класс однородных предметов. Однако содержание этих понятий различно, так как каждое из них отражает только определенную сторону (существенный признак) данного предмета или класса однородных предметов.
В отношениях равнозначности находятся совместимые понятия, объемы которых полностью совпадают. В таких понятиях мыслится один и тот же предмет или класс однородных предметов. Однако содержание этих понятий различно, так как каждое из них отражает только определенную сторону (существенный признак) данного предмета или класса однородных предметов.