Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выявление отношений для принятия управленческих решенийСодержание книги
Поиск на нашем сайте
Выявление отношений на множестве альтернатив осуществляет ЛПР или привлекаемый им специалист (эксперт) на основе своего представления о полезности сравниваемых вариантов. Будем полагать, что для любого ЛПР на множестве альтернатив A существует система предпочтений в том смысле, что ЛПР умеет сравнивать между собой любые два элемента a i и aj из предъявленного множества. Это означает, что при сравнении двух указанных произвольных элементов для ЛПР имеет место всегда один из трех альтернативных вариантов суждения: а) элемент ai предпочтительнее элемента aj; б) оба предъявленных элемента одинаково предпочтительны; в) элемент aj предпочтительнее элемента ai. Случаи «а» и «в» означают, что при многократном предъявлении этих элементов ЛПР его выбор среди них будет всегда однозначен – только первый в случае «а», и только второй – в случае «в». При многократном предъявлении элементов в случае «б» ЛПР всегда отвечает, что выбор одного из этих элементов ему безразличен. Других вариантов суждения, подобных высказываниям: «я не могу ничего сказать» или «я не знаю», не должно быть. При выполнении этого условия предпочтения ЛПР обладают свойством полноты. Кроме того, идеальные предпочтения ЛПР на предъявленном множестве элементов должны обладать свойством транзитивности. Это означает, что если ЛПР последовательно сравнивает три каких-то элемента попарно, т. е. первый и второй, а затем второй и третий и при этом, например, считает, что первый предпочтительнее второго, а второй – третьего, то при предъявлении ему первого и третьего элемента его вывод должен быть однозначен: «первый предпочтительнее третьего». Существует достаточно большое число способов выявления элементарных предпочтений. Каждый из известных способов выявления предпочтений одновременно является представителем способов получения информации от ЛПР или экспертов, поэтому каждый из них обладает определенными точностью, достоверностью, оперативностью и др. Рассмотрим наиболее употребительные методы выявления предпочтений. Непосредственное ранжирование. Этот способ выявления и выражения предпочтений заключается в расположении предъявленных элементов в порядке возрастания (так называемое прямое ранжирование) или убывания (обратное ранжирование) их предпочтительности. Каждому элементу в упорядоченном ряду приписывают натуральное число, называемое рангом элемента. В случае строгого ранжирования не допускается указывать на равноценность элементов и, следовательно, каждый элемент занимает свое отдельное место в ранжированном ряду и приобретает свой уникальный ранг. При нестрогом ранжировании несколько элементов могут занимать одинаковое место в ранжировке и получают одинаковый ранг. Заметим, что в терминах теории измерений ранжирование является измерением в порядковой шкале. Сама процедура проста и привычна для ее участников, что является ее несомненным достоинством. Будем считать, что, как это чаще всего и бывает, меньший ранг соответствует максимальной интенсивности проявления оцениваемого свойства (ранжирующего признака). Получаемая от эксперта информация представляется в виде оценок xij, имеющих значение от 1 до n. Если к процедуре привлечены m участников, то ранжирование по результатам их опроса определяется на осыраж упорядочения сумм рангов альтернатив, т.е. величин Таблица 3.1
Метод непосредственного ранжирования применяют обычно при числе ранжируемых объектов n £ 7±2 (значение 7±2 представляет собой так называемое «магическое число Миллера»). Это ограничение установлено психологами и определяется, как считают, объемом оперативной памяти человека. Если это условие не выполняется, достоверность результатов уменьшается, и целесообразно использовать другие методы. Парные сравнения – наиболее простой метод выявления отношений на множестве альтернатив, при котором проводящий эту операцию специалист сравнивает все объекты попарно, выявляя в каждой паре объект с более выраженным значением учитываемого при оценке отношения признака. Удобной формой представления получаемой от членов ГЭ информации является таблица парных сравнений (табл. 3.2). Таблицу заполняют следующим образом: если у объекта i значение ранжирующего признака лучше, чем у объекта j, то xij =1, а xji =0; при равенстве значений признака у сравниваемых объектах i и j xij = xji =0.5. Сумма элементов i -й строки таблицы парных сравнений Таблица 3.2
Существует и другой способ ранжирования, основанный на попарном сравнении, получивший название «медианный». Процедура ранжирования выполняется за ряд шагов. Вначале берут два любых элемента из множества и упорядочивают их. Затем берут третий элемент и сравнивают его с лучшим из первых двух, уже упорядоченных; если новый элемент лучше лучшего, то его «размещают» в упорядоченном ряду на первом месте; если он хуже лучшего, то его сравнивают с худшим и таким образом определяют его место. Затем берут следующий (четвертый) элемент и сравнивают его в паре с медианным элементом для построенного упорядоченного ряда из трех первых элементов, определяя «левый» или «правый» полуряд для дальнейшего уточнения места четвертого элемента и т. д. Попарное сравнение с градацией отношений было предложено американским ученым Т.Саати как составная часть метода анализа иерархий (МАИ). В этом методе выявления и описания отношений используется специальная шкала, характеризующая степень превосходства r ij объекта ai над объектом aj, при этом r ji = 1/ r ij. При равноценности, по мнению ЛПР, объектов ai и aj, значения r ij = r ji = 1. В случае слабого превосходства объекта ai над объектом aj r ij = 3, а r ji = 1/3. Если объект ai существенно важнее объекта aj, то r ij = 5 и r ji = 1/5, явно важнее – r ij = 7 и r ji = 1/7, а при абсолютном превосходстве r ij = 9 и r ji = 1/9. Допускается использовать и промежуточные (2, 4, 6, 8) значения r ij и, соответственно, r ji. Полученные оценки сводятся в матрицу R, для которой находится собственное значение, компоненты которого l i вычисляются как корень n -ой степени из произведения величин r ij в строке i матрицы. В качестве примера в табл. 3.3. приведены результаты использования этого метода для оценки отношений на множестве трех альтернатив. Таблица 3.3
Балльное оценивание. Оно заключается в том, что каждой альтернативе из множества предъявленных ставят в соответствие число (балл), характеризующее ее меру предпочтительности перед другими. Указанные числа (балльные оценки) выбирают из специальной балльной шкалы. Оценивание в балльной шкале рекомендуется проводить тогда, когда предпочтительность элемента устанавливается по строгим правилам, не допускающим неоднозначного толкования. При этом следует иметь в виду, что чем правила назначения баллов проще, размытее, тем ближе шкала балльных оценок (по своим свойствам и допустимым преобразованиям их значений) к порядковой. И наоборот, чем правила начисления баллов строже, точнее, детальнее, тем оценки в балльной шкале ближе по своим свойствам к интервальным. Это различие в шкалах следует особенно учитывать в случае привлечения к процедуре оценки отношений нескольких участников. При использовании порядковой балльной шкалы операция суммирования баллов, выставленных участниками процедуры, с целью получения результирующего ранжирования является математически не корректной, т.к. не определено начало шкалы и величины интервалов между рангами. Поэтому необходимо или использовать разрешенные в порядковой шкале операции нахождения средней величины (например, медианы), или принимать специальные меры для перехода к интервальной балльной шкале.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 79; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.195.30 (0.007 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

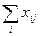 , при этом меньшая сумма определяет первый ранг и т.д. Полученная таким образом информация может быть представлена в виде табл. 3.1.
, при этом меньшая сумма определяет первый ранг и т.д. Полученная таким образом информация может быть представлена в виде табл. 3.1.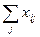 определяет место i -го объекта в упорядочении. Для примера в табл. 3.2 показаны результаты выявления методом парного сравнения отношения на множестве, состоящем из пяти альтернатив.
определяет место i -го объекта в упорядочении. Для примера в табл. 3.2 показаны результаты выявления методом парного сравнения отношения на множестве, состоящем из пяти альтернатив.