
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Отношения, их представление и свойстваСодержание книги
Поиск на нашем сайте
Выяснить, что такое отношение, наверное, проще всего на примерах. Рассмотрим несколько суждений, выражающих взаимосвязи между объектами: «Фирма А и фирма В являются производителями компьютеров»; «Фирма А основана раньше фирмы В»; «Порт Одесса южнее порта Калининград»; «Доллар США дороже российского рубля»; «В июне и сентябре по 30 дней». Несмотря на различия в указанных предложениях, можно заметить некоторые общие свойства в характере некоторых отношений. Так, отношения, утверждаемые первым и пятым предложениями, свидетельствуют о том, что некие два объекта принадлежат общему классу: в первом случае – фирм, выпускающих продукцию одного типа, во втором – месяцев продолжительностью в 30 дней. Во втором, третьем и четвертом отношениях общим является то, что они выражают некоторый порядок на множестве объектов. Во всех предложениях четко выражены названия объектов и отношений. Если использованные названия заменить другими, то возможны 3 ситуации: отношение останется справедливым, перестанет выполняться или потеряет смысл. Так, если в четвертое предложение вместо доллара США поставить евро, то отношение останется справедливым. Если в третьем предложении вместо Одессы поставить Мурманск, то отношение перестанет выполняться, а если в этом же третьем предложении вместо слов «порт Одесса» написать «доллар США», то выражение потеряет смысл. Следовательно, говорить об отношении можно только в том случае, когда выделено множество объектов, на которых это отношение определено. При принятии решений учитываются различные свойства объектов, и по этим свойствам отношения между одними и теми же объектами может быть разным. Это видно на примере первых двух из приведенных выше предложений. И еще один важный момент – часть отношений является отражением объективных свойств объектов (например, все приведенные выше), а часть может отражать субъективное мнение ЛПР. Например, утверждение «автомобили с автоматической коробкой передач удобнее автомобилей с ручной коробкой передач» отражает субъективное мнение автора этого высказывания, его личное отношение к автомобилям с разными типами коробок передач. Естественно, это субъективное отношение будет им учтено при принятии решения о покупке автомобиля наряду с объективными отношениями. Отношение может быть определено для любого количества объектов. Например, отношение «вкладчики Сбербанка России» выполняется для некоторого достаточно большого числа людей, обладающих всевозможными вкладами в соответствующем банке. Мы будем рассматривать только бинарные отношения, т.е. отношения, которые существуют или не существуют между двумя объектами из одного и того же множества. В дальнейшем под термином «отношение» мы будем понимать только бинарные отношения. Понятие «отношение» в математике служит для выражения на теоретико-множественном языке связей между объектами. Пусть X – заданное множество объектов. Отношением R на множестве X называется произвольноеподмножество R множества X ´ X, т.е. R Í X ´ X. Следовательно, задание R определяет, какие пары из множества X ´ X находятся в отношении R. Если пара < x, y > входит в R, т.е. < x, y >Î R, то пишут xRy, что читается: «x находится в отношении R с y». Для задания отношения < R, X > на множестве X надо указать все пары < x, y >Î X ´ X, которые содержатся в R, т.е. пары < x, y >Î X ´ X, для которых выполняется отношение R. Кроме непосредственного указания всех пар, для которых выполняется отношение R, существуют три основных формальных способа задания отношения: матрицей, графом или сечением. От того, как заданы отношения, зависят способы описания задачи выбора и представления требуемой информации. Наиболее часто и в самых разных приложениях используется задание отношений матрицей. Например, такое представление используется для отображения результатов турниров по спортивным играм, т.е. отношений между участниками турнира. Пусть X состоит из n элементов, пронумерованных целыми числами от 1 до n, R – отношение на X. Построим квадратную матрицу A (R) размером n ´ n, i -я строка которой соответствует i -му элементу множества X, обозначаемому как xi, а j -й столбец – j -му элементу, т.е. xj. На пересечении i -й строки и j -го столбца ставится 1, если выполнено xiRxj, и 0 – в противном случае. Обозначив через Aij элемент на пересечении i -й строки и j -го столбца, получим следующее общее правило задания матрицы отношения R:
1, если выполнено xiRxj,
0, если не выполнено xiRxj
Другой, геометрической, моделью отношения является граф. Граф может быть использован для представления отношения на небольшом числе элементов множества X. Пусть элементам множества X соответствуют вершины x 1, …, xn. Дуга от xi к xj существует, если выполнено xiRxj. Графовое представление отношения удобно в том случае, когда требуется математическая обработка информации, т.к. позволяет использовать богатый инструментарий теории графов. Задание отношения сечениями менее распространено, чем предыдущие, и мы не будем на нем останавливаться. Отношения между объектами не являются чем-то абстрактным, они зависят от ситуации принятия УР, т.е. от конкретного ЛПР, конкретного содержания проблемы и доступного для решения этой проблемы множества альтернатив. Действительно, в одной ситуации объект xi дороже объекта xj, а в другой их можно считать равноценными. Отношение между объектами определяется отношением к ним ЛПР, и именно это часто является решающим. Для принятия решения очень важным является рациональность отношений. Непосредственно рациональность оценить достаточно трудно. Поэтому для суждения о рациональности системы отношений между объектами и ЛПР рассматриваются некоторые достаточно простые свойства отношений. Отношение является рефлексивным, если для него справедливо xRx. Примерами являются отношения «быть похожим на», «стоить не больше». Отношение называют антирефлексивным, если оно выполняется лишь для несовпадающих объектов. Примерами являются отношения «быть дороже», «быть братом» (по отношению к сестре). Отношение называют симметричным, если оно включает в себя и обратное отношение. Иначе говоря, если выполнено xRy, то выполнено и yRx. Примеры – отношения «быть похожим на», «быть компаньоном». Для асимметричного отношения характерна несправедливость по меньшей мере одного из двух выражений – xRy или yRx. Заметим, что отношение «быть братом» не является ни симметричным, ни асимметричным. Действительно, если Петр брат Павла, то Павел брат Петра, но если Петр брат Елены, то Елена не является братом Петра. Если отношение R асимметрично, то оно антирефлексивно. Если выражения xRy и yRx справедливы одновременно только тогда, когда x = y, то отношение R является антисимметричным. Для принятия решений очень важными свойствами отношения является транзитивность и ацикличность. Отношение R транзитивно, если из xRy, yRz следует xRz. Отношение R называется ацикличным, если из xRz 1, z 1 Rz 2, …, zn -1 Ry следует x ¹ y. Транзитивность и ацикличность отношений играют важную роль в теории выбора, т.к. отражают некоторые естественные, рациональные взаимосвязи между объектами выбора. Действительно, если x в каком-то смысле лучше y, а y в том же смысле лучше z, то естественно считать, что в этом же смысле x лучше, чем z (транзитивность), и, во всяком случае, x не хуже y (ацикличность). Рассмотренные свойства позволяют определить некоторые отношения, используемые в дальнейшем. Отношение R называется эквивалентностью, если оно рефлексивно, симметрично и транзитивно. Обычно такое отношение обозначают символом ~. Очевидно, что задание эквивалентности на некотором множестве объектов равносильно заданию разбиения этого множества на классы эквивалентных друг другу элементов, и, наоборот, некоторое разбиение множества определяет задание соответствующей ему эквивалентности. Но задание разбиения не задает упорядочения. Для определения некоторого упорядочения, т.е. задания в каком-то смысле порядка на множестве элементов, вводятся отношения порядка. Нестрогим упорядочением (отношением нестрогого порядка) называется отношение, обладающее свойствами рефлексивности, антисимметричности и транзитивности. Для обозначения нестрогого порядка обычно используют символ p. Отношение, обладающее свойствами антирефлексивности, асимметричности и транзитивности, называется строгим упорядочением (отношением строгого порядка). Для обозначения строгого порядка используют символp. По нестрогому порядку можно найти соответствующий строгий порядок, и наоборот. Действительно, если p - нестрогий порядок, то ему можно сопоставить строгий порядокp, определяемый следующим образом: x p y, когда x p y и x ¹ y. Наоборот, если p - строгий порядок, ему можно сопоставить отношение p таким образом: x p y, когда x p y или x = y. Поэтому используется термин частичный порядок, понимая под ним нестрогий порядок. Частичный порядок называют линейным, если для любых x, y выполняется одно из трех условий: x p y, x = y, x f y. Строгий порядок является частным случаем отношения доминирования, которое не обладает свойством транзитивности и ацикличности. Отношение доминирования характеризует, например, отношения на множестве команд – участниц турнира по спортивным играм. В основе рассмотренных отношений лежит представление о полезности объектов, причем областью значений функции полезности является множество действительных чисел. В тех случаях, когда каждый объект отношения характеризуется m показателями, и определить полезность каждого варианта в виде одного действительного числа затруднительно, отношение между вариантами определяется отношениями между этими m показателями. Отметим два вида возникающих в этом случае отношений, широко используемых при принятии решений. Пусть xj, yj – значение j -го показателя варианта x и y соответственно. Отношением Парето (P) называют отношение [ xPy ]Û {(" j = 1, m) [ xj f yj ] и ($ j 0 Î{1,…, m })[ xj f yj ]}. Таким образом, объект x находится с объектом y в отношении Парето, если для всех пар показателей существует отношение частичного порядка, и хотя бы для одной – строгого. Иначе: объект x находится с объектом y в отношении Парето, если он по всем показателям не хуже, но хотя бы по одному строго лучше. Пусть на множестве показателей задан линейный порядок, такой, что k 1 > k 2 >…> km, где ki – номер показателя на i -м месте порядка. Отношением лексикографии (L) называют отношение [ xLy ] Û [ xk 1 f yk1], или [ xk 1 ~ yk 1 и xk 2 f yk 2 ], или … и [ x ¹ y ]. Следовательно, объекты находятся в отношении лексикографии, если для первой пары показателей имеется отношение строгого порядка, или для этой пары существует отношение эквивалентности и одновременно для второй пары имеется отношение строгого порядка, и т.д. Отношения Парето и лексикографии относятся к типу бинарных отношений, получивших название координатных, для сравнения по которым достаточно иметь информацию об отношениях знаков разностей одноименных показателей, или координат критериального пространства, с чем связано название отношения. Важным свойством отношений Парето и лексикографии является рациональность. Оно, в частности, означает, что из отношения xPy или xLy следует превосходство варианта x над вариантом y хотя бы по одному показателю. Это свойство указанных отношений обусловливает их широкое использование при принятии рациональных решений.
|
||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 91; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.179.120 (0.012 с.) |

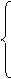
 A (R) = Aij (R) = (i, j = 1, n).
A (R) = Aij (R) = (i, j = 1, n).


