
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет параметров движения покоординатным сглаживанием методом нвк по данным локацииСодержание книги
Поиск на нашем сайте
Для обеспечения расчетов определим проекции собственного пути на неподвижные оси координат Начало неподвижной системы координат совпадает с местоположением судна-наблюдателя в момент первого замера с направлением осей Nord, Ost. Проекции пути собственного судна на момент i-го измерения на неподвижные оси будут:
где i- номер замера.
Определение параметров траектории методом наименьших квадратов начинается со времени получения 3-его замера. Рассмотрим метод наименьших квадратов в общем виде. Пусть имеется функция
В нашем случае
где
Необходимо минимизировать евклидову норму вектора невязок с учетом весов измерений.
Здесь N - число измерений
Введем векторы и матрицы
Если ввести вектор Введем
Раскроем поэлементно обращение матрицы В. Если L=B-1, то
Определим проекции дистанции и скорости объекта методом наименьших квадратов на момент последнего измерения.
В нашем случае оценке методом наименьших квадратов подвергаются координаты в неподвижной системе координат
Запишем матрицы B и С в явном виде для двух координат:
Рассчитаем элементы ковариационной матрицы Cov{qN} методом наименьших квадратов на момент последнего измерения. Получим следующее выражение:
После расчета вектора Х по формуле (4.42), используя формулы (2.15),(2.16), (2.17)-(2.20), вычисляем значения курса, скорости объекта и их дисперсий. Списки исходных, используемых алгоритмом параметров, и параметров, определяемых в результате решения задачи, которые необходимы для составления алгоритма по данному математическому описанию, приведены в таблицах 4.3 и 4.4.
Таблица 4.3 Используемая информация
Таблица 4.4 Результаты решения задачи
ЗАДАНИЕ К ПРАКТИЧЕСКОМУ ЗАНЯТИЮ
1. По приведенным выше соотношениям составить блок-схему модуля расчета оценок параметров движения объекта наблюдения, ковариаций и дисперсий ошибок оценивания.
2. Используя модульный принцип построения программ, построить блок-схему модели исследования алгоритма, приведенного в данной главе. Блок-схема должна включать в себя модули: - движения наблюдателя (см. приложение 2), - движения объекта наблюдения (см. приложение 2), - расчета истинных значений дистанций и пеленгов, - упрощенных моделей функционирования систем гидролокации или радиолокации, обеспечивающих имитацию случайных гауссовых ошибок измерения (см. приложение 3) и наложение ошибок на истинные значения измеряемых параметров для моделирования измеренных значений П и D, - модуль расчета оценок ПДО и их расчетных дисперсий, - модуль вычисления статистических ошибок оценивания при повторении N раз моделируемого процесса (см. приложение 3). Структурная схема модели приведена в приложении 1.3.
3. Разработать программу статистического исследования алгоритма на языке программирования, заданном преподавателем.
4. Рассчитать вручную контрольные варианты. Провести отладку и тестирование программы.
5.Провести на компьютере машинный эксперимент в соответствии с заданными исходными данными моделирования. Оформить пояснительную записку, включающую программную документацию и результаты исследования.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

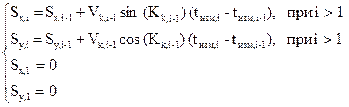 (4.36)
(4.36)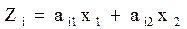
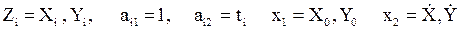
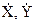 - скорости изменения X, Y,i - номер измерения, hi=Zi + dhi –измеренное значение Zi; dhi - ошибка измерения, X0,Y0 - начальные значения X и Y.
- скорости изменения X, Y,i - номер измерения, hi=Zi + dhi –измеренное значение Zi; dhi - ошибка измерения, X0,Y0 - начальные значения X и Y.
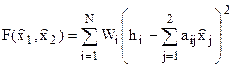
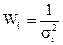 ,
, 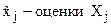
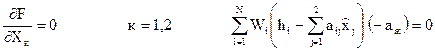
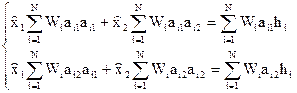
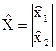 ,
, 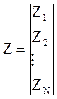 ,
,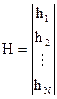 ,
, 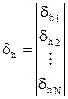 ,
, 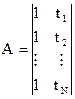 ,
, 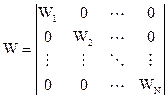 , тогда
, тогда 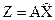 ; H = Z+dh H;
; H = Z+dh H; 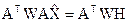
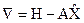 , то
, то 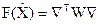
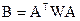 и
и 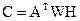 , тогда
, тогда 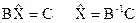
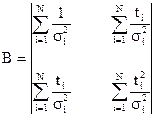
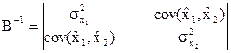
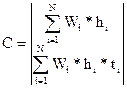
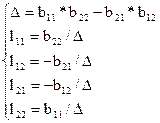
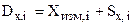 ,
, 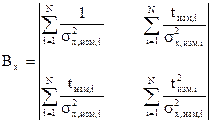 (4.37)
(4.37)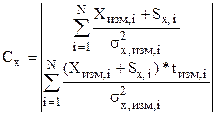 , (4.38)
, (4.38)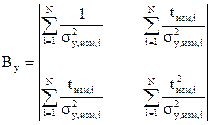 , (4.39)
, (4.39)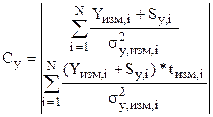 , (4.40)
, (4.40)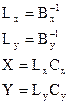 , (4.41)
, (4.41) 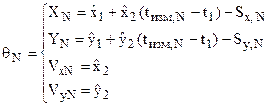 (4.42)
(4.42)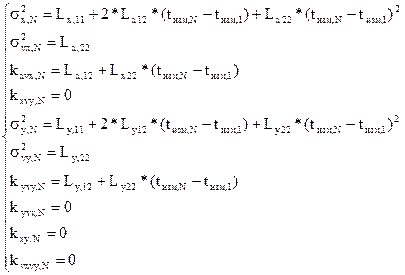 (4.43)
(4.43)


