Метод двух замеров дистанции

 

             

Излагаемый метод предполагает поступление в ИУС последовательностей замеров пеленгов П _I на объект наблюдения   и дистанций D_I, полученных либо посредством гидролокации или радиолокации, где I- номер замера, принимающий значения от 1 до N.

          Первый поступивший замер   [П ₁, D ₁ ] фиксируется и используется в качестве первого замера в расчетах. В качестве второго замера принимается последний поступивший замер.

Для оценки точности определения КПДО используются значения среднеквадратичных ошибок (СКВО) измерения пеленга s _П и дистанции s_D.  Измерения пеленга и дистанции считаются некоррелированными между собой:   

 

                        Cov { П _I, D _I } = 0.                                (2.1)

 

 Предполагается, что поступление замеров происходит через интервалы времени, обеспечивающие отсутствие автокорреляции замеров каждой из величин во времени: 

                                  

               Cov { П _I-1, П _I } = 0, Cov { D _I-1, D _I } = 0. (2. 2)

 

 

     Исходные данные для использования данного метода определения КПДО перечислены в таблице в конце раздела.

 

       Алгоритм расчета предполагает равномерное прямолинейное движение объекта наблюдения, при этом K _O = const, V _O = const. По данным двух замеров [П ₁, D ₁ ],  [П ₂, D ₂ ] определяются значения проекций V _X,V_Y  скорости объекта наблюдения на неподвижные оси координат  X,Y. 

      Для выполнения этих расчетов сначала определяются значения проекций пути собственного судна на оси координат X,Y:

                  

    S _X =  S_XO + ò _O^TV _S (t) sin К _S dt =

                                      = S_XO + V _{S, I-1} sin К _S-1 (t _I - t _I-1),          

                                                                                                   (2.3)

     S_Y = S _YO + ò _O^TV _S (t) sin К _S dt=

                                      = S _YO + V _{S, I-1} sin К _S-1 (t _I - t _I-1),

 

            Проекции скорости объекта на оси координат находятся по следующим формулам:

 

                 V _X = (D_Xj + S_Xj - D_Xi - S_Xi) / (t_j - t_i);

                                                                                                  (2.4)

                 V _Y = (D_Yj + S_Yj - D_Yi - S_Yi) / (t_j - t_i);

 

где   j, i - номера замеров (j > i),

                        

                   D_Xi = D _i sin П _i;     D_Xj = D _j sin П _j ;

                                                                                                   (2.5)

                   D _Yi = D _i cos П_i ; D _Yj = D _j cos П _j .

 

           Дисперсии проекций V _X,V_Y  скорости объекта на оси координат Var { V_Y } = s²_Vy, Var { V _X } = s²_Vx   определяются с помощью аппарата преобразований с линейными функциями случайных величин. Формулы их расчета представлены ниже:

 

Var { V _X } = (Var {D_Xj } + Var{ D_Xi }) / (t_j - t_i) ²;

                                                                                                      (2.6)

Var { V_Y } = (Var { D_Yj} + Var { D_Yi }) / (t_j - t_i) ² .

 

             Ковариационный момент между V _X,V_Y   в соответствии с аппаратом линейных преобразований со случайными величинами и исходя из формул  (2.4) и  (2.5), а также условия некоррелированности замеров во времени опишем следующим выражением:

 

Cov {V _X V_Y} = (Cov {D_Xj D_Yj} + Cov{ D_Xii D_Yi }) / (t_j - t_i) ²   (2.7)

            Дисперсии и ковариационные моменты проекций D_Xj D_XiD_Y D_yi замеренных дистанций на оси координат определим опираясь на формулы (2.5). Зависимости проекций замеренных дистанций от величин замеров [П ₁, D ₁ ] являются нелинейными. Проведем их линеаризацию в точках со значениями, равными значениям замеров. Получим следующие приближенные уравнения:

 

 D_Xi ^*» D_Xi  + ¶ D_Xi / ¶ D _i * (D- D _i) + ¶ D_Xi / ¶ П _i * (П - П _i);

                                                                                                    (2.8)

 D_Yi ^*» D_Yi  + ¶ D_Yi / ¶ D _i * (D- D _i) + ¶ D_Yi / ¶ П _i * (П - П _i);

 

где D_Xi ^*, D_yi ^* - значения проекций дистанции в точках отклонений от замеров, D_Xi, D_Yi - значения проекций дистанции в точках замеров, П ₁, D ₁ - значения замеров, П, D,  - значения замеряемых параметров с отклонениями.

 

Тогда, учитывая, что   

                  ¶ D_Xi / ¶ D _i = sin П _i

                   ¶ D_Yi / ¶ D _i = cos П _i

                                                                                                  (2. 9)

                  ¶ D_Xi / ¶ П _i =  D _j cos П _j

                  ¶ D_Yi / ¶ П _i = -  D _i sin П _i

 

получим следующие зависимости:

 

Var {D_XI } = (¶ D_Xi / ¶ D _i) ² Var {D_I }+

                                                 + (¶ D_Xi / ¶ П _i) ²  Var {П_I };

                                                                                                  (2.10)

Var { D_YI} = (¶ D_Yi / ¶ D _i) ²  Var {D_I } +

                                                 + (¶ D_Yi / ¶ П _i) ²  Var {П_I };

              

или 

 

Var {D_XI } = (sin П _ii) ² Var {D_I }  + (D _j cos П _j) ²  Var {П_I };

                                                                                                (2.11)

Var { D_YI} =(cos П _i) ²  Var {D_I } + (D _i sin П _i ) ²  Var {П_I };

 

Значения ковариационного момента определятся по следующей формуле:

 

Cov {D_X D_Y} = ¶ D_Xi / ¶ D _i* ¶ D_Yi / ¶ D _i* Var {D_I } 

                   + ¶ D_Xi / ¶ П _i * ¶ D_Yi / ¶ П _i* Var {П_I } =

                   =  (sin П _i cos П _i ) Var {D_I }  +

                   + (D _j ² cos П _j sin П _ii)   Var {П_I }.           (2.12)

         Значения курса К и скорости  V объекта наблюдения оцениваются с помощью следующих соотношений:

 

              V = Ö (V _X ² + V_Y ² )                                    (2.13)

         

    ì Priv _2p (Arctg (V _X / V_Y ))  , если V_Y > 0;

    ï Priv _2p (p + Arctg (V _X / V_Y )), если V_Y < 0;

K = í                                                                                   (2. 14)

    ï p / 2, если V_Y = 0 и V _X > 0;

    î 3p / 2,      если V_Y = 0 и V _X  < 0;

 

 где Priv _2p - процедура приведения угла к интервалу [ 0; 2p), рассмотренная в приложении 3.

 

           Для вычисления дисперсий ошибок оценивания нелинейных функций V и K снова воспользуемся аппаратом линеаризации. Функции скорости и курса объекта представим в следующем виде:

 

         V = V ^* + ¶ V/ ¶ V _X * (V _X - V _X^* )

                         + ¶ V / ¶ V_Y  * (V_Y - V_Y ^*   );          (2.15)

 

         K = K ^* + ¶ K/ ¶ V _X * (V _X - V _X^* ) 

                         + ¶ K / ¶ V_Y  * (V_Y - V_Y ^*  );          (2.16)

 

где V ^*, K ^*  - оценочные значения скорости и курса объекта, V, K -  возможные значения скорости и курса объекта, которые мы описываем распределением случайных величин относительно полученных оценок.

 

         Значения производных в формулах (2.15) и (2.16) рассчитываются по приведенным ниже формулам:

 

  ¶ V/ ¶ V _X = V _X / Ö (V _X ² + V_Y ² ) = V _X / V; 

                                                                                              (2.17)

  ¶ V / ¶ V_Y = V_Y / Ö (V _X ² + V_Y ² ) = V_Y / V;

 

 

   ¶ K/ ¶ V _X = V_Y / V ² ;

                                                                                               (2.18)

   ¶ K / ¶ V_Y  = -V _X / V ²;

 

    Используя уравнения (2.15) и (2.17) и применяя методы определения дисперсий линейных функций случайных величин, получим следующие расчетные формулы дисперсии оценки скорости Var { V^*} и курса Var { K^*}  объекта:

 

Var { V^*} = (V ^* _X / V^* ) ²  * Var { V _X } + (V ^* _Y / V^* ) ²  * 

            * Var { V _Y } + 2* (V ^* _X * V ^* _Y / V^{* 2} ) *Cov { V _X^*  V_Y ^*}; 

                                                                                                 (2. 19)

           

Var { K^*} = (V ^* _Y / V^{* 2} ) ²  * Var { V _X } + (V ^* _X / V^{* 2} ) ²  *  

            * Var { V _Y } - 2* (V ^* _X * V ^* _Y / V^{* 4} ) * Cov { V _X^*  V_Y ^*};

                                                                                                 (2. 20)

 

где символ ^* обозначает оценку соответствующего параметра.

 

Для построения алгоритма на основе приведенного выше математического описания необходимо выделить величины, которые известны перед началом решения задачи. Эти величины представляют информацию, используемую алгоритмом.

Результатом решения задачи будут рассчитанные значения других величин. Списки исходных, используемых алгоритмом параметров, и параметров, определяемых в результате решения задачи приведен в таблицах 2.1 и 2.2.

 

Таблица 2.1                                        Используемая информация

№	Величина	Обозначение
1.	Замеры дистанции до объекта, м	DI
2.	Замеры пеленга на объект, град	ПI
3.	СКВО измерений дистанции, м	sD
4.	СКВО измерений пеленга, град	sП
5.	Собственный курс управляющего судна, град	КS
6.	Собственная скорость управляющего судна, м/с	VS
7.	Интервал времени между I- ми замерами, сек	D t I

 

Таблица 2.2                                      Результаты решения задачи

№	Величина	Обозначение
1.	Проекция скорости на ось Х, м/c	V X
2.	Проекция скорости на ось Y, м/c	V Y
3.	Скорость, м/c	V
4.	Курс, рад	K
5.	Дисперсия проекции скорости на ось Х, м^2/c^2	Var { V X }
6.	Дисперсия проекции скорости на ось Y, м^2/c^2	Var { VY }
7.	Ковариация проекций скорости на оси, м^2/c^2	Cov {V X VY}
8.	Дисперсия скорости,, м^2/c^2	Var { V^*}
9.	Дисперсия курса, рад^2	Var { K^*}

 

ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ

 

1. По приведенным выше соотношениям составить блок-схему модуля расчета оценок параметров движения объекта наблюдения и дисперсий ошибок оценивания.

2. Используя модульный принцип построения программ, построить блок-схему модели исследования приведенного в данном разделе алгоритма. Блок-схема должна включать в себя следующие модули:

-движения  наблюдателя (см. приложение 2),

-движения объекта наблюдения (см. приложение 2),

-расчета истинных значений дистанций и пеленгов,

-упрощенных моделей функционирования систем гидролокации или радиолокации, обеспечивающих имитацию случайных гауссовых ошибок измерения (см. приложение 3) и наложение ошибок на истинные значения измеряемых параметров для моделирования измеренных значений П и D, 

-расчета оценок ПДО и их расчетных дисперсий,

-вычисления статистических ошибок оценивания при повторении N раз моделируемого процесса (см. приложение 3).

Структурная схема модели приведена в приложении 1.1.

 

3. Разработать программу статистического исследования алгоритма на языке программирования, заданном преподавателем. В рамках исследования должны быть сравнены расчетные и статистические ошибки оценивания параметров движения объекта.

 

4. Рассчитать вручную контрольные варианты. Провести отладку и тестирование программы.

 

5. Провести на компьютере машинный эксперимент в соответствии с заданными исходными данными моделирования. Оформить пояснительную записку, включающую программную документацию и результаты исследования.

 

МЕТОД ЧЕТЫРЕХ ПЕЛЕНГОВ

 

В ряде случаев в ИУС могут поступать только последовательности замеров пеленга П _I на объект наблюдения,  полученных посредством гидроакустического пеленгования шумящего объекта.

          Первый поступивший замер   [П ₀,] фиксируется и используется в качестве нулевого замера в расчетах. Для оценки точности определения КПДО используются значения среднеквадратичных ошибок измерения пеленга s_п..Предполагается, что поступление замеров происходит через временные интервалы, обеспечивающие отсутствие автокорреляции замеров во времени. В связи с этим, измерения пеленга считаются некоррелированными между собой: 

                                  

               Cov { П _I-1, П _I } = 0. (3.1)

 

Исходные данные для использования этого метода определения КПДО представлены в конце раздела.

 

    Алгоритм расчета предполагает равномерное прямолинейное движение объекта наблюдения. При этом K _O = const, V _O = const.

      Для выполнения расчетов определяются значения проекций пути собственного судна на оси координат X,Y:

              

    S _X =  ò _O^TV _S (t) sin К _S (t) dt =

                                      = S_I=1 ^N V _{S, I} sin К _S,I (t _I - t _I-1),          

                                                                                                   (3.2)

   S_Y =  ò _O^TV _S (t) sin К _S (t) dt =

                                      = S _I=1 ^N V _{S, I-1} sin К _S,I (t _I - t _I-1),

 где V _S (t), К _S (t) - текущие значения скорости и курса наблюдателя,

траектория наблюдателя, представляющая собой движение несколькими (N) галсами, каждый из которых представляется участком равномерного прямолинейного движения со скоростью V _{S, I} курсом К_S,I  в течение времени t _I - t _I-1, I- номер галса.

 

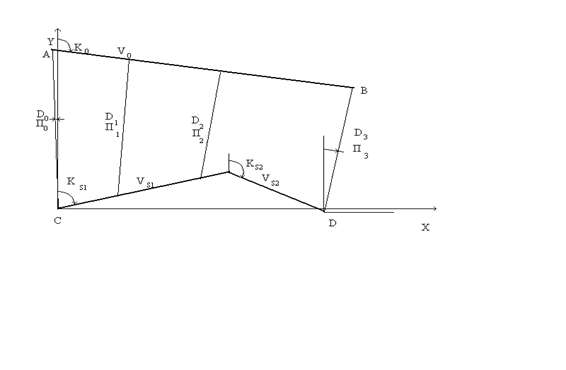
Для построения алгоритма расчета рассмотрим взаимное движение наблюдателя и объекта наблюдения, изображенное на рис.3.1

Рис.3.1

 

На рис.3.1 обозначены: траектория АВ- траектория объекта наблюдения, принимается гипотеза прямолинейного равномерного движения объекта, СD - траектория наблюдателя, СА- дистанция до объекта наблюдения в момент нулевого замера, DB- дистанция до объекта в момент текущего замера.

 Введя векторы, соединяющие точки начала и конца указанных траекторий, составим следующее векторное уравнение:

 

­CA+ ­AB= ­CD+­DB,                                                              (3.3)

 

где ­CA - обозначение вектора, исходящего из точки С в точку А.

Проектируя уравнение (3.3) на оси декартовой системы координат получим следующие уравнения:

 

D₀ sin П₀ + V₀ sin K₀ (t_I - t₀ ) = S _X + D_i sin П_i,

(3.4)

D₀ cos П₀ + V₀ cos K₀ (t_I- t₀ ) = S _Y + D_i cos П_i,

 

где D₀ - дистанция до объекта наблюдения в момент нулевого замера t₀, D_i - дистанция до объекта в момент t_I текущего i-ого замера,V₀, K₀ -скорость и курс объекта.

В данной системе уравнений неизвестными являются D₀, V₀, K₀ и D_i.

При этом величины V₀ и K₀  представлены в уравнениях нелинейными зависимостями. Перейдем к линейному виду, введя вместо значений скорости и курса объекта значения проекций скорости объекта на оси координат:

 

 V_ox= V₀ sin K₀ , V_oy= V₀ cos K_0.                                                                           (3.5)

 

Сократим количество неизвестных путем объединения уравнений в одно уравнение. Для этого умножим первое уравнение на cos П_i, а второе на sin П_i.

Вычтя из первого уравнения второе, получим следующее уравнение:

 

D₀ sin П₀ cos П_i + V_0X cos П_i (t_I - t₀ ) - D₀ cos П₀ sin П_i –

- V_0Y sin П_i(t_I- t₀ ) = S _X cos П_i -S _Y sin П_i                                          (3.6)

 

Введем обозначения:

a_I = sin П₀ cos П_i - cos П₀ sin П_i= sin (П₀ - П_i ),

b_I = cos П_i (t_I - t₀ ),

c_I =- sin П_i(t_I- t₀ ),

h_I= S _X cos П_i -S _Y sin П_i .

 

Получим следующее уравнение:

 

a_I D₀ + b_I V_0X + c_I V_0Y = h_I                                                                (3.7)

 

Уравнение (3.7) строится по двум замерам: нулевому и i-ому.

Для того, чтобы используя уравнение (3.7) определить искомый вектор [D_{0 ,} V_0X, V_0Y], включающий три переменные, необходимо составить систему трех уравнений:

 

a₁ D₀ + b₁ V_0X + c₁ V_0Y = h₁,

a₂ D₀ + b₂ V_0X + c₂ V_0Y = h₂,                                                          (3.8)

a₃ D₀ + b₃ V_0X + c₃ V_0Y = h_3.

 

 Первое уравнение строится по замерам пеленгов П₀ и П₁ , второе - по замерам П₀ и П₂ , третье - по замерам П₀ и П_3.

Всего для решения системы уравнений (3.7) необходимо получить четыре замера пеленга: (П₀ , П₁, П₂ и П₃). Потому метод назван методом четырех пеленгов.

 

Решением системы уравнений (3.7) является следующее выражение:

 

X = A ^-1 *B,                                                         (3.9)

 

где А и В - матрицы коэффициентов:

 

       a₁,b₁, c₁

А = a₂, b₂, c_2  ,                                                                         (3.10)

       a₃, b₃, c₃

 

       h₁

В =  h₂    ,.                                                                               (3.11)

       h₃

 

       D₀

X = V_0X      .                                                                               (3.12)

       V_0Y

.

Решение имеет место, когда детерминант матрицы А не равен нулю. Это условие выполняется, если система уравнений является линейно независимой. Система уравнений является линейно зависимой, когда объект и наблюдатель двигаются прямолинейно равномерно. Для устранения линейной зависимости уравнений наблюдатель должен совершить хотя бы одно изменение направления движения, т.е. его траектория должна включать не менее двух галсов.

После определения вектора Х (3.12) требуется рассчитать значения курса и скорости объекта, используя, при этом, формулы (2.13) и (2.14).

Для построения алгоритма на основе приведенного выше математического описания необходимо выделить величины, которые известны перед началом решения задачи. Эти величины представляют информацию, используемую алгоритмом.

Результатом решения задачи будут рассчитанные значения других величин. Списки исходных, используемых алгоритмом параметров, и параметров, определяемых в результате решения задачи, приведены в таблицах 3.1 и 3.2.

 

Таблица 3.1                               Используемая информация

	Величина	Обозначение
1.	Замеры пеленга на объект, град	ПI
2.	СКВО измерений пеленга, град	sПI
3.	Собственный курс управляющего судна, град	КS
4.	Собственная скорость управляющего судна, м/с	VS
5.	Момент времени I- ого замера, сек	t I

 

 

Таблица 3.2                                      Результаты решения задачи

№	Величина	Обозначение
1.	Начальная дистанция до объекта, м	D0
2.	Проекция скорости на ось Х, м/c	V X
3.	Проекция скорости на ось Y, м/c	V Y
4.	Скорость, м/c	V
5.	Курс, рад	K

 

 

ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ

 

1. По приведенным выше соотношениям составить блок-схему модуля расчета оценок параметров движения объекта наблюдения.

1. Используя модульный принцип построения программ, построить блок-схему модели исследования приведенного в данном разделе алгоритма. Блок-схема должна включать в себя следующие модули:

-движения  наблюдателя (см. приложение 2),

-движения объекта наблюдения, (см. приложение 2)

-расчета истинных значений пеленгов,

- упрощенных моделей функционирования систем гидроакустического измерения пеленга, обеспечивающих имитацию случайных гауссовых ошибок измерения (см. приложение 3) и наложение ошибок на истинные значения измеряемых параметров для моделирования измеренных значений П  , 

-расчета оценок ПДО,

-вычисления статистических ошибок оценивания при повторении N раз моделируемого процесса (см. приложение 3).

Структура модели приведена приложении 1.2.

 

2. Разработать программу статистического исследования алгоритма на языке программирования, заданном преподавателем. В рамках исследования должны быть сравнены расчетные и статистические ошибки оценивания параметров движения объекта.

 

3. Рассчитать вручную контрольные варианты. Провести отладку и тестирование программы.

 

4.  Провести на компьютере машинный эксперимент в соответствии с заданными исходными данными моделирования. Оформить пояснительную записку, включающую программную документацию и результаты исследования.