
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Закон эквивалентов. Газовые законы
Закон постоянства состава позволил установить количественные соотношения, в которых различные химические элементы соединяются между собой, Д. Дальтон ввёл в науку понятие о соединительных весах элементов, впоследствии названных эквивалентами. В настоящее время химическим эквивалентом называют реальную, формульную или условную частицу вещества, которая может замещать, присоединять, высвобождать или быть каким либо другим способом эквивалентна одному иону водорода в кислотно-основных или ионообменных реакциях. Один химический эквивалент равен или в целое число раз меньше чем формульная единица. Эквивалентное число вещества Х, Z(X) показывает, сколько химических эквивалентов содержится в одной формульной единице вещества. Фактор эквивалентности [feq(X)] вещества Х показы-вает, какая часть формульной единицы вещества является химическим эквивалентом: feq(Х) = 1/Z(X). Например: Z(HCl) = 1, feq(HCl) = 1, а Z(H2SO4) = 2, feq(H2SO4) = ½. Молярная масса эквивалентов вещества Х [M eq (Х)] —это масса одного моля эквивалентов. Имеет размерность г/моль. Молярный объем эквивалентов газообразного вещества Х [Veq(Х)] — это объем одного моля его эквивалентов. Имеет размерность л/моль. Количество эквивалентов вещества Х [n[feq(X)] можно определить соотношением: n[feq(X)] = m(X)/M[feq(X)] = m(X)/feq(X)·M(X) где m — масса вещества Х, M[feq(X)] — молярная масса эквивалентов вещества Х, M(X) — молярная масса вещества Х. Введение в химию понятия эквивалент позволило сформулировать закон эквивалентов: вещества вступают в реакцию в количествах, пропорциональных их эквивалентам. При решении некоторых задач удобно пользоваться другой формулировкой закона: массы реагирующих веществ пропорциональны их эквивалентным массам. Определение молекулярной и атомной массы. Некоторые методы определения молекулярных масс Закон Авогадрооткрывает путь для экспериментального определения молекулярных масс газов и веществ, переходящих в газообразное состояние без разложения. Пусть число молекул в заданном объёме сравниваемых газов составляет N. Если массу молекулы первого газа обозначить за m1, а массу молекулы второго газа — m2, то массы одинаковых объёмов при одинаковых условиях будут относиться, как молярные массы. Это третье следствие из закона Авогадро.
Отношение массы данного объёма газа к массе такого же объёма другого газа называется плотностью одного газа по второму и обозначается буквой D: D2(1) = m1/m2, Принимая во внимание, что молярная масса пропорциональна молекулярной: M = 6,02·1023·m получаем: D2(1) = M1/M2. Плотность D газа показывает во сколько раз один газ тяжелее другого. Если известны плотность D2(1) первого газа по второму и молярная масса M(2) второго газа, то можно вычислить молярную массу M(1) первого газа: M(1) = D2(1)·M(2). Обычно плотность газа определяют по водороду или по воздуху, вводя соответственно обозначение DH2(X) или Dвозд.(X). Если известна плотность газа X по водороду, то M(X) = DH2·M(H2), а так как молярная масса водорода округленно равна 2, то М(X) = 2·DH2(X). Если известна плотность газа по воздуху, средняя молярная масса которого принимается равной 29, то искомая молярная масса газа M(X) = 29·Dвозд.(X). Пример 3. Вычислить молярную массу монооксида азота, плотность которого по водороду равна 15. М(NO) = 2·15 = 30 г/моль. Пример 4. Вычислить молярную массу бутана, если его плотность по воздуху равна 2. М(С4Н10) = 2·29 = 58 г/моль. Для определения молярной массы газа можно использовать представление о его молярном объёме. Моль любого газа при нормальных условиях (н. у.) занимает объём 22,4 л. Следовательно, если известна масса m(X) некоторого объёма V газа X при н. условиях, то M(Х) = 22,4·m(X)/V(X) г/моль. Пример 5. Вычислить молярную массу этана 5,6 л которого при нормальных условиях имеют массу 7,5 г. х = Зная молярную массу газа легко вычислить его плотность по водороду, воздуху или любому другому газу, молярная масса которого известна. Пример 6. Вычислить плотность по водороду гемиоксида азота. DH2(N2O) = Пример 7. Найти плотность по воздуху тетрафторида кремния. Dвозд. (SiF4) = Измерения объёмов газов обычно проводят в условиях отличных от нормальных. Для приведения объёма газа к нормальным условиям используют уравнение объединенного газового закона:
В этом уравнении V — объём данной массы газа при заданных давлении p и температуре T (в Кельвинах); V0 — объём этой же массы газа при нормальных условиях (при давлении 101325 Па и температуре 273 К).
Если V0 означает объём, занимаемый при нормальных условиях, 1 моль газа при н.у. занимает объем 22,4 л, то для всех газов соотношение В Интернациональной системе единиц (СИ) давление выражается в Паскалях (Па, 1 Па = 1 Н/м2), объём в кубических метрах (м3), следовательно значение универсальной газовой постоянной определяется значением (рассчитаем его для одного моля газа при н.у.): R = В практике химических исследований объём и давление часто выражают в единицах других систем: объём — в литрах или миллилитрах, давление — в атмосферах или миллилитрах ртутного столба. Для перевода результатов измерений в единицы СИ пользуются соотношениями: 1 атм. = 760 мм рт. ст. = 101325 Па; 1 мм рт. ст. = 1,31·10-3 атм. = 133,322 Па. Если давление р0 выражено в атмосферах, а объём V0 — в литрах, то: R = Для случая, когда р0 выражено в миллиметрах ртутного столба, а объём V0 — в миллилитрах, получим: R = Подставим в уравнение
Для n моль газа это уравнение приобретает следующий вид: pV = nRТ Это уравнение получило название: уравнение Клапейрона - Менделеева. Учитывая, что число молей газа n равно отношению массы газа к его молярной массе, т. е. n = m/M, уравнение Клапейрона-Менделеева часто применяют в виде: р·V = Для использования уравнения Клапейрона-Менделеева удобно вначале умножить обе его части на M, тогда: pVM = mRT и далее из него легко находятся любые величины. Уравнение Клапейрона-Менделеева позволяет рассчитать молярную массу, а следовательно и молекулярную массу любого вещества, находящегося в газообразном состоянии: M = Пример 8. Вычислить молекулярную массу диэтилового эфира, если 215 мл его паров при 77 °С и давлении 700 мм рт. ст. имеют массу 0,51 г. M = Молярная масса диэтилового эфира равна 74 г/моль, следовательно, его молекулярная масса 74 а. е. м. Пример 9. Найти молекулярную массу оксида углерода (IV), если 73,3 г его при 27 °С находясь в сосуде ёмкостью 10 л, создают давление 4,1 атм.: М = Следовательно молекулярная масса диоксида углерода равна 44 а. е. м. §7.2.5. Некоторые методы определения атомных масс химических элементов Метод Авогадро. Закон Авогадро позволяет определить молекулярные массы газов. С другой стороны, результаты изучения объёмных соотношений газов, вступающих в реакцию, и полученных газообразных продуктов позволяют определить число атомов в молекуле. Так, при взаимодействии одного объёма хлора с одним объёмом водорода образуются два объёма хлороводорода. Из этого следует, что молекула хлора, как и молекула водорода, состоит из двух атомов. Аналогично было установлено, что молекулы других простых газов, таких как кислород, азот, также двухатомны. Атомную массу перечисленных газов находят делением их молекулярной массы на два. Например, молекулярная масса хлора равна 71, следовательно его атомная масса 35,5.
О количестве атомов, входящих в состав молекул, можно также судить по их молярной теплоёмкости. Именно по результатам измерения этой характеристики благородных газов было установлено, что их молекулы одноатомны и атомная масса этих газов равна их молекулярной массе. Метод Канниццаро. Метод применим для определения атомных масс элементов, дающих газообразные или легколетучие соединения. Для нахождения атомной массы этим методом определяют молярную массу возможно большего числа газообразных или легколетучих соединений данного элемента. Затем на основании данных анализа рассчитывают, сколько атомных единиц массы приходится на долю этого элемента в молекуле каждого из взятых соединений. Наименьшее количество данного элемента в молекуле изученных веществ и будет его атомной массой, так как в молекуле не может находиться меньше одного атома. В таблице приведены молекулярные массы ряда соединений углерода, процентное содержание углерода в каждом из них, а также масса углерода, содержащаяся в 1 моль каждого из этих соединений. Молекулярные массы некоторых углеродсодержащих соединений и содержание в них углерода.
Наименьшая масса углерода, содержащегося в моле приведённых соединений равна 12 а. е. м. Следовательно атомная масса углерода не может быть больше 12 (иначе пришлось бы предположить, что в состав сероуглерода, диоксида и монооксида углерода входит часть атома углерода). Считать атомную массу углерода меньше 12, также нет оснований, так как соединения, содержащие менее 12 а. е. м. углерода, неизвестны. Метод Менделеева. Атомную массу элемента можно рассчитать, исходя из положения этого элемента в Периодической системе. Приблизительную атомную массу элемента можно вычислить, как среднеарифметическое атомных масс соседних с ним элементов. Так, атомная масса алюминия, рассчитанная как среднеарифметическое атомных масс магния, кремния, бора и скандия:
вполне удовлетворительно согласуется с табличной величиной 26,98. Разделив приблизительное значение атомной массы элемента на молярную массу его эквивалента, находят валентность элемента, округлив её до целочисленного значения, и затем, умножая эквивалентную массу на валентность элемента, находят его точную атомную массу.
Метод, основанный на законе Дюлонга и Пти. Французские учёные П. Дюлонг и А. Пти установили закон, согласно которому атомная теплоемкость простого вещества в твердом состоянии (т. е. произведение его удельной теплоемкости на молярную массу вещества) есть величина постоянная и равная в среднем 26 Дж/(К·моль). Из закона Дюлонга и Пти следует, что разделив 26 на удельную теплоёмкость простого вещества, легко определяемую экспериментально, можно найти приблизительное значение атомной массы данного элемента. Чтобы перейти от приблизительного значения атомной массы к точному её значению, предварительно определяют опытным путём эквивалентную массу данного элемента. Разделив приблизительное значение атомной массы на молярную массу его эквивалента, находят валентность элемента, часто несколько отличающуюся от целого числа. Так как валентность выражается только целыми числами, найденное значение округляют. Умножив эквивалентную массу на валентность, получают точное значение мольной массы атомов. Пример 10. Определить молекулярную массу металла, удельная теплоёмкость которого равна 0,226 Дж/(г·К), а его оксид содержит 21,23% кислорода. Вычислим приблизительное значение молярной массы атомов металла М(Ме)» значение эквивалентной массы металла: 21,23:78,77 = 8:х х = 78,77·8 / 21,23 = 29,68 (г/моль) и валентность металла:
Так как валентность может выражаться только целым числом, полученное значение округляем до 4. Умножая эквивалентную массу на валентность, вычислим точное значение молярной массы атомов металла: 29,68 · 4 = 118,70 (г/моль) По Периодической системе находим, что это олово.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.105.124 (0.03 с.) |
|||||||||||||||||||||||||||||||||||||||||||||
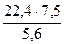 = 30 г.
= 30 г.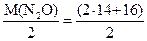 = 22
= 22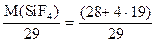 = 3,59.
= 3,59.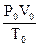 =
= 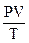
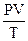 будет постоянной величиной. Эта величина называется универсальной газовой постоянной, обозначается буквой R, имеет размерность: единица энергии/(Кельвин·моль). Численное значение R зависит от единиц, в которых выражается объём и давление газа.
будет постоянной величиной. Эта величина называется универсальной газовой постоянной, обозначается буквой R, имеет размерность: единица энергии/(Кельвин·моль). Численное значение R зависит от единиц, в которых выражается объём и давление газа.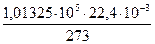 = 8,314 Дж/(К·моль).
= 8,314 Дж/(К·моль).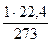 = 0,082 л·атм./(К·моль).
= 0,082 л·атм./(К·моль).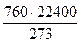 = 62360 мл·мм рт. ст./(К·моль).
= 62360 мл·мм рт. ст./(К·моль).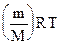 .
.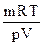
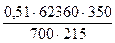 = 74 г/моль
= 74 г/моль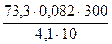 = 44 г/моль.
= 44 г/моль.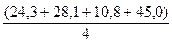 = 27,05
= 27,05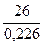 = 115 г/моль
= 115 г/моль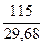 = 3,87
= 3,87


