
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные формулы комбинаторикиСодержание книги
Поиск на нашем сайте Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов). Как при решении задач с использованием классического определения вероятности, так и в дальнейшем нам понадобятся некоторые формулы комбинаторики. Приведем наиболее употребительные из них. Размещениями из n различных элементов по m элементов (m ≤ n) Например, из трех элементов a, b, c можно составить по два элемента следующие размещения: ab, ac, bc, ba, ca, cb Число размещений из n элементов по m элементов определяется по формуле:
Пример 2.1. В высшей лиге чемпионата по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами? Решение: Если размещения из n элементов взяты по n (т.е. отличаются только порядком расположения элементов), то такие размещения называются перестановками - Р n . Перестановки можно считать частным случаем размещений при m = n. Следовательно, число всех перестановок из n элементов вычисляется по формуле:
Пример 2.2. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз. Решение: Искомое число трехзначных чисел Р3=3!=6. Сочетаниями из n различных элементов по m элементов Другими словами, если из всех размещений, которые можно составить из n элементов по m, отберем только те, которые одно от другого отличаются хотя бы одним элементом, то получим число сочетаний из n элементов по m элементов. Число сочетаний из n элементов по m элементов вычисляется по формуле:
Отметим особенность формулы (2.3): Пример 2.3. На тренировках занимаются 12 баскетболистов. Сколько может быть организовано разных стартовых пятерок? Решение: Пример 2.4. В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных. Решение: Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь m деталей из N деталей, т.е. Тогда вероятность того, что среди отобранных деталей ровно k стандартных равна: .
|
||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

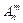 называются упорядоченные выборки, объемом m элементов, отобранные из n элементов, которые отличаются либо самими элементами, либо порядком расположения элементов.
называются упорядоченные выборки, объемом m элементов, отобранные из n элементов, которые отличаются либо самими элементами, либо порядком расположения элементов.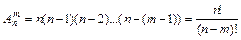
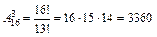 способами
способами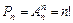
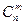 называются неупорядоченные выборки объемом m элементов из n элементов, которые отличаются хотя бы одним элементом.
называются неупорядоченные выборки объемом m элементов из n элементов, которые отличаются хотя бы одним элементом.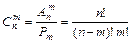
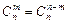 . Этим свойством удобно пользоваться, когда m > n /2.
. Этим свойством удобно пользоваться, когда m > n /2.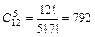 .
.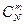 . Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди m деталей ровно k стандартных): k стандартных деталей можно взять из n стандартных деталей
. Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди m деталей ровно k стандартных): k стандартных деталей можно взять из n стандартных деталей 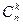 способами; при этом остальные m-k деталей должны быть нестандартными; взять же m-k нестандартных деталей из N-n нестандартных можно
способами; при этом остальные m-k деталей должны быть нестандартными; взять же m-k нестандартных деталей из N-n нестандартных можно 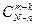 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 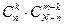 .
.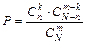 .
.


