
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теория вероятностей и математическая статистикаСодержание книги
Поиск на нашем сайте Программа, методические указания и контрольные задания для студентов заочной формы обучения технических специальностей
Воркута
2014 УДК 517.523(075.83) ВЫСШАЯ МАТЕМАТИКА. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА: Программа, методические указания и контрольные задания /Воркутинский филиал Ухтинского государственного технического унверситета. Сост.: Булдакова Е.Г., Даль Н.Н., Черемушкина О.И., 2014.
Методические материалы предназначены для оказания помощи студенту при самостоятельном изучении IV части курса высшей математики в соответствии с учебным планом для технических специальностей. Предложены контрольные задания, самостоятельное выполнение которых необходимо для успешного изучения курса. Методические указания могут быть использованы студентами всех форм обучения.
Табл.18, Ил. 17.
Научный редактор: проф. А.П. Господариков
Введение Теорией вероятностей называется раздел математики, изучающий закономерности массовых (т.е. повторяющихся многократно) случайных явлений. Теория вероятностей является основой методов математической статистики, которые используются при обработке результатов исследований. Изложенный в методических указаниях материал соответствует учебной программе: 1. Случайные события. Основные понятия теории вероятностей. 2. Вероятность суммы событий. 3. Вероятность произведения событий. 4. Формула полной вероятности и формула Байеса. 5. Повторение независимых опытов и теоремы Лапласа. 6. Теорема Бернулли и закон Пуассона. 7. Случайные величины. Закон распределения и функция распределения. 8. Математическое ожидание случайной величины. 9. Дисперсия и среднее отклонение случайной величины. 10. Показательный закон распределения и закон Пуассона. 11. Равномерный и нормальный законы распределения. 12. Система двух случайных величин. Закон и функция распределения. 13. Условный закон распределения и условное математическое ожидание. 14. Начальные и центральные моменты случайной величины и системы случайных величин. Коэффициент корреляции. 15. Выборка и эмпирическое распределение. Графическое представление. 16. Точечные оценки параметров распределения по эмпирическим данным. 17. Интервальные оценки параметров распределения по эмпирическим данным. 18. Понятие о критерии согласия. Критерий Пирсона χ2. 19. Статистическая и корреляционная связь. Уравнения прямых регрессий.
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ Наблюдаемые нами события могут быть трех видов: достоверные, невозможные и случайные. Событие называется достоверным, если в результате данного опыта оно обязательно произойдет. Например, извлечение белого шара из урны, содержащей только белые шары. Событие невозможное, если в результате данного испытания оно произойти не может, например, извлечение белого шара из урны, содержащей черные шары. Событие называется случайным, если в результате данного опыта оно может либо произойти, либо не произойти. Например, попадание в цель при выстреле из орудия. Два события А и В называются несовместными, если они не могут произойти вместе при одном и том же испытании. Два события А и В называются совместными в данном опыте, если появление одного из них не исключает возможность появления другого. Группа событий А1, А2, … А n называется группой несовместных событий, если события, входящие в группу, попарно несовместны. Группа событий называется группой совместных событий, если совместны хотя бы два события из этой группы. События А1, А2, … А n называют единственно возможными, если при испытании обязательно произойдет только одно из этих событий. События А1, А2, … А n образуют полную группу событий, если они являются единственно возможными и несовместными исходами некоторого испытания. Например, бросают монету. Событие А1 – выпадение герба, А2 – выпадение решки. События А1 и А2 образуют полную группу событий. События А1, А2, … А n называются равновозможными, если нет оснований полагать, что одно из этих событий является более возможным, чем другие. Количественной мерой возможности появления рассматриваемого события является вероятность. Наиболее широкое распространение получили определения вероятности события: классическое, геометрическое и статистическое. Классическое определение вероятности связано с понятием благоприятствующего исхода. Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события. Вероятность события А равна отношению числа благоприятствующих исходов к общему числу равновозможных и несовместных исходов:
где m – число благоприятствующих событию А исходов; n – общее число возможных исходов. Из определения вероятности события следуют её простейшие свойства:
1. Вероятность достоверного события равна единице:
2. Вероятность невозможного события равна нулю: 3. Вероятность случайного события выражается положительным числом, которое меньше единицы. Так как для случайного события 0< m < n, то Пример 1.1. Монету подбросили 1 раз. Какова вероятность появления герба. Решение: Пример 1.2. В урне 5 белых и 7 черных шаров. Вынули 1 шар. Какова вероятность, что он белый? Решение: Классическое определение вероятности дает возможность рассматривать лишь события, которые распадаются на конечное число равновероятных исходов. Это недостаток классического определения вероятности. Рассмотрим понятие вероятности события для случаев с бесконечным множеством исходов испытания. Пусть на плоскости имеется область G и некоторые области g в ней. Их площади равны соответственно SG и Sg. В область G бросается наугад точка. Вероятность того, что точка окажется в области g принимается равной Статистическое определение вероятности связано с понятием относительной частоты появления события А в опытах. Относительная частота появления события А вычисляется по формуле:
где m 1 - число появлений события А в серии из n 1 опытов (испытаний). Вероятностью события А называется число относительно которого стабилизируется (устанавливается) относительная частота В практических задачах за вероятность события А принимается относительная частота
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 109; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

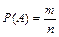 ,
,
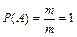 .
.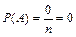 .
.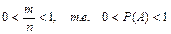 .
.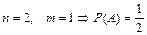
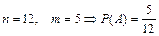
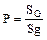 . При этом предполагается, что точка может попасть в любую часть области G, а вероятна лишь её площадь и не зависит ни от расположения, ни от формы области. Вероятность, определенная по такой схеме, называется геометрической.
. При этом предполагается, что точка может попасть в любую часть области G, а вероятна лишь её площадь и не зависит ни от расположения, ни от формы области. Вероятность, определенная по такой схеме, называется геометрической.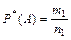 ,
,
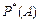 при неограниченном увеличении числа опытов.
при неограниченном увеличении числа опытов.


