
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка статистических гипотез
Условимся называть статистической гипотезой всякое предположение о виде закона распределения некоторого признака генеральной совокупности. Проверку правильности или неправильности выдвинутой гипотезы проводят статистическими методами с помощью критерия согласия. Под критерием согласия подразумевают совокупность условий, подтверждающих справедливость принятой гипотезы. В результате такой проверки может быть принято правильное или неправильное решение. Поэтому при оценке согласованности выдвинутой гипотезы возможны ошибки двух типов: если отклоняется правильная гипотеза и если принимается ложная гипотеза. Ошибки первого типа относятся к ошибкам первого рода; ошибки второго типа – к ошибкам второго рода. Вероятность ошибки первого рода обычно обозначают через α и называют уровнем значимости критерия согласия. Вероятность ошибки второго рода обозначают через β. Величину (1 -β), т.е. вероятность того, что будет отвергнута ошибочная гипотеза, называют мощностью критерия. Для проверки справедливости гипотезы о законе распределения случайной величины используют несколько критериев, различных по мощности и методу обработки исходных данных, из которых наиболее распространенными являются критерий Колмогорова и критерий χ2 (хи-квадрат) Пирсона. Первый используется в случае, когда параметры распределения известны до опыта и требуется после опыта проверить согласованность теоретического и экспериментального распределения, второй – при неизвестных параметрах распределения. Для применения критерия χ2 при оценивании согласия теоретического и статистического распределений вариационный ряд эмпирических значений разбивают на k равных интервалов. Число значений ряда в интервале (эмпирическая частота) обозначают буквой ni. Зная границы каждого интервала и принятый закон распределения, можно найти вероятность попадания случайной величины в этот интервал р i. После этого из формулы
Полученное значение χ2 сравнивают с критическим значением
Гипотезу о предполагаемом законе распределения считают справедливой при условии Пример 9.1. По полученным в результате измерений данным (табл.9.1.) проверить гипотезу о нормальном распределении генеральной совокупности.
Таблица 9.1.
Решение: Вычисляем среднее значение интервала Для того чтобы вычислить теоретические вероятности попадания случайных величин в интервалы (xi, xi+1), на основании таблиц функции Лапласа находим значения Ф(zi) и Ф(zi+1). После этого составляем еще одну таблицу для расчета теоретических частот (табл.9.2) Таблица 9.2
Составляем таблицу для определения Таблица 9.3
Число степеней свободы r =9-3=6, по уровню значимости a=0,05 и r =6 из таблицы распределения c2 находим
Задачи теории корреляции Функциональной зависимостью называется такая связь между переменными величинами, при которой зависимая величина - функция - полностью определяется значениями влияющих независимых величин - аргументов. Вид зависимости между аргументами и функцией обычно задается в виде формулы. Наиболее часто на практике используются: линейная функция y = ax + b, гиперболическая Корреляционная зависимость - это такая связь между величинами, когда определенным значениям влияющих величин - факторов соответствуют множество значений зависимой величины, распределенных по известному закону распределения. Например, чем больше товарооборот x, тем больше должна быть сумма издержек обращения y (x), однако, если фактические данные о товарообороте и издержках, полученных от разных потребительских обществ, нанести в виде точек на координатную плоскость (x, y), то они могут иметь вид прямолинейного вытянутого облака -корреляционного поля (рис.10.1.)
При определении корреляционной зависимости, решаются две задачи: 1. установить форму корреляционной зависимости, т.е. вид функции; 2. оценить тесноту (силу) корреляционной связи (она оценивается по величине рассеяния значений y вокруг условного среднего
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.126.80 (0.011 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
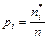 находится теоретическая частота появления события
находится теоретическая частота появления события 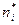 . Для определения меры расхождения по критерию χ2 используют выражение:
. Для определения меры расхождения по критерию χ2 используют выражение: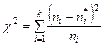
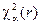 этого критерия. Значение
этого критерия. Значение 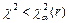 . Если
. Если 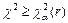 , гипотезу отвергают.
, гипотезу отвергают.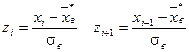
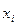
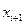
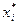
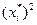
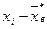
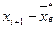
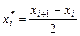 и находим
и находим 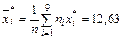 .Далее находим
.Далее находим 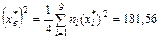 . Используя для выборочной дисперсии формулу
. Используя для выборочной дисперсии формулу 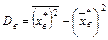 , находим D в =181,56-159,52=22,04. Отсюда
, находим D в =181,56-159,52=22,04. Отсюда 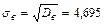 .
.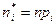
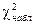 (табл.9.3)
(табл.9.3)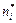
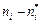
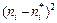
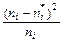
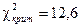 . Так как
. Так как 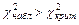 , то гипотеза отвергается, следовательно, требуется либо изменить вид закона, либо повторить опыты.
, то гипотеза отвергается, следовательно, требуется либо изменить вид закона, либо повторить опыты.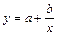 , показательная -
, показательная - 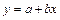 , степенная (обычно парабола) -
, степенная (обычно парабола) - 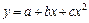 .
. Под корреляционной зависимостью y от x понимается зависимость условной средней
Под корреляционной зависимостью y от x понимается зависимость условной средней 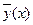 от x, т.е.
от x, т.е. 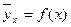 . Это равенство называется уравнением регрессии y на х. Вместе с регрессией y на х всегда может быть построена и регрессия x на y, с уравнением
. Это равенство называется уравнением регрессии y на х. Вместе с регрессией y на х всегда может быть построена и регрессия x на y, с уравнением 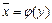 .
.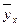 . Чем меньше рассеяние, тем сильнее корреляционная зависимость).
. Чем меньше рассеяние, тем сильнее корреляционная зависимость).


