
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительная вероятность, доверительные интервалы
Средняя выборочная, выборочные дисперсия и среднее квадратическое отклонение являются оценками параметров генеральной совокупности, выражающимися одним числом. Такие оценки называются точечными. Они зависят от объема выборки и могут сильно отличаться от истинной величины оцениваемого параметра, т.е. приводят в некоторых случаях к грубым ошибкам. Это вызывает необходимость оценивать точность и надежность полученных по выборке точечных оценок, что производится при помощи интервальных оценок. Оценкой математического ожидания а (или, что то же самое В таком случае ε можно считать точностью оценки. В силу случайности вариант, попадающих в выборку, говорить о выполнении неравенства Эту запись следует понимать так: вероятность того, что Если заранее известна величина ε, то границы доверительного интервала для оценки математического ожидания имеют вид: Пример 8.1. Выборочное обследование бюджета 36 семей выявило средний доход в месяц на одну семью в 3000 рублей. Найти доверительный интервал для оценки математического ожидания а - среднемесячного дохода всех 10 тысяч исследуемых семей, если известно, что он распределен по нормальному закону со средним квадратическим отклонением σ=250 руб. Величина доверительной вероятности γ, принять равной 0,9. Решение: Найдем значение аргумента t функции Лапласа из соотношения:
Доверительная вероятность связана не с величиной параметра а, а лишь с границами интервала, которые изменяются при изменении выборки. Надежность γ=0,9 указывает на то, что если произведено достаточно большое число выборок, то 90% из них определяет такие же интервалы, в которых параметр а действительно заключен и лишь в 10% случаев он может выйти за границы доверительного интервала. Если среднее квадратическое отклонение исследуемого признака заранее неизвестно, то используется его выборочная оценка σв - эмпирическое отклонение, определяемое по данным выборки. В этом случае доверительный интервал а для имеет вид:
Пример 8.2. Найти доверительный интервал для оценки с надёжностью 0,95 неизвестного математического ожидания a нормально распределенного признака Х генеральной совокупности, если выборочное среднее квадратическое σв =1,4, выборочное среднее Решение: Найдем величину tγ. По таблице распределения Стьюдента для n =16и γ = 0,95 находим доверительные границы. Нижняя граница: Верхняя граница: Итак, с надежностью 0,95 неизвестный параметр а заключен в интервале 9,86 < а <11,34. Наряду с доверительной вероятностью используется понятие уровня значимости, обозначаемое обычно через α. Связь между этими величинами задается соотношением γ+ α=1.
Наряду со средним квадратическим отклонением в качестве характеристики рассеяния вариант выборки около среднего выборочного, иногда используется среднее абсолютное отклонение Δ, определяемое формулой:
Пример 8.3. По данным статистического распределения выборки найти выборочное среднее, квадратическое отклонение σв и среднее абсолютное отклонение Δ.
Решение:
В экономическом анализе важной характеристикой выборки является коэффициент вариации v, определяемый по формуле: Коэффициент вариации служит для сравнения величин рассеяния двух вариационных рядов. Тот из радов, у которого коэффициент вариации больше, имеет большее рассеяние.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 50; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.177.223 (0.005 с.) |
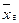 - генеральная средняя) какого-либо количественного признака Х генеральной совокупности служит выборочная средняя
- генеральная средняя) какого-либо количественного признака Х генеральной совокупности служит выборочная средняя 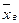 . Очевидно, что
. Очевидно, что 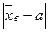 . Иначе говоря, если выбрать положительное число ε>0, и записать неравенство
. Иначе говоря, если выбрать положительное число ε>0, и записать неравенство 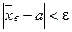 , то
, то 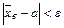 , можно, лишь с некоторой вероятностью γ, которая называется надежностью или доверительной вероятностью оценки, т.е. Р (
, можно, лишь с некоторой вероятностью γ, которая называется надежностью или доверительной вероятностью оценки, т.е. Р (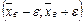 заключает в себе (покрывает) неизвестное математическое ожидание а равна γ, а сам интервал
заключает в себе (покрывает) неизвестное математическое ожидание а равна γ, а сам интервал 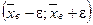 называется доверительным интервалом.
называется доверительным интервалом.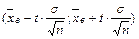 , где
, где 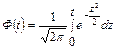 из соотношения
из соотношения 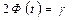 с заранее выбранной доверительной вероятностью γ.
с заранее выбранной доверительной вероятностью γ.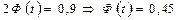 и по таблице значений функции Лапласа находим t=1,645. Тогда точность оценки равна
и по таблице значений функции Лапласа находим t=1,645. Тогда точность оценки равна 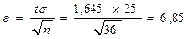 . Таким образом, значения неизвестного параметра а согласующееся с данным выборки, удовлетворяет неравенству 179,15 < а <192,85.
. Таким образом, значения неизвестного параметра а согласующееся с данным выборки, удовлетворяет неравенству 179,15 < а <192,85.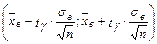 , где
, где 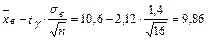 .
.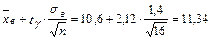 .
.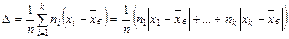
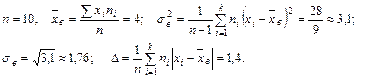
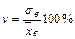 .
.


