Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение результирующей операционной погрешности
Определение суммарной погрешности может осуществляться двумя методами: расчётно-аналитическим и статистическим.
7.1 Расчётно-аналитический метод определения суммарной погрешности При использовании данного метода придерживаются следующего порядка расчёта: 1. Выявляют перечень факторов, приводящих к появлению первичных погрешностей - износ, жёсткость, температура и т.п. 2. Определяют значения первичных погрешностей от влияния каждого фактора. При этом главная задача - определение полей рассеивания. 3. Выясняют законы распределения погрешностей (закон нормального распределения, Симпсона, равной вероятности и др.) 4. Суммируют найденные значения с учётом законов их распределения: - случайные погрешности суммируют в соответствии с законом распределения (если он известен); - погрешности, подчиняющиеся нормальному закону распределения - суммируют по правилу квадратного корня; - погрешности, не подчиняющиеся закону распределения, суммируют алгебраически. - систематические постоянные погрешности суммируются алгебраически, но с учётом знака. В общем случае, для суммарной погрешности, можно применить следующую формулу:
где w п i - постоянная для данной партии погрешность; k å - суммарный коэффициент относительного рассеивания первичных погрешностей; k 1, k 2, k 3,…, ki - коэффициенты относительного рассеивания отдельных составляющих погрешностей, которые показывают степень отличия принятого закона распределения каждой погрешности от закона нормального распределения. Аналитический метод является достаточно трудоёмким, громоздким, требует знания законов распределения отдельных погрешностей, что не всегда возможно, и, поэтому, он является недостаточно точным.
7.2 Статистический метод определения суммарной погрешности Этот метод базируется на теории вероятностей и математической статистике. Имеет две разновидности: метод кривых распределения и метод точностных диаграмм.
Метод кривых распределения
Используется как в массовом, так и в серийном производствах. Метод заключается в следующем: из партии обработанных заготовок выбирается группа, проводятся замеры геометрических параметров, и выполняется статистический анализ. При статистическом анализе необходимо соблюдать следующие условия:
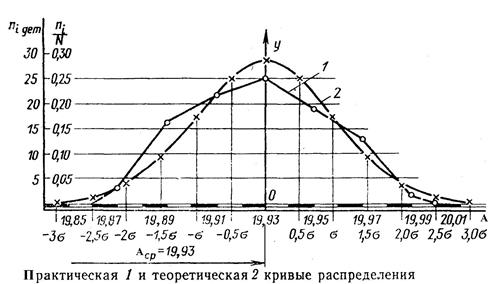
1. Для анализа берут детали, обработанные одним режущим инструментом или между двумя подналадками станка. 2. Измерение проводят измерительным инструментом с ценой деления не превышающей (1/6…1/10) Т. 3. Число деталей, взятых для статистического анализа должно быть достаточно большим (желательно 50 и более, но не меньше 20 деталей). Рассмотрим алгоритм определения суммарной погрешности обработки: 1. Производится обработка парии N деталей на настроенном оборудовании в автоматическом цикле. 2. Выполняется замер анализируемого геометрического параметра. 3. Строится практическая кривая распределения. Для этого определяются: - размах варьирования: R = Amax - Amin; - число интервалов К, которое зависит от размеров партии (при N £50 … 100 шт., К=5…7); - размер интервала С = R / К; - частота попадания размеров в каждый интервал ni; - координаты середины интервалов Аср i. - строится практическая кривая распределения (рисунок 26). 4. Строится теоретическая кривая распределения (в большинстве случае это кривая Гаусса). Её построение выполняют в следующем порядке:
Рисунок 26 – Кривые распределения - определяется координата центра группирования размеров (средний размер) и среднее квадратичное отклонение по формулам:
- определяются координаты у для характерных точек кривой Гаусса ± s, ± 2 s, ± 3 s; - строится кривая Гаусса 5. Определяется суммарная погрешность. Для этого определяются: -погрешность от случайных и закономерно изменяющихся факторов Δр. =6 s; - постоянная погрешность, вызванная неточностью настройки станка, Δн. =|Аср. – АТср.|; - суммарная погрешность Δ å = 2Δн. + Δр. Возможны следующие случаи расположения кривой относительно поля допуска: 1. Δ å < Т, Δн. =0 - обработка обеспечивает заданное качество; 2. Δ å < Т, Δн. ≠ 0 - требуется поднастройка станка; 3. Δ å > Т, - возможно появление брака. Брак может быть не исправимый и исправимый. Метод имеет следующий недостаток: полученная погрешность характеризует точность законченного процесса, а влияние случайных и закономерно изменяющихся факторов оценивается совместно, что не даёт возможности прогнозировать изменение точности в процессе дальнейшей обработки.
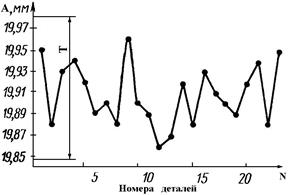
Раздельно определить влияние на точность случайных и закономерно изменяющихся погрешностей позволяет метод точностных диаграмм. Метод точностных диаграмм Используются три вида диаграмм: точечные диаграммы, диаграммы групповых средних и точностные диаграммы хода технологического процесса. Точечные диаграммы По горизонтальной оси откладываются номера деталей, последовательно обрабатываемых на станке, по вертикали - получаемые размеры (рисунок 27). Диапазон колебаний размеров показывает степень влияния случайных факторов, а тенденция к изменению размеров говорит о наличии закономерно изменяющегося фактора.
Рисунок 27 – Точечная диаграмма
Определяя размах варьирования R=Аmax-Аmin, путём сопоставления с заданным допуском Т судят о стабильности хода технологического процесса.
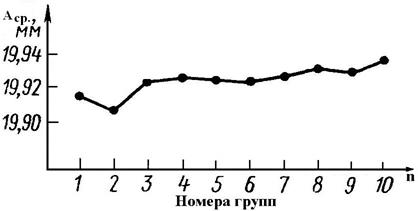
Диаграммы групповых средних Строится в тех же координатах, только по оси абсцисс откладываются номера групп обрабатываемых деталей, а по оси ординат - средние размеры заготовок, входящих в группу (рисунок 28):
где m –число заготовок, входящих в группу (4 и более заготовок). Например, Аср.1 = (А1+А2+ А3+А4) /4, Аср.2 = (А5+А6+А7+А8)/4.
Рисунок 28 – Точностная диаграмма групповых средних
На этой диаграмме колебания случайных погрешностей резко уменьшаются за счёт осреднения, зато влияние закономерно изменяющихся погрешностей проявляется более наглядно и объективно. По данной диаграмме можно определить тенденцию изменения размеров во времени под влиянием такого закономерно-изменяющегося фактора, как износ режущего инструмента.
|
||||||
|
Последнее изменение этой страницы: 2021-04-05; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.9.146 (0.009 с.) |
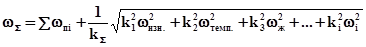 ,
,
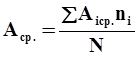 ,
, 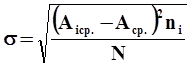 ;
;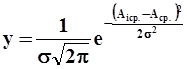 .
.
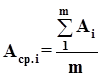 ,
,