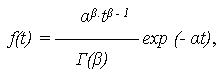Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические модели теории надежности. Общие понятия о моделях надежностиСодержание книги
Поиск на нашем сайте
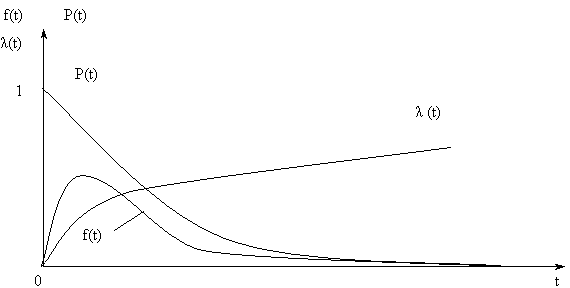
Общие понятия о моделях надежности Для решения задач по оценке надежности и прогнозированию работоспособности объекта необходимо иметь математическую модель, которая представлена аналитическими выражениями одного из показателей P(t) или f(t) или Выясним, как изменяется безотказность объектов при их эксплуатации, что позволит классифицировать модели и определить возможности их применения. Опыт эксплуатации показывает, что изменение интенсивности отказов
Рис. 1
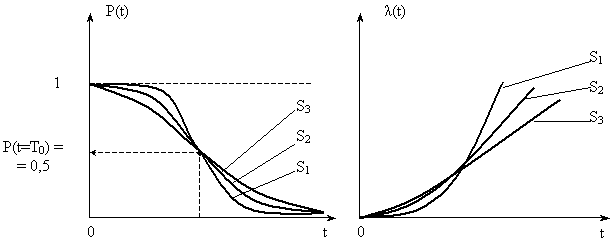
Кривую можно условно разделить на три характерных участка: первый – период приработки, второй – период нормальной эксплуатации, третий – период старения объекта. Период приработкиобъекта имеет повышенную интенсивность отказов ИО, вызванную приработочными отказами, обусловленными дефектами производства, монтажа, наладки. В период нормальной эксплуатации ИО уменьшается и практически остается постоянной, при этом отказы носят случайный характер и появляются внезапно, прежде всего из-за несоблюдения условий эксплуатации, случайных изменений нагрузки, неблагоприятных внешних факторов и т. п. Именно этот период соответствует основному времени эксплуатации объекта. Возрастание ИО относится к периоду старения объекта и вызвано увеличением числа отказов от износа, старения и других причин, связанных с длительной эксплуатацией. Вид аналитической функции, описывающей изменение показателей надежности P(t), f(t) или Выбор закона распределения Выбор закона распределения состоит в подборе аналитической функции наилучшим образом аппроксимирующей эмпирические функции надежности. Выбор, в значительной мере, процедура неопределенная и во многом субъективная, при этом многое зависит от априорных знаний об объекте и его свойствах, условиях работы, а также анализа вида графиков Очевидно, что выбор распределения будет зависеть, прежде всего, от вида эмпирической функции ПРО Предположим, что по тем или иным соображениям, выбран гипотетический закон распределения, заданный теоретической ПРО
где a, b, c, … - неизвестные параметры распределения. Требуется подобрать эти параметры так, чтобы функция f(t) наилучшим образом сглаживала ступенчатый график На графике вместе с Расчет критерия согласия Критерий согласия – это критерий проверки гипотезы о том, что случайная величина T, представленная своей выборкой, имеет распределение предполагаемого типа. Проверка состоит в следующем. Рассчитывается критерий, как некоторая мера расхождения теоретического и эмпирического распределений, причем эта мера является случайной величиной. Чем больше мера расхождения, тем хуже согласованность эмпирического распределения с теоретическим, т. е. меньше мала, то гипотезу о выборе закона распределения следует отвергнуть, как мало правдоподобную. В противном случае – экспериментальные данные не противоречат принятому распределению. Из известных критериев наиболее применяемый критерий согласия - рассчитывается критерий
где - определяется число степеней свободы R = k – L, где L – число независимых условий, наложенных на частоты а) условие б) условие совпадения в) условие совпадения Чаще всего L = 3. Чем больше число степеней свободы, тем больше случайная величина - по рассчитанным Ответ на вопрос: насколько мала должна быть вероятность P, чтобы отбросить гипотезу о выборе того или иного закона распределения – во многом неопределенный. На практике, если P < 0,1, то рекомендуется подыскать другой закон распределения. В целом, с помощью критерия согласия, можно опровергнуть выбранную гипотезу, если же P достаточно велика, то это не может служить доказательством правильности гипотезы, а указывает лишь на то, что гипотеза не противоречит данным эксперимента. 1. Классическое нормальное распределение Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым. Считается, что наработка подчинена нормальному распределению (нормально распределена), если плотность распределения отказов (ПРО) описывается выражением:
где a и b – параметры распределения, соответственно, МО и СКО, которые по результатам испытаний принимаются:
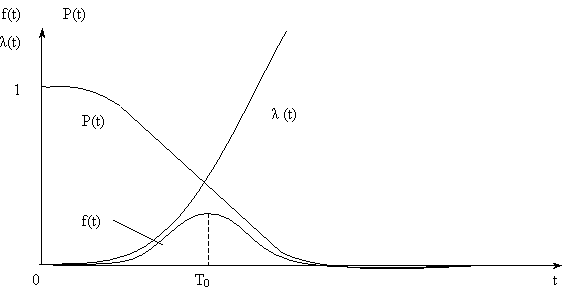
где Графики изменения показателей безотказности при нормальном распределении приведены на рис. 2. Выясним смысл параметров Т0 и S нормального распределения. Из графика f(t) видно, чтоТ0 является центром симметрии распределения, поскольку при изменении знака разности (t - T0) выражение (1) не меняется. При t = Т0 ПРО достигает своего максимума
Рис. 2
При сдвиге Т0 влево/вправо по оси абсцисс, кривая f(t) смещается в ту же сторону, не изменяя своей формы. Таким образом, Т0 является центром рассеивания случайной величины T, т. е. МО. Параметр S характеризует форму кривой f(t), т. е. рассеивание случайной величины T. Кривая ПРО f(t) тем выше и острее, чем меньше S. Изменение графиков P(t) и
Рис. 2
Используя полученные ранее соотношения между показателями надежности, можно было бы записать выражения для P(t); Q(t) и
распределенной нормально с параметрами, соответственно, МО и СКО M{X} = 0 и S{X}=1 и плотностью распределения
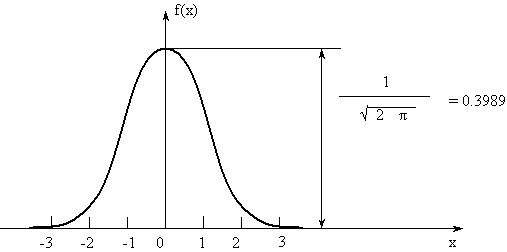
Выражение описывает плотность так называемого нормированного нормального распределения (рис. 3).
Рис. 3
Функция распределения случайной величины X запишется
а из симметрии кривой f(x) относительно МО M{X} = 0, следует, что f(-x) = f(x), откуда F(-x) = 1 - F(x). В справочной литературе приведены расчетные значения функций f(x) и F(x) для различных x = (t - Т0)/S. Показатели безотказности объекта через табличные значения f(x) и F(x) определяются по выражениям:
В практических расчетах часто вместо функции F(x) пользуются функцией Лапласа, представляющей распределение положительных значений случайной величины X в виде:
В литературе могут встретиться и другие выражения для Показатели надежности объекта можно определить через
Чаще всего при оценке надежности объекта приходится решать прямую задачу – при заданных параметрах Т0 и S нормально распределенной наработки до отказа определяется тот или иной показатель безотказности (например, ВБР) к интересующему значению наработки t. Но в ходе проектных работ приходится решать и обратную задачу – определение наработки, требуемой по техническому заданию, ВБР объекта. Для решения подобных задач используют квантили нормированного нормального распределения. Квантиль – значение случайной величины, соответствующее заданной вероятности. Обозначим: tp– значение наработки, соответствующее ВБР P; xp – значение случайной величины X, соответствующее вероятности P. Тогда из уравнения связи x и t:
при x = xp; t = tp, получаем tp= Т0 + xp S. tp, xp – ненормированные и нормированные квантили нормального распределения, соответствующие вероятности P. Значения квантилей xp приводятся в справочной литературе для P При заданной вероятности P < 0,5 используется соотношение
xp = - x1-p. Например, при P = 0,3 x0,3 = - x1- 0,3 = - x0, 7
2. Экспоненциальное распределение Экспоненциальное распределение описывает наработку до отказа объектов, у которых в результате сдаточных испытаний отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации. Эти объекты можно отнести к «не стареющим», поскольку они работают только на участке с f(t) = где 2. Логарифмически нормальное (логнормальное) распределение При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины T, а не сама эта величина. Логарифмически нормальное распределение во многом более точно, чем нормальное описывает наработку до отказа тех объектов, у которых отказ возникает вследствие усталости, например, подшипников качения, электронных ламп и пр. Если величина lg t имеет нормальное распределение с параметрами: МО U и СКО V, то величина T считается логарифмически нормально распределенной с ПРО, описываемой:
Параметры U и V по результатам испытаний принимаются:
где Показатели надежности можно рассчитать по приведенным в лекции 6 выражениям, пользуясь табулированными функциями f(x) и, соответственно, F(x) и
Рис. 4
3. Гамма–распределение Случайная величина наработки до отказа T имеет гамма-распределение с параметрами
где Г( Графики изменения показателей надежности при гамма-распределении приведены на рис. 5.
Рис. 5
Кроме рассмотренных законов распределения, в качестве моделей надежности объектов могут использоваться и другие, например: распределение Вейбулла, хорошо описывающее наработку объектов до отказа по усталостным разрушениям, распределение Релея, распределение Эрланга и т. п.
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 153; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.122.95 (0.011 с.) |

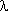 (t). Основной путь для получения модели состоит в проведении испытаний, вычислении статистических оценок и их аппроксимации аналитическими функциями.
(t). Основной путь для получения модели состоит в проведении испытаний, вычислении статистических оценок и их аппроксимации аналитическими функциями.
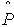 (t),
(t), 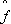 (t),
(t), 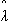 (t).
(t).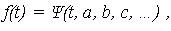
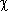 2 (хи-квадрат) Пирсона. Проверка согласованности распределений по критерию
2 (хи-квадрат) Пирсона. Проверка согласованности распределений по критерию 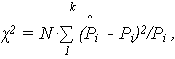
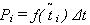 – теоретическая частота (вероятность) попадания случайной величины в интервал [ ti, ti +
– теоретическая частота (вероятность) попадания случайной величины в интервал [ ti, ti + 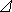 t ];
t ];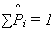 ;
;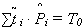 ;
;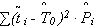 = D и т. д.
= D и т. д.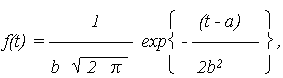

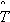 0,
0, 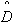 - оценки средней наработки и дисперсии.
- оценки средней наработки и дисперсии.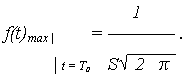
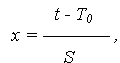
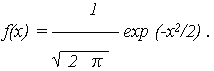
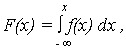
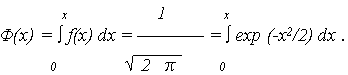
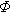 (x), поэтому, какой записью
(x), поэтому, какой записью 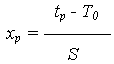
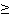 0,5.
0,5.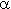 exp(-
exp(- 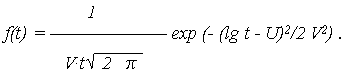
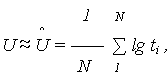
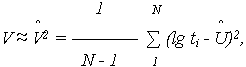
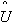 и
и  - оценки параметров U и V.
- оценки параметров U и V.
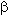 (параметр формы), где
(параметр формы), где