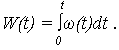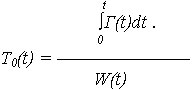Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы расчета надежности восстанавливаемых объектовСодержание книги
Поиск на нашем сайте
При расчете показателей надежности восстанавливаемых объектов и систем наиболее распространено допущение: экспоненциальное распределение наработки между отказами, экспоненциальное распределение времени восстановления. Применение экспоненциального распределения для описания процесса восстановления позволяет при ординарных независимых отказах представить анализируемые системы в виде марковских систем. При экспоненциальном распределении наработки между отказами и времени восстановления, для расчета надежности используют метод дифференциальных уравнений для вероятностей состояний (уравнений Колмогорова-Чепмена). Случайный процесс в какой либо физической системе S, называется марковским, если он обладает следующим свойством: для любого момента t0 вероятность состояния системы в будущем (t > t0) зависит только от состояния в настоящем (t = t0) и не зависит от того, когда и каким образом система пришла в это состояние (иначе: при фиксированном настоящем будущее не зависит от предыстории процесса - прошлого). Для марковского процесса «будущее» зависит от «прошлого» только через «настоящее», т. е. будущее протекание процесса зависит только от тех прошедших событий, которые повлияли на состояние процесса в настоящий момент. Марковский процесс, как процесс без последействия, не означает полной независимости от прошлого, поскольку оно проявляется в настоящем. При использовании метода, в общем случае, для системы S, необходимо иметь математическую модель в виде множества состояний системы S1 , S2 , …, Sn , в которых она может находиться при отказах и восстановлениях элементов. Для рассмотрения принципа составления модели введены допущения: - отказавшие элементы системы (или сам рассматриваемый объект) немедленно восстанавливаются (начало восстановления совпадает с моментом отказа); - отсутствуют ограничения на число восстановлений; - если все потоки событий, переводящих систему (объект) из состояния в состояние, являются пуассоновскими (простейшими), то случайный процесс переходов будет марковским процессом с непрерывным временем и дискретными состояниями S1 , S2 , …, Sn . Основные правила составления модели: 1. Математическую модель изображают в виде графа состояний. Элементы графа:
а) кружки (вершины графа S1 , S2 , …, Sn) – возможные состояния системы S, возникающие при отказах элементов; б) стрелки – возможные направления переходов из одного состояния Si в другое Sj.Над/под стрелками указываются интенсивности переходов.
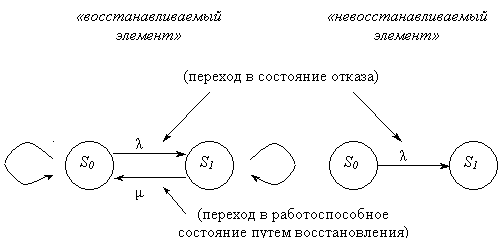
Рис.9. Примеры графа
На схеме оьозначены: S0 – работоспособное состояние; S1 – состояние отказа. «Петлей» обозначаются задержки в том или ином состоянии S0 и S1 соответствующие: исправное состояние продолжается; состояние отказа продолжается (в дальнейшем петли на графах не рассматриваем). Граф состояний отражает конечное (дискретное) число возможных состояний системы S1, S2 , …, Sn. Каждая из вершин графа соответствует одному из состояний. 2. Для описания случайного процесса перехода состояний (отказ/ восстановление) применяют вероятности состояний
P1(t), P2(t), …, Pi(t), …, Pn(t),
где Pi(t) – вероятность нахождения системы в момент t в i-м состоянии, т. е.
Pi(t) = P{S(t) = si}.
Очевидно, что для любого t
(нормировочное условие, поскольку иных состояний, кроме S1 , S2 , …, Sn нет). 3. По графу состояний составляется система обыкновенных дифференциальных уравнений первого порядка (уравнений Колмогорова-Чепмена При составлении дифференциальных уравнений пользуются простым мнемоническим правилом: а) в левой части – производная по времени t от Pi(t); б) число членов в правой части равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями; в) каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка; г) знак произведения положителен, если стрелка входит (направлена острием) в рассматриваемое состояние, и отрицателен, если стрелка выходит из него. Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений. 4. Чтобы решить систему дифференциальных уравнений для вероятностей состояний P1(t), Pi(t), …, Pn(t) необходимо задать начальное значение вероятностей P1(0), Pi(0), …, Pn(0), при t = 0, сумма которых равна единице:
Если в начальный момент t = 0 состояние системы известно, например, S(t=0) = Si, то Pi(0) = 1, а остальные равны нулю.
2. Показатели надежности восстанавливаемых систем. Все состояния системы S можно разделить на подмножества: SK SM S = SK SK 1. Функция готовности Г(t) системы определяет вероятность нахождения системы в работоспособном состоянии в момент t
где Pj(t) – вероятность нахождения системы в работоспособном j-м состоянии; Pz(t) – вероятность нахождения системы в неработоспособном z-м состоянии. 2. Функция простоя П(t) системы
3. Коэффициент готовности kг.с. системы определяется при установившемся режиме эксплуатации (при t
Коэффициент готовности kг.с. можно рассчитать по системе (2) дифференциальных уравнений, приравнивая нулю их левые части dPi(t)/dt = 0, т.к. Pi = const при t
и коэффициент готовности:
есть предельное значение функции готовности при установившемся режиме t
где 5. Функция потока отказов
6. Средняя наработка между отказами на интервале t
|
||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.175 (0.007 с.) |

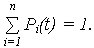
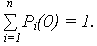
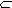 S – подмножество состояний j =
S – подмножество состояний j = 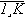 , в которых система работоспособна;
, в которых система работоспособна;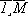 , в которых система неработоспособна.
, в которых система неработоспособна. SM,
SM,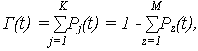
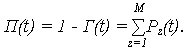

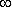 ). При t
). При t 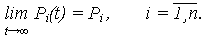
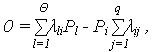
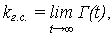
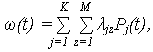
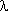 jz – интенсивности (обобщенное обозначение) переходов из работоспособного состояния в неработоспособное.
jz – интенсивности (обобщенное обозначение) переходов из работоспособного состояния в неработоспособное.