
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Институт сферы обслуживания и предпринимательства (филиал)Содержание книги
Поиск на нашем сайте
Институт сферы обслуживания и предпринимательства (филиал) федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Донской государственный технический университет» В г. Шахты Ростовской области (ИСО и П (филиал) ДГТУ)
Утверждаю Заведующий кафедрой «СиТБ» _____________С.А. Масленников «05» сентября 2014г.
На правах рукописи
М.Д. Молев НАДЁЖНОСТЬ ТЕХНИЧЕСКИХ СИСТЕМ И ТЕХНОГЕННЫЙРИСК Конспект лекций
Рассмотрен и рекомендован для использования в учебном процессе на 2014/2015 – 2017/2018 учебные годы на заседании кафедры «СиТБ». Протокол № 2 от 05.09.2014 г.
ШАХТЫ 2014 ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ НАДЁЖНОСТИ
Основные вопросы, которые изучает теория надёжности: отказы технических элементов (средств, систем); критерии и количественные характеристики надёжности; методы анализа и повышения надёжности элементов и систем на этапах проектирования, изготовления и эксплуатации; методы испытания технических средств на надёжность; методы оценки эффективности и повышения надёжности. Надёжность – это свойство объекта выполнять заданные функции, сохраняя во времени и в заданных пределах значения установленных эксплуатационных показателей.
Показатели надёжности В теории надежности используют понятия объект, элемент, система. Дадим их определения. Объект – техническое изделие определенного целевого назначения, рассматриваемое в периоды проектирования, производства, испытаний и эксплуатации. Объектами могут быть различные системы и их элементы. Элемент – простейшая составная часть изделия, в задачах надежности может состоять из многих деталей. Система – совокупность совместно действующих элементов, предназначенная для самостоятельного выполнения заданных функций. Понятия элемента и системы трансформируются в зависимости от поставленной задачи. Например, станок, при установлении его собственной надёжности рассматривается как система, состоящая из отдельных элементов – механизмов и деталей, а при изучении надёжности технологической линии – как элемент. Надёжность объекта характеризуется следующими основными состояниями и событиями. Исправность – состояние объекта, при котором он соответствует всем требованиям, установленным нормативно-технической документацией (НТД). Работоспособность – состояние объекта, при котором он способен выполнять заданные функции, сохраняя значения основных параметров, установленных НТД. Основные параметры характеризуют функционирование объекта при выполнении поставленных задач. Понятие исправность шире, чем понятие работоспособность. Работоспособный объект обязан удовлетворять лишь тем требования НТД, выполнение которых обеспечивает нормальное применение объекта по назначению. Таким образом, если объект неработоспособен, то это свидетельствует о его неисправности. С другой стороны, если объект неисправен, то это не означает, что он неработоспособен. Предельное состояние – состояние объекта, при котором его применение по назначению недопустимо или нецелесообразно. Применение (использование) объекта по назначению прекращается в следующих случаях: при неустранимом нарушении безопасности, при неустранимом отклонении величин заданных параметров, при недопустимом увеличении эксплуатационных расходов. Для некоторых объектов предельное состояние является последним в его функционировании, для других – определенной фазой в эксплуатационном графике, требующей проведения ремонтно-восстановительных работ. В связи с этим, объекты могут быть: невосстанавливаемые, для которых работоспособность в случае возникновения отказа, не подлежит восстановлению; восстанавливаемые, работоспособность которых может быть восстановлена, в том числе и путем замены. Отказ – событие, заключающееся в нарушении работоспособного состояния объекта. Критерий отказа – отличительный признак или совокупность признаков, согласно которым устанавливается факт возникновения отказа. Надёжность является комплексным свойством, включающим в себя в зависимости от назначения объекта или условий его эксплуатации ряд простых свойств: безотказность, долговечность, ремонтопригодность, сохраняемость. Безотказность – свойство объекта непрерывно сохранять работоспособность в течение некоторой наработки или в течение некоторого времени. Наработка – продолжительность или объём работы объекта, измеряемая в любых неубывающих величинах (единица времени, число циклов нагружения, километры пробега и т. п.). Долговечность – свойство объекта сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонтов. Ремонтопригодность – свойство объекта, заключающееся в его приспособленности к предупреждению и обнаружению причин возникновения отказов, поддержанию и восстановлению работоспособности путем проведения ремонтов и технического обслуживания. Сохраняемость – свойство объекта непрерывно сохранять требуемые эксплуатационные показатели в течение (и после) срока хранения и транспортирования. В зависимости от объекта надёжность может определяться всеми перечисленными свойствами или частью их. Например, надёжность колеса зубчатой передачи, подшипников определяется их долговечностью, а станка – долговечностью, безотказностью и ремонтопригодностью. Показатель надёжности количественно характеризует, в какой степени данному объекту присущи определённые свойства, обусловливающие надёжность. Одни показатели надёжности имеют размерность, ряд других являются безразмерными. Технический ресурс – наработка объекта от начала его эксплуатации или возобновления эксплуатации после ремонта до наступления предельного состояния. Строго говоря, технический ресурс может быть регламентирован следующим образом: до среднего, капитального, от капитального до ближайшего среднего ремонта и т. п. Если регламентация отсутствует, то имеется в виду ресурс от начала эксплуатации до достижения предельного состояния после всех видов ремонтов. Для невосстанавливаемых объектов понятия технического ресурса и наработки до отказа совпадают. Назначенный ресурс – суммарная наработка объекта, при достижении которой эксплуатация должна быть прекращена независимо от его состояния. Срок службы –календарная продолжительность эксплуатации (в том числе, хранение, ремонт и т. п.) от ее начала до наступления предельного состояния. Наработка до отказа – вероятность того, что в пределах заданной наработки отказ объекта не возникнет (при условии работоспособности в начальный момент времени). Средняя наработка до отказа – математическое ожидание случайной наработки объекта до первого отказа. Средняя наработка между отказами – математическое ожидание случайной наработки объекта между отказами. Средняя наработка на отказ – отношение наработки восстанавливаемого объекта за некоторый период времени к математическому ожиданию числа отказов в течение этой наработки. Этим термином можно назвать кратко среднюю наработку до отказа и среднюю наработку между отказами, когда оба показателя совпадают. Для совпадения последних необходимо, чтобы после каждого отказа объект восстанавливался до первоначального состояния. Среднее время простоя – математическое ожидание случайного времени вынужденного нерегламентированного пребывания объекта в состоянии неработоспособности. Среднее время восстановления – математическое ожидание случайной продолжительности восстановления работоспособности (собственно ремонта). Средний коэффициент готовности – усредненное на заданном интервале времени значение нестационарного коэффициента готовности. Стационарный коэффициент готовности (коэффициент готовности) – вероятность того, что восстанавливаемый объект окажется работоспособным в произвольно выбранный момент времени в установившемся процессе эксплуатации. Коэффициент готовности может быть определен и как отношение времени, в течение которого объект находится в работоспособном состоянии, к общей длительности рассматриваемого периода. Предполагается, что рассматривается установившийся процесс эксплуатации, математической моделью которого является стационарный случайный процесс. Коэффициент готовности является предельным значением, к которому стремятся и нестационарный, и средний коэффициенты готовности с ростом рассматриваемого интервала времени. Интенсивность отказов – условная плотность вероятности отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник. Параметр потока отказов – плотность вероятности возникновения отказа восстанавливаемого объекта, определяемая для рассматриваемого момента времени. Параметр потока отказа может быть определен как отношение числа отказов объекта за определенный интервал времени к длительности этого интервала при ординарном потоке отказов.
Выбор закона распределения Выбор закона распределения состоит в подборе аналитической функции наилучшим образом аппроксимирующей эмпирические функции надежности. Выбор, в значительной мере, процедура неопределенная и во многом субъективная, при этом многое зависит от априорных знаний об объекте и его свойствах, условиях работы, а также анализа вида графиков Очевидно, что выбор распределения будет зависеть, прежде всего, от вида эмпирической функции ПРО Предположим, что по тем или иным соображениям, выбран гипотетический закон распределения, заданный теоретической ПРО
где a, b, c, … - неизвестные параметры распределения. Требуется подобрать эти параметры так, чтобы функция f(t) наилучшим образом сглаживала ступенчатый график На графике вместе с Расчет критерия согласия Критерий согласия – это критерий проверки гипотезы о том, что случайная величина T, представленная своей выборкой, имеет распределение предполагаемого типа. Проверка состоит в следующем. Рассчитывается критерий, как некоторая мера расхождения теоретического и эмпирического распределений, причем эта мера является случайной величиной. Чем больше мера расхождения, тем хуже согласованность эмпирического распределения с теоретическим, т. е. меньше мала, то гипотезу о выборе закона распределения следует отвергнуть, как мало правдоподобную. В противном случае – экспериментальные данные не противоречат принятому распределению. Из известных критериев наиболее применяемый критерий согласия - рассчитывается критерий
где - определяется число степеней свободы R = k – L, где L – число независимых условий, наложенных на частоты а) условие б) условие совпадения в) условие совпадения Чаще всего L = 3. Чем больше число степеней свободы, тем больше случайная величина - по рассчитанным Ответ на вопрос: насколько мала должна быть вероятность P, чтобы отбросить гипотезу о выборе того или иного закона распределения – во многом неопределенный. На практике, если P < 0,1, то рекомендуется подыскать другой закон распределения. В целом, с помощью критерия согласия, можно опровергнуть выбранную гипотезу, если же P достаточно велика, то это не может служить доказательством правильности гипотезы, а указывает лишь на то, что гипотеза не противоречит данным эксперимента. 1. Классическое нормальное распределение Нормальное распределение или распределение Гаусса является наиболее универсальным, удобным и широко применяемым. Считается, что наработка подчинена нормальному распределению (нормально распределена), если плотность распределения отказов (ПРО) описывается выражением:
где a и b – параметры распределения, соответственно, МО и СКО, которые по результатам испытаний принимаются:
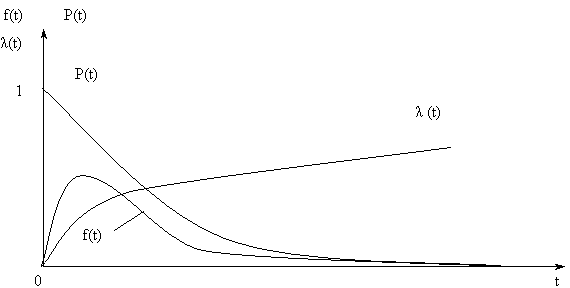
где Графики изменения показателей безотказности при нормальном распределении приведены на рис. 2. Выясним смысл параметров Т0 и S нормального распределения. Из графика f(t) видно, чтоТ0 является центром симметрии распределения, поскольку при изменении знака разности (t - T0) выражение (1) не меняется. При t = Т0 ПРО достигает своего максимума
Рис. 2
При сдвиге Т0 влево/вправо по оси абсцисс, кривая f(t) смещается в ту же сторону, не изменяя своей формы. Таким образом, Т0 является центром рассеивания случайной величины T, т. е. МО. Параметр S характеризует форму кривой f(t), т. е. рассеивание случайной величины T. Кривая ПРО f(t) тем выше и острее, чем меньше S. Изменение графиков P(t) и
Рис. 2
Используя полученные ранее соотношения между показателями надежности, можно было бы записать выражения для P(t); Q(t) и
распределенной нормально с параметрами, соответственно, МО и СКО M{X} = 0 и S{X}=1 и плотностью распределения
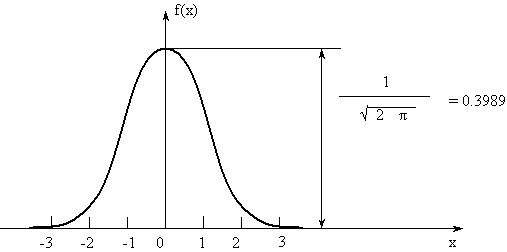
Выражение описывает плотность так называемого нормированного нормального распределения (рис. 3).
Рис. 3
Функция распределения случайной величины X запишется
а из симметрии кривой f(x) относительно МО M{X} = 0, следует, что f(-x) = f(x), откуда F(-x) = 1 - F(x). В справочной литературе приведены расчетные значения функций f(x) и F(x) для различных x = (t - Т0)/S. Показатели безотказности объекта через табличные значения f(x) и F(x) определяются по выражениям:
В практических расчетах часто вместо функции F(x) пользуются функцией Лапласа, представляющей распределение положительных значений случайной величины X в виде:
В литературе могут встретиться и другие выражения для Показатели надежности объекта можно определить через
Чаще всего при оценке надежности объекта приходится решать прямую задачу – при заданных параметрах Т0 и S нормально распределенной наработки до отказа определяется тот или иной показатель безотказности (например, ВБР) к интересующему значению наработки t. Но в ходе проектных работ приходится решать и обратную задачу – определение наработки, требуемой по техническому заданию, ВБР объекта. Для решения подобных задач используют квантили нормированного нормального распределения. Квантиль – значение случайной величины, соответствующее заданной вероятности. Обозначим: tp– значение наработки, соответствующее ВБР P; xp – значение случайной величины X, соответствующее вероятности P. Тогда из уравнения связи x и t:
при x = xp; t = tp, получаем tp= Т0 + xp S. tp, xp – ненормированные и нормированные квантили нормального распределения, соответствующие вероятности P. Значения квантилей xp приводятся в справочной литературе для P При заданной вероятности P < 0,5 используется соотношение
xp = - x1-p. Например, при P = 0,3 x0,3 = - x1- 0,3 = - x0, 7
2. Экспоненциальное распределение Экспоненциальное распределение описывает наработку до отказа объектов, у которых в результате сдаточных испытаний отсутствует период приработки, а назначенный ресурс установлен до окончания периода нормальной эксплуатации. Эти объекты можно отнести к «не стареющим», поскольку они работают только на участке с f(t) = где 2. Логарифмически нормальное (логнормальное) распределение При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины T, а не сама эта величина. Логарифмически нормальное распределение во многом более точно, чем нормальное описывает наработку до отказа тех объектов, у которых отказ возникает вследствие усталости, например, подшипников качения, электронных ламп и пр. Если величина lg t имеет нормальное распределение с параметрами: МО U и СКО V, то величина T считается логарифмически нормально распределенной с ПРО, описываемой:
Параметры U и V по результатам испытаний принимаются:
где Показатели надежности можно рассчитать по приведенным в лекции 6 выражениям, пользуясь табулированными функциями f(x) и, соответственно, F(x) и
Рис. 4
3. Гамма–распределение Случайная величина наработки до отказа T имеет гамма-распределение с параметрами
где Г( Графики изменения показателей надежности при гамма-распределении приведены на рис. 5.
Рис. 5
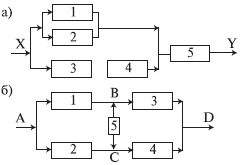
Кроме рассмотренных законов распределения, в качестве моделей надежности объектов могут использоваться и другие, например: распределение Вейбулла, хорошо описывающее наработку объектов до отказа по усталостным разрушениям, распределение Релея, распределение Эрланга и т. п. Объектов Расчеты надежности – расчеты, предназначенные для определения количественных показателей надежности. Они проводятся на различных этапах разработки, создания и эксплуатации объектов. Элементный расчет – определение показателей надежности объекта, обусловленных надежностью его комплектующих частей (элементов). В результате такого расчета оценивается техническое состояние объекта (вероятность того, что объект будет находиться в работоспособном состоянии, средняя наработка на отказ и т. п.). Одним из способов расчета является расчет с использованием блок-схем (структурных схем). Под структурной схемой надежности понимается наглядное представление (графическое или в виде логических выражений) условий, при которых работает или не работает исследуемый объект (система, устройство, технический комплекс и т.д.). Типовые структурные схемы представлены на рис. 6.
Рис. 6. Типовые структуры расчета надежности Простейшей формой структурной схемы надежности является параллельно-последова-тельная структура. На ней параллельно соединяются элементы, совместный отказ которых приводит к отказу системы. В последовательную цепочку соединяются такие элементы, отказ любого из которых приводит к отказу объекта. На рис. 6,а представлен вариант параллельно-последовательной структуры. По этой структуре можно сделать следующее заключение. Объект состоит из пяти частей. Отказ объекта наступает тогда, когда откажет или элемент 5, или узел, состоящий из элементов 1-4. Узел может отказать тогда, когда одновременно откажет цепочка, состоящая из элементов 3,4 и узел, состоящий из элементов 1,2. Цепь 3-4 отказывает, если откажет хотя бы один из составляющих ее элементов, а узел 1,2 - если откажут оба элемента, т.е. элементы 1,2. Расчет надежности при наличии таких структур отличается наибольшей простотой и наглядностью. Однако не всегда удается условие работоспособности представить в виде простой параллельно-последователь-ной структуры. В таких случаях используют или логические функции, или графы и ветвящиеся структуры, по которым оставляются системы уравнений работоспособности. На основе структурной схемы надежности составляется набор расчетных формул. Для типовых случаев расчета используются формулы, приведенные в справочниках по расчетам надежности, стандартах и методических указаниях. Самым простым случаем в расчетном смысле является последовательное соединение элементов системы. В такой системе отказ любого элемента равносилен отказу системы в целом. По аналогии с цепочкой последовательно соединенных проводников, обрыв каждого из которых равносилен размыканию всей цепи, мы и называем такое соединение "последовательным" (рис. 7). Следует пояснить, что "последовательным" такое соединение элементов является только в смысле надежности, физически они могут быть соединены как угодно.
Рис. 7. Блок-схема системы с последовательным соединением элементов С позиции надежности, такое соединение означает, что отказ устройства, состоящего из этих элементов, происходит при отказе элемента 1 или элемента 2, или элемента 3, или элемента n. Условие работоспособности можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1 и элемент 2, и элемент 3, и элемент n. Выразим надежность данной системы через надежности ее элементов. Пусть имеется некоторый промежуток времени (0, t), в течение которого требуется обеспечить безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности Р(t), нам важно знать значение этой надежности при t=t, т.е. Р(t). Это не функция, а определенное число; отбросим аргумент t и обозначим надежность системы просто Р. Аналогично обозначим надежности отдельных элементов P1, P2, P3,..., Pn. Для безотказной работы простой системы в течение времени t нужно, чтобы безотказно работал каждый из ее элементов. Обозначим S - событие, состоящее в безотказной работе системы за время t; s1, s2, s3,..., sn - события, состоящие в безотказной работе соответствующих элементов. Событие S есть произведение (совмещение) событий s1, s2, s3,..., sn: а короче P = т.е. надежность (вероятность работоспособного состояния) простой системы, составленной из независимых по отказам, последовательно соединенных элементов, равна произведению надежностей ее элементов. На рис. 4.5.6 представлено параллельное соединение элементов 1, 2, 3. Это означает, что устройство, состоящее из этих элементов, переходит в состояние отказа после отказа всех элементов при условии, что все элементы системы находятся под нагрузкой, а отказы элементов статистически независимы.
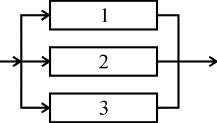
Рис. 8. Блок-схема системы с параллельным соединением элементов Условие работоспособности устройства можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1 или элемент 2, или элемент 3, или элементы 1 и 2, 1; и 3, 2; и 3, 1; и 2; и 3. Вероятность безотказного состояния устройства, состоящего из n параллельно соединенных элементов определяется по теореме сложения вероятностей совместных случайных событий как Для приведенной блок-схемы, состоящей из трех элементов, выражение (4.5.7) можно за писать:
ТЕХНОГЕННЫЙ РИСК 2.1. Понятие техногенного риска При решении вопросов безопасности жизнедеятельности населения применяется теория риска, основу которой составляет определение последствий и вероятности нежелательных событии. Используя количественные показатели риска, в принципе можно «измерять» потенциальную опасность и даже сравнивать опасности различной природы. При этом в качестве показателей опасности обычно понимается индивидуальный риск гибели людей (или. в общем случае, причинения определенного ущерба). В широком смысле слова риск выражает возможную опасность, вероятность нежелательного события. Применительно к проблеме безопасности жизнедеятельности таким событием может быть ухудшение здоровья или смерть человека, авария или катастрофа технической системы или устройства, загрязнение экологических систем, гибель людей или возрастание смертности населения, материальных ущерб от реализовавшихся опасностей или увеличения затрат на безопасность. Общим во всех приведенных представлениях является то, что риск включает неуверенность – произойдет ли нежелательное событие и возникнет ли неблагоприятное состояние. В соответствии с современными научными взглядами риск интерпретируется как вероятностная мера возникновения техногенных или природных явлений, сопровождающихся возникновением, формированием и действием опасностей и нанесенного при этом социального, экономического, экологического и других видов ущерба и вреда. Таким образом, под риском следует понимать ожидаемую частоту или вероятность возникновения опасностей определенного класса или размер возможного ущерба от нежелательного события или комбинацию данных величин. Аналитически риск выражает частоту реализации опасностей по отношению к их числу
где R - риск; N - количественный показатель частоты нежелательных событий в единицу времени t; Q - число объектов риска, подверженных определенному фактору риска Ожидаемый (прогнозируемый) риск R - это произведение частоты реализации конкретной опасности на произведение вероятностей нахождения человека в «зоне риска» при различном регламенте технологического процесса:
Величина риска определяется как произведение величины нежелательного события на вероятность его наступления, т. е. как математическое ожидание величины нежелательных последствий. Отображение множества исходных причин развития риска можно в общем виде записать формулу расчета в виде:
где: R – риск, т. е. вероятность нанесения определенного ущерба; P1 – вероятность возникновения события или явления, обусловливающего формирование и действие опасных факторов; P2 – вероятность формирования определенных уровней физических полей, ударных нагрузок, полей концентрации вредных веществ, воздействующих на людей и другие объекты; P3 – вероятность того, что указанные уровни полей и нагрузок приведут к определенному ущерб P4 – вероятность отказа средств защиты.
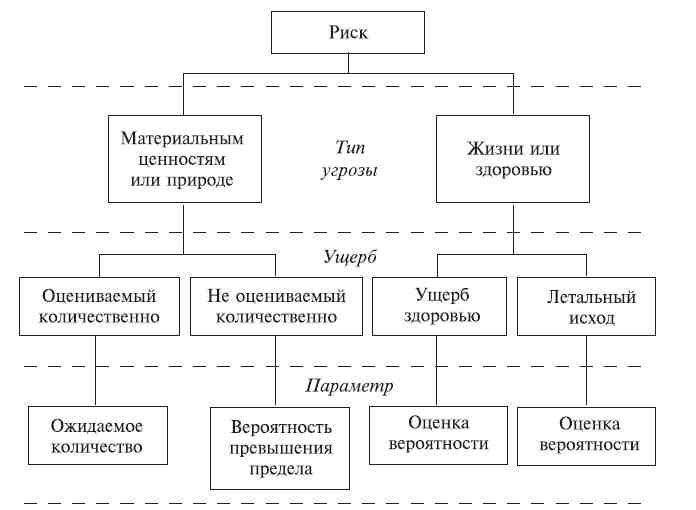
Виды риска
Рисунок 11. Виды риска и возможности его оценки
Соотношение объектов риска и нежелательных событий позволяет различать индивидуальный, технический (техногенный), экологический, социальный и экономический риски.Техногенный риск – это комплексный показатель надежности элементов техносферы, выражающий вероятность аварии (катастрофы) при эксплуатации производственного оборудования и реализации технологических процессов:
где Rт – техногенный риск, АT – число аварий в единицу времени t на объектах; Т – число идентичных объектов, подверженных общему фактору риска. Наиболее распространенные факторы техногенного риска: ошибочный выбор по критериям безопасности направлений развития техники и технологий; выбор потенциально опасных конструктивных схем и принципов действия
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 78; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.191 (0.011 с.) |

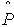 (t),
(t), 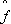 (t),
(t), 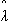 (t).
(t).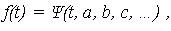
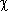 2 (хи-квадрат) Пирсона. Проверка согласованности распределений по критерию
2 (хи-квадрат) Пирсона. Проверка согласованности распределений по критерию 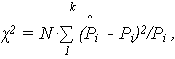
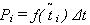 – теоретическая частота (вероятность) попадания случайной величины в интервал [ ti, ti +
– теоретическая частота (вероятность) попадания случайной величины в интервал [ ti, ti + 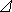 t ];
t ];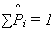 ;
;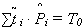 ;
;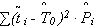 = D и т. д.
= D и т. д.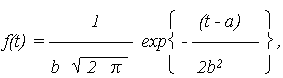

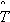 0,
0, 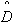 - оценки средней наработки и дисперсии.
- оценки средней наработки и дисперсии.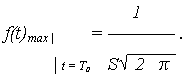
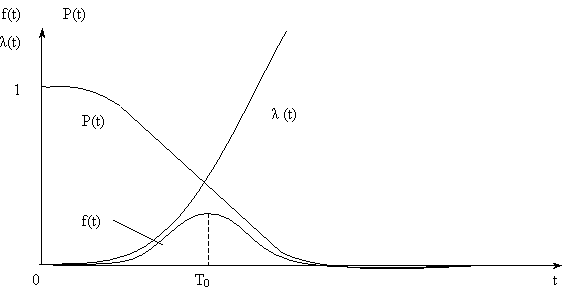
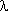 (t) при различных СКО наработок (S1 < S2 < S3) и Т0 = const приведено на рис. 3.
(t) при различных СКО наработок (S1 < S2 < S3) и Т0 = const приведено на рис. 3.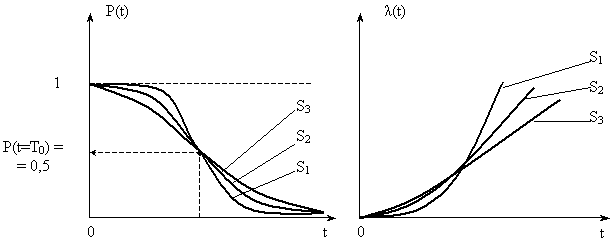
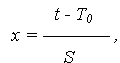
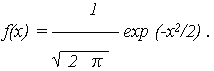
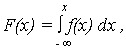
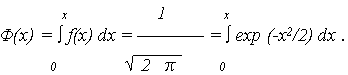
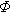 (x), поэтому, какой записью
(x), поэтому, какой записью 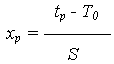
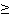 0,5.
0,5.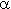 exp(-
exp(- 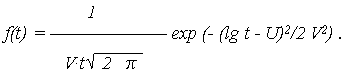
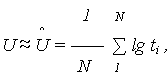
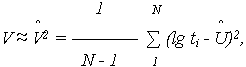
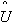 и
и  - оценки параметров U и V.
- оценки параметров U и V.
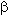 (параметр формы), где
(параметр формы), где 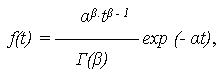

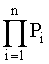 ,
, 
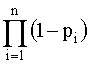 , (4.5.8)
, (4.5.8)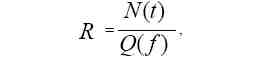
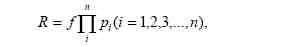
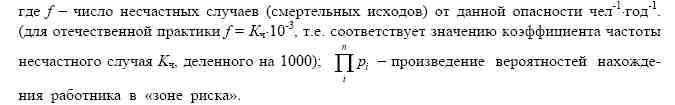
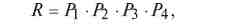
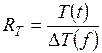 ;
;


