Расчет элементов стальных конструкций на осевые силы и изгиб.
ЦЕНТРАЛЬНО-РАСТЯНУТЫЕ И ЦЕНТРАЛЬНО-СЖАТЫЕ ЭЛЕМЕНТЫ.
5.1. Расчет на прочность элементов, подверженных центральному растяжению или сжатию силой N, кроме указанных в п. 5.2, следует выполнять по формуле
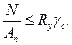 (5) (5)
Расчет на прочность сечений в местах крепления растянутых элементов из одиночных уголков, прикрепляемых одной полкой болтами, следует выполнять по формулам (5) и (6). При этом значение γс в формуле (6) должно приниматься по прил. 4 настоящих норм.
5.2. Расчет на прочность растянутых элементов конструкций из стали с отношением Ru /γ u > Rγ, эксплуатация которых возможна и после достижения металлом предела текучести, следует выполнять по формуле
N/An≤Ruγc / γu (6)
5.3. Расчет на устойчивость сплошностенчатых элементов, подверженных центральному сжатию силой N, следует выполнять по формуле
N/φA≤ Ryγc. (7)
ИЗГИБАЕМЫЕ ЭЛЕМЕНТЫ
5.12. Расчет на прочность элементов (кроме балок с гибкой стенкой, с перфорированной стенкой и подкрановых балок), изгибаемых в одной из главных плоскостей, следует выполнять по формуле
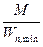 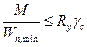 (28) (28)
Значения касательных напряжений τ в сечениях изгибаемых элементов должны удовлетворять условию
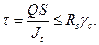 (29) (29)
При наличии ослабления стенки отверстиями для болтов значения τ в формуле (29) следует умножать на коэффициент α, определяемый по формуле
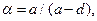 (30) (30)
где a – шаг отверстий; d – диаметр отверстия.
РАСЧЕТ ЛИСТОВЫХ КОНСТРУКЦИЙ
РАСЧЕТ НА ПРОЧНОСТЬ
8.1. Расчет на прочность листовых конструкций (оболочек вращения), находящихся в безмоментном напряженном состоянии, следует выполнять по формуле
 (93) (93)
где 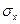 и и 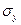 - нормальные напряжения по двум взаимно перпендикулярным направлениям; - нормальные напряжения по двум взаимно перпендикулярным направлениям;
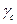 - коэффициент условий работы конструкций, назначаемый в соответствии с требованиямиСНиП по проектированию сооружений промышленных предприятий. При этом абсолютные значения главных напряжений должны быть не более значений расчетных сопротивлений, умноженных на ус. - коэффициент условий работы конструкций, назначаемый в соответствии с требованиямиСНиП по проектированию сооружений промышленных предприятий. При этом абсолютные значения главных напряжений должны быть не более значений расчетных сопротивлений, умноженных на ус.
8.2. Напряжения в безмоментных тонкостенных оболочках вращения (рис. 17), находящихся под давлением жидкости, газа или сыпучего материала, следует определять по формулам:
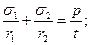 (94) (94)
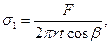 (95) (95)
где σ1 и σ2 — соответственно меридиональное и кольцевое напряжения; r1 и r2— радиусы кривизны в главных направлениях срединной поверхности оболочки;
р — расчетное давление на единицу поверхности оболочки;
t — толщина оболочки;
F — проекция на ось z - z оболочки полного расчетного давления, действующего на часть оболочки аЬс (рис. 17); и р — радиус и угол, показанные на рис. 17.
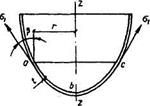
Рис.17. Схема оболочки вращения
8.3. Напряжения в замкнутых безмоментных тонкостенных оболочках вращения, находящихся под внутренним равномерным давлением, следует определять по формулам:
для цилиндрических оболочек
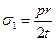 и и 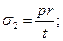 (96) (96)
для сферических оболочек
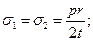 (97) (97)
для конических оболочек
 и и  (98) (98)
где p - расчетное внутреннее давление на единицу поверхности оболочки; r – радиус срединной поверхности оболочки (рис. 18);
β – угол между образующей конуса и его осью z – z (рис. 18).
Рис. 18. Схема конической оболочки вращения
8.4. В местах изменения формы или толщины оболочек, а также изменения нагрузки должны быть учтены местные напряжения (краевой эффект).
|