Какую точку плоской фигуры называют мгновенным центром скоростей (мцс)?
А. Точка, скорость которой в данное мгновение известна, называется мцс.
Б. Мцс-эта точка фигуры, находящейся в плоском движении, скорость которой равна сумме скорости полюса и вращательной скорости вокруг полюса.
В. Ту точку фигуры, совершающей плоское движение, скорость которой в данное мгновение равна нулю, называют мцс.
Г. В каждый момент времени при плоском движении фигуры в ее плоскости, если  , имеется единственная точка этой фигуры, скорость которой равна нулю. Эту точку называют мцс. , имеется единственная точка этой фигуры, скорость которой равна нулю. Эту точку называют мцс.
54. На каких рисунках (рис.19) положения мгновенного центра скоростей определены правильно?
А. Случай а) и д);
Б. Случай б);
В. Случай е);
Г. Случай в) и г).
Рис.19
55. Направления скоростей каких точек колеса указаны на рис.20 правильно?
Рис. 20
А. Точек 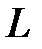 и М; Б. Точек N, Е; B. Точек В, D; Г. Точек О, К. и М; Б. Точек N, Е; B. Точек В, D; Г. Точек О, К.
56. Укажите, в каких случаях положения МЦС звена АВ указаны правильно (рис. 21).
Рис. 21
А. Случай б); Б. Случай а); В. Случай в); Г. Случай г).
57. Определить скорость точки В колеса, если точка А колеса имеет скорость 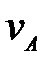 (рис. 22). (рис. 22).
Рис. 22
58. В каких случаях скорости точек А, В, С, D блока 2 определены правильно? 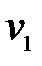 -скорость груза 1 (рис.23). -скорость груза 1 (рис.23).
Рис.23
59.
|
| Найти 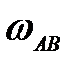 шатуна АВ, если в
данное мгновение известна скорость точки шатуна АВ, если в
данное мгновение известна скорость точки 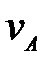 (рис.24). (рис.24).
| Рис. 24
А. 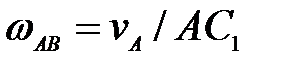 ; Б. ; Б. 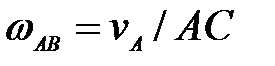 ; ;
В. 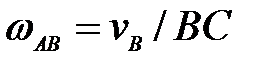 , , 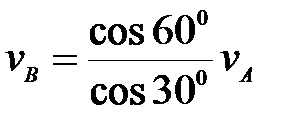 ; Г. ; Г. 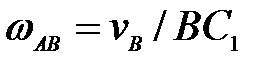 , , 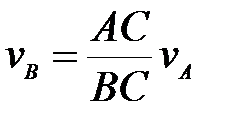 . .
60. Для данного положения механизма (рис. 25) определить
Рис.25
А. 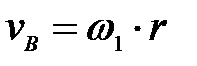 ; ; 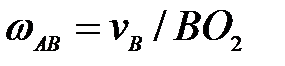 ; ;
Б. 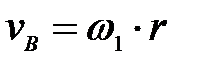 ; ; 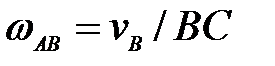 ; ;
В. 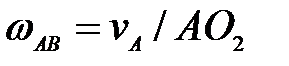 ; ; 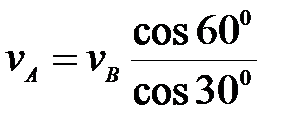 ; ;
Г. 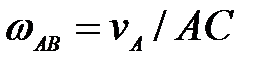 . .
61.
|
| Для данного положения
механизма (рис.26) определить угловую скорость шкива 2, если известна 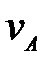 . .
| Рис. 26
А. 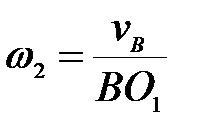 ; ; 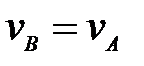 ; ; 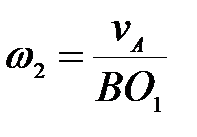 ; ;
Б. 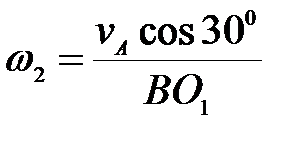 ; ;
В. 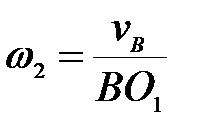 ; ; 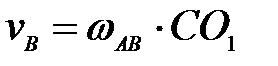 ; ; 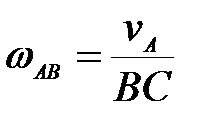 ; ; 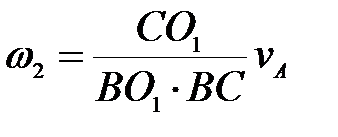 . .
Г. 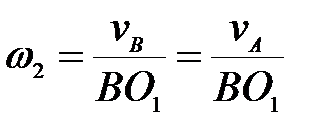 , т.к. , т.к. 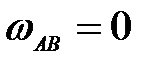 . .
УСКОРЕНИЯ ТОЧЕК ТЕЛА ПРИ ПЛОСКОМ ДВИЖЕНИИ
62. Как определяется ускорение любой точки плоской фигуры?
Рис. 27
А. Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и нормального ускорения этой точки во вращении вокруг полюса (рис. 27а), т.е. 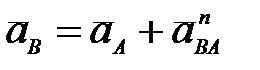 ; ;
Б. Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и касательного ускорения этой точки во вращении вокруг полюса (рис. 27б), т.е. 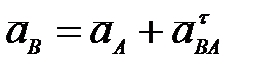 ; ;
В. Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и вращательного ускорения этой точки вокруг полюса (рис. 27в), т.е. 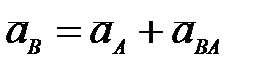 ; ;
Г. Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса, нормального и касательного ускорений этой точки во вращении вокруг полюса (рис. 27г), т.е. 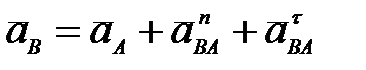 ; ;
63. Как определяется ускорение точки В плоской фигуры (рис. 28) в данный момент времени, если 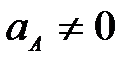 и и 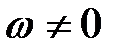 , , 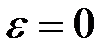 ? ?
Рис. 28
А. 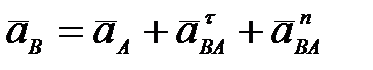 (рис. 28а)); (рис. 28а));
Б. 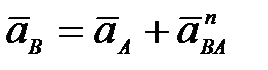 (рис. 28б)); (рис. 28б));
В. 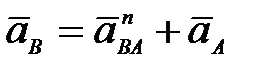 (рис. 28в)); (рис. 28в));
Г. 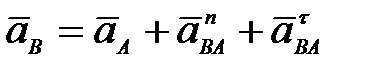 (рис. 28г)). (рис. 28г)).
64. Как определяется ускорение точки В плоской фигуры в данный момент времени, если 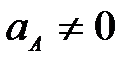 и и 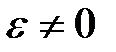 , , 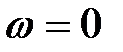 (рис. 29). (рис. 29).
Рис. 29
А. 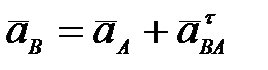 (рис. 29а)). (рис. 29а)).
Б. 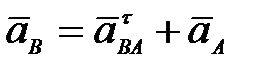 (рис. 29б)). (рис. 29б)).
В.  (рис. 29в)). (рис. 29в)).
Г. 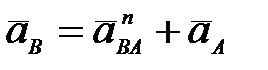 (рис. 29г)). (рис. 29г)).
65. Кривошип ОА вращается равномерно с угловой скоростью 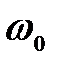 (рис.30). В каких случаях ускорение ползуна В определено верно? (рис.30). В каких случаях ускорение ползуна В определено верно?
Рис. 30
А. 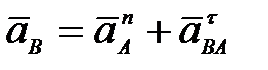 (рис. 30а). Б. (рис. 30а). Б. 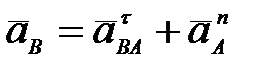 (рис. 30б). (рис. 30б).
В. 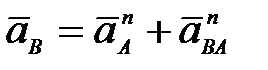 (рис. 30в). Г. (рис. 30в). Г. 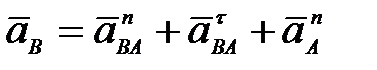 (рис. 30г). (рис. 30г).
66. Колесо радиуса R катиться без скольжения (рис. 31). Для каких случаев ускорение 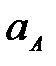 точки а определено правильно. точки а определено правильно.
Рис. 31
А. 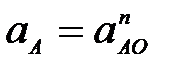 ; ; 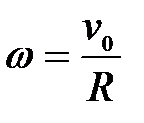 ; ; 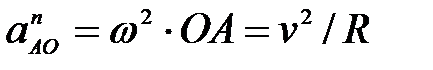 (рис. 31а). (рис. 31а).
Б. 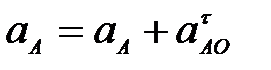 ; ; 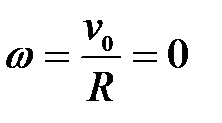 ; ; 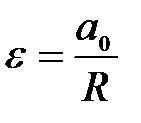 ; ; 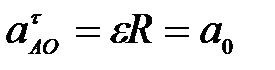 ; ; 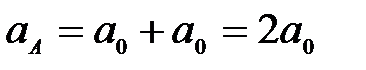 (рис. 31б); (рис. 31б);
В. 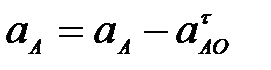 ; ; 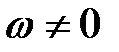 ; ; 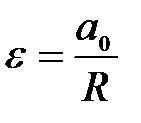 ; ; 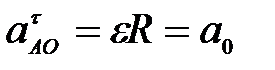 ; ; 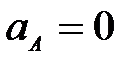 (рис. 31в)); (рис. 31в));
Г. 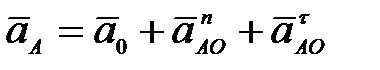 ; ; 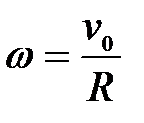 ; ; 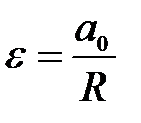 ; ; 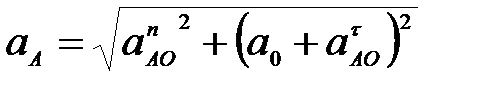 ; ; 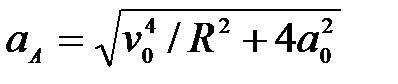 ; (рис. 31г)); ; (рис. 31г));
|


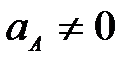 и
и 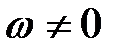 ,
, 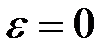 ?
?
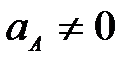 и
и 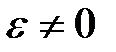 ,
, 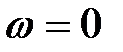 (рис. 29).
(рис. 29).
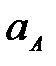 точки а определено правильно.
точки а определено правильно.

 , имеется единственная точка этой фигуры, скорость которой равна нулю. Эту точку называют мцс.
, имеется единственная точка этой фигуры, скорость которой равна нулю. Эту точку называют мцс.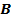
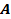


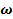
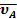
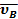
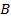
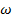
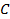
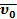
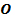
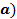
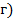
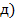
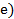
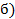
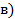

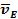
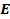
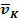
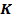
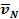
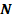
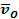
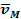
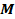
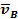
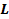
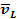
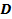

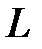 и М; Б. Точек N, Е; B. Точек В, D; Г. Точек О, К.
и М; Б. Точек N, Е; B. Точек В, D; Г. Точек О, К.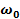
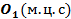
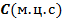
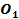
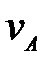 (рис. 22).
(рис. 22).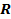
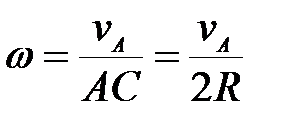 ;
; 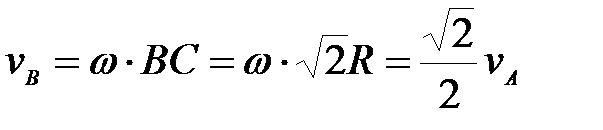 .
Б.
.
Б. 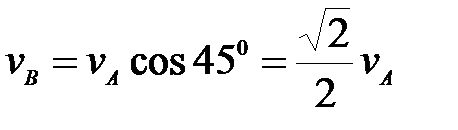 .
В.
.
В. 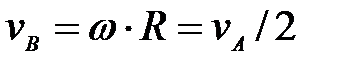 .
Г.
.
Г. 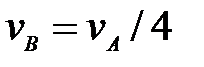 .
.
 -скорость груза 1 (рис.23).
-скорость груза 1 (рис.23).

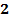
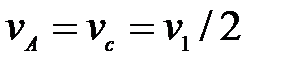 .
Б.
.
Б. 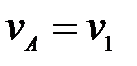 ,
, 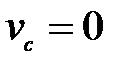 ;
В.
;
В. 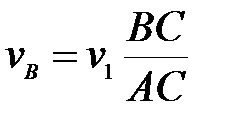 ;
; 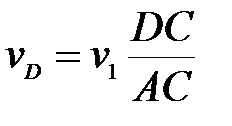 ;
Г.
;
Г. 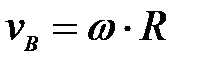 ;
; 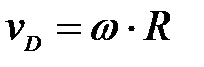 ;
;
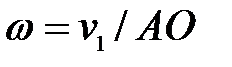 .
.
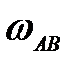 шатуна АВ, если в
данное мгновение известна скорость точки
шатуна АВ, если в
данное мгновение известна скорость точки 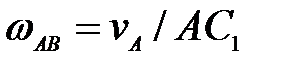 ; Б.
; Б. 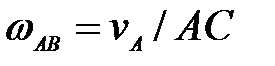 ;
;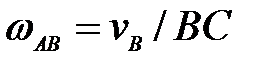 ,
, 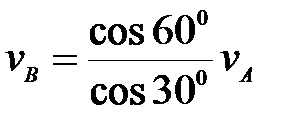 ; Г.
; Г. 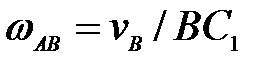 ,
, 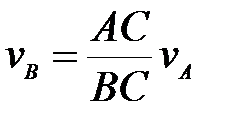 .
.
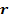
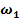
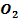
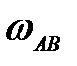 звена АВ, если известны угловая скорость
звена АВ, если известны угловая скорость 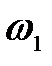 шкива 1, его радиус
шкива 1, его радиус 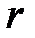 и
и 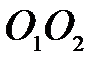 .
.
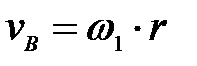 ;
; 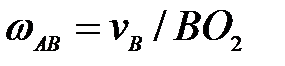 ;
;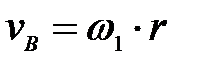 ;
; 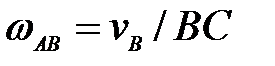 ;
;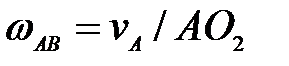 ;
; 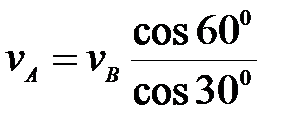 ;
;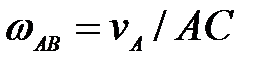 .
.
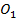
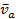
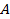
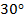
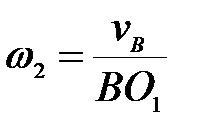 ;
; 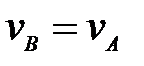 ;
; 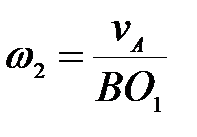 ;
;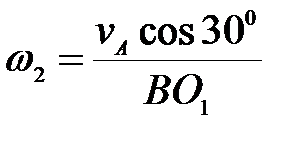 ;
;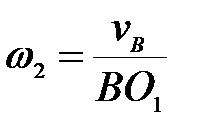 ;
; 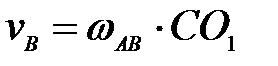 ;
; 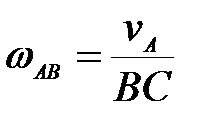 ;
; 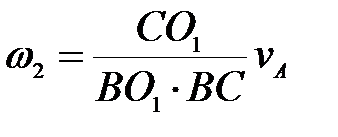 .
.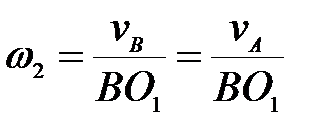 , т.к.
, т.к. 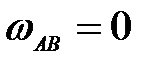 .
.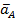
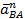
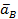
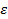
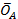
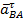
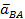
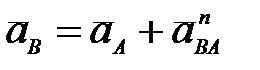 ;
;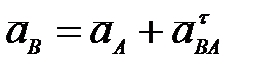 ;
;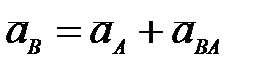 ;
;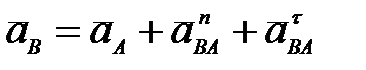 ;
;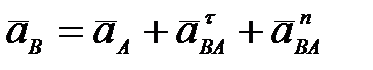 (рис. 28а));
(рис. 28а));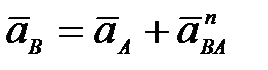 (рис. 28б));
(рис. 28б));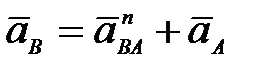 (рис. 28в));
(рис. 28в));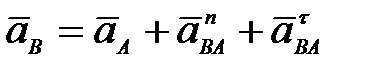 (рис. 28г)).
(рис. 28г)).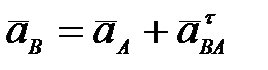 (рис. 29а)).
(рис. 29а)).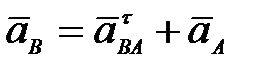 (рис. 29б)).
(рис. 29б)). (рис. 29в)).
(рис. 29в)).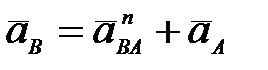 (рис. 29г)).
(рис. 29г)).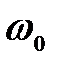 (рис.30). В каких случаях ускорение ползуна В определено верно?
(рис.30). В каких случаях ускорение ползуна В определено верно?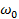
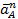
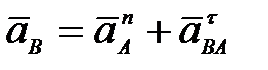 (рис. 30а). Б.
(рис. 30а). Б. 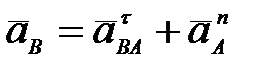 (рис. 30б).
(рис. 30б).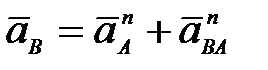 (рис. 30в). Г.
(рис. 30в). Г. 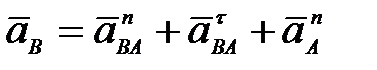 (рис. 30г).
(рис. 30г).
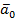
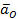
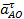
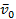
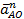
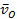
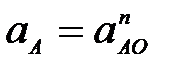 ;
; 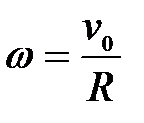 ;
; 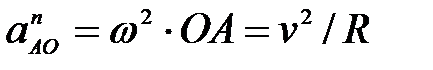 (рис. 31а).
(рис. 31а).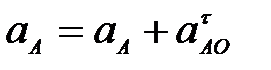 ;
; 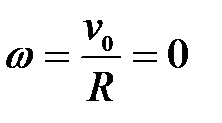 ;
; 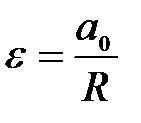 ;
; 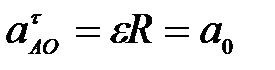 ;
; 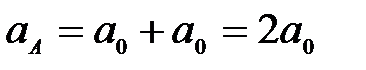 (рис. 31б);
(рис. 31б);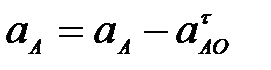 ;
; 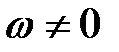 ;
; 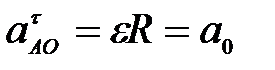 ;
; 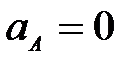 (рис. 31в));
(рис. 31в));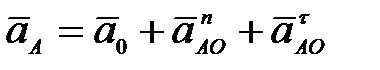 ;
; 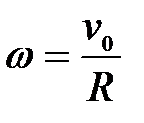 ;
; 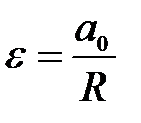 ;
; 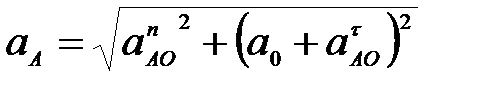 ;
; 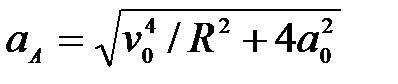 ; (рис. 31г));
; (рис. 31г));


