
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства главного вектора и главного момента
1 Модуль и направление Fгл не зависят от выбора центра приведения. 2 Величина и знак Мгл зависят от выбора центра приведения. 3 Главный вектор Fгл и равнодействующая F∑ системы сил векторно равны, но не эквивалентны. Частные случаи 1) Fгл = 0, Мгл Если главный вектор данной плоской системы сил равен нулю, а ее главный момент не равен нулю, то эта система эквивалентна паре, момент которой равен алгебраической сумме моментов всех данных сил относительно любой точки плоскости. 2) Fгл Если главный вектор данной плоской системы сил не равен нулю, а главный момент равен нулю, то эта система приводится к равнодействующей, равной по модулю и направлению главному вектору Fгл. 20 Различные случаи приведения ПСПРС 1. Fгл ≠ 0, Мгл ≠ 0. В этом случае система сил эквивалентна равнодействующей, которая равна по модулю главному вектору, параллельна ему и направлена в ту же сторону, но по другой линии действия. 2. Fгл ≠ 0, Мгл = 0. В этом случае система сил эквивалентна равнодействующей, линия действия которой проходит через центр приведения и совпадает с главным вектором. 3. Fгл = 0, Мгл ≠ 0. В этом случае система эквивалентна паре сил, т. е. она обладает лишь вращающим действием. 4. Fгл = 0, Мгл = 0. В этом случае система сил эквивалентна нулю, т. е. находится в равновесии. 31 Моменты инерции сечения (lx ly lp) Зависимость между ними Момент инерции – распространенная на всю площадь сумма произведений элементарных площадок dA на квадраты расстояний от них до этой оси. Осевые моменты инерции где ρ – расстояние от площадки dA до точки (полюса), относительно которого вычисляется полярный момент инерции. Полярный момент инерции связан с осевыми моментами инерции то есть для любой пары взаимно перпендикулярных осей, проходящих через полюс Центробежный момент инерции определяется интегралом произведений элементарных площадей на их расстояния до двух взаимно перпендикулярных осей Размерность моментов инерции – единицы длины в четвертой степени. Осевые и полярный момент инерции всегда положительны, центробежный момент инерции может принимать значения «+», «–» и ноль. Если фигура имеет ось симметрии, то относительно этой оси центробежный момент инерции равен нулю
Осевым моментом инерции сечения относительно оси x называется сумма произведений элементарных площадок Аналогично относительно оси у где
Полярным моментом инерции сечения относительно данной точки (полюса) называется сумма произведений элементарных площадок
где ρ – расстояние от площадки Осевой и полярный моменты инерции – величины всегда положительные, так как в формулы (6) и (7) координаты произвольной площадки входят в квадрате. Центробежным моментом инерции сечения относительно осей где Размерность всех моментов инерции – единица длины в четвертой степени (обычно Центробежный момент инерции может быть положительным, отрицательным и, в частном случае, равным нулю. Если взаимно перпендикулярные оси
Легко доказать, что полярный момент инерции относительно какой–либо точки равен сумме осевых моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту точку.
Следовательно,
|
||||||
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 600; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.186.164 (0.006 с.) |
 0
0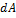 на квадрат их расстояний до данной оси, численно равная интегралу
на квадрат их расстояний до данной оси, численно равная интегралу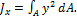 (6)
(6)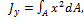
 — расстояние от элементарной площадки
— расстояние от элементарной площадки 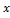 ,
,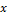 — расстояние от элементарной площадки
— расстояние от элементарной площадки  , (7)
, (7)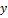 называется сумма произведений элементарных площадок
называется сумма произведений элементарных площадок  , (8)
, (8)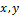 – расстояния от площадки
– расстояния от площадки  ).
).
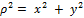 . Подставив это значение в выражение (7), получим
. Подставив это значение в выражение (7), получим
 .
.


