
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Part 3.Determination of the Acceleration of a Particle when its Motion is described by the Natural MethodСодержание книги
Поиск на нашем сайте In the natural method of describing motion vector The acceleration of a particle lies in the osculating plane Mrn, hence its projection on the binormal is zero (ab=0). Let the particle occupy a position M and have a velocity From the theorem of the projection of a vector sum (or difference) on an axis we obtain: Noting that projections of vector on parallel axes are equal, draw through point M 1 axes Mr’ and Mn’ parallel to Mr and Mn, respectively, and denote the angle between the direction of vector and the tangent Mr (this angle is called the angle of contiguity).
where k – the curvature of the curve at point M; R – the radius of curvature at point M. We see that Vr = V; Vn = 0; V1 r = V1 cos D f; V1 n =V1 sin D f. Hence
When D t tends to zero, D f and D S tends to zero too and V 1 tends to V. Then
Multiplying the numerator and denominator of the fraction under the limit sign an by D f D S, we find since Finally we obtain
We have thus proved that the projection of the acceleration of a particle on the tangent to the path is equal to the first derivative of the numerical value of the velocity, or the second derivative of the displacement S, with respect to time; the projection of the acceleration on the principal normal is equal to the second power of the velocity divided by the radius of curvature of the path at the given point of the curve, the projection of the acceleration on the binormal is zero (ab=0). The acceleration vector The relations obtained express that the tangential component of the acceleration is equal to the rate of change of the speed of the particle, while the normal component is equal to the square of the speed divided by the radius of curvature of the path at point P. Normal acceleration characterizes the change in direction of the velocity depending upon whether the speed of the particle increases or decreases, ar positive or negative, and the vector component The absolute or numerical value of the velocity is called the speed: speed is thus essentially a positive quantity.
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 107; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.39.85 (0.007 с.) |

 is determined from its projections on a set of coordinate axes Mrnb whose origin is at M and who move together with the body. These axes, called the axes of the natural trihedron (or velocity axes), are directed as follows: axis Mr along the tangent to the path in the direction of the positive displacement S, axis Mn along the normal in the osculating plane towards the inside of the path, and axis Mb perpendicular to the former two to form a right-hand set. The normal Mn, which lies in the osculating plane (or in plane of the curve itself if the curve is two-dimensional), is called the principal normal, and the normal Mb perpendicular to it is called the binormal.
is determined from its projections on a set of coordinate axes Mrnb whose origin is at M and who move together with the body. These axes, called the axes of the natural trihedron (or velocity axes), are directed as follows: axis Mr along the tangent to the path in the direction of the positive displacement S, axis Mn along the normal in the osculating plane towards the inside of the path, and axis Mb perpendicular to the former two to form a right-hand set. The normal Mn, which lies in the osculating plane (or in plane of the curve itself if the curve is two-dimensional), is called the principal normal, and the normal Mb perpendicular to it is called the binormal.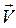 at time t, and at time t1=t+ D t let it occupy a position M 1 and have a velocity
at time t, and at time t1=t+ D t let it occupy a position M 1 and have a velocity 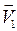 .
.
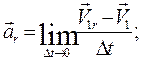
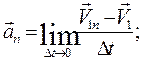

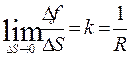

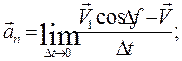
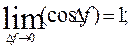
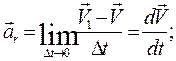
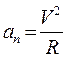 ,
,
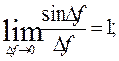
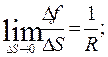
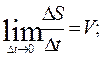
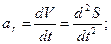

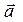 is the diagonal of a parallelogram constructed with the components
is the diagonal of a parallelogram constructed with the components 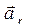 and
and 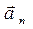 as its sides. As the components are mutually perpendicular, the magnitude of vector
as its sides. As the components are mutually perpendicular, the magnitude of vector 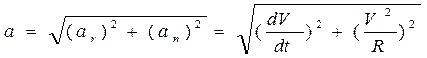 .
.


