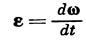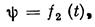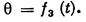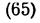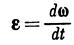Ex.1. Look at Appendices  1 and 2 and  read the following mathematical symbols and Greek letters.

     j = < KOx, y= < x1OK, q = < z1Oz,           

Let us investigate the motion of a body having a fixed point 0 with respect to a reference system o x1y1. Any body with a ball-and-socket joint is the illustration of such motion. Let us find the parameters that determine the position of a body having one fixed point. For this, assume the body is  rigidly attached to the trihedron Oxyz whose position defines the position of the body (Fig. 25).

Fig. 25

Line OK, along which planes Oxy and Ox1y1 intersect, is called the line of nodes. The position of the trihedron Oxyz, and hence of the body, with respect to the axes Ox1y1 is given by the angles: j = < KOx, y= < x1OK, q = < z1Oz.

These angles, called the Euler angles, are known by the following names, taken from celestial mechanics: j—the angle of proper rotation, y—angle of precession, q— angle of nutation. The positive directions are shown in Fig. 25 by arrows. A change in angle j indicates a rotation of the body around axis Oz (proper rotation), a change in angle y indicates a rotation around axis 0z1  (precession), and a change in angle q indicates a rotation around the line of nodes OK  (nutation).

To describe the body's motion, its position with respect to axes Ox1y1z1 must be known for any instant, i.e.,

Equations (65) define the law of motion and are called the equa­tions of motion of a rigid body about a fixed point.

To get a full picture of this type of motion, let us demonstrate the following theorem of Euler-d’Alembert: Any elementary displacement of a body having a fixed point represents an elementary rotation about an instantaneous axis of rotation through that point.

Let the body’s position be given by the angles j,y,q. Then its displacement in an elementary time interval dt can be represented as the resultant of a series of rotations through angles dj,dy  and dq   about axes Oz, Oz₁,and OK, respectively. Combined, the three rotations yield the true elementary displacement of the body.

Consider first the resultant displacement of the rotations about axes Oz and Oz₁ (Fig. 26). A rotation through angle dj, about axis Oz imparts to any point of the body in the plane zOz ₁ (inside angle z0z ₁ ) an elemen­tary displacement perpendicular to the plane and equal in magnitude to h1dj, where h1 is the distance of the point from axis Oz. Simultaneously, in the ro­tation about axis Oz1, the point will receive an oppositely directed displace­ment of magnitude h2dj. Accordingly, within angle zOz₁, there will always be a point B for which

h1dj = h2dy   and whose displacement is zero (if the direc­tion of rotation is opposite to that shown in Fig. 26, the point lies outside angle zOz₁). Hence we conclude that the body's elementary displacement resulting from the rotations about axes Oz and Oz1 is the same as the displacement of a body with two stationary points 0 and B, i.e., it is an elementary rotation about axis OB through point 0.

 

 

Fig. 26

By the same reasoning, the elementary rotations about axes OB and OK are equivalent to an elementary rotation about an axis OP through point 0 (Fig. 26), and the theorem is proved.

Axis OP is called the instantaneous axis of rotation; an elementary rotation of the body about it brings the body into a neighbouring position infinitesimally close to the given position; the velocities of all points of the body lying on the instantaneous axis of rotation are zero. Unlike a fixed axis, the instantaneous axis of rotation con­tinuously changes its direction in space and in the body. The rota­tion about axis OP, which brought the body into the neighbouring position, is followed by a rotation about the new instantaneous axis of rotation OP1, etc. Thus, the motion of a rigid body about a fixed point is compounded of a series of consecutive elementary rotations about instantaneous axes of rotation through that fixed point (Fig. 26).

Let us examine the kinematics characteristics of this motion.

(1) The angular velocity w with which a body makes an elementa­ry rotation about the instantaneous axis of rotation is called the instantaneous angularvelocity of the body. It can be denoted bya vector w directed along axis OP. As the direction of axis OP changes continuously, vector w changes with time both in magnitude and direction, and its tip A describes a curve AD in space, which is the hodograph of vector w (Fig. 27).

Fig. 27

 

(2) The instantaneous angular acceleration of a body, which characterizes the time ra­te of change of the angular velocity w both in magnitude and direction, is a vector qu­antity

Comparing this expression with the equa­tion v == dr/dt, we conclude that the angular acceleration e can be computed as the velocity with which the tip of vector w moves along curve AD (see Fig. 27). Specifi­cally, the direction of e coincides with the direction of the tangent to curve AD at the respective point. Consequently, unlike the case of rotation about a fixed axis, the direction of vector e does not coincide with that of vector w.

Vectors w and e are the basic kinematic characteristics of the motion of a body having a fixed point. They can be computed when the equations of motion (65) are known.

Comprehension  check.