
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ex. 9 . Translate the following phrases into English.
Пусть точка занимает положение; в данный момент времени; по отношению ко времени; соответствующие координаты точки; положительное перемещение; провести ось через точку; обозначить угол между; радиус кривой; время стремится к нулю; полученное отношение; абсолютное и числовое значение скорости.
Ex. 10. Translate into English. 1. Эти составляющие взаимно перпендикулярны. 2. Скорость точки может увеличиваться или уменьшаться с течением времени. 3. Этот угол называется смежным. 4. Эта ось перпендикулярна к двум другим осям. 5. Вектор ускорения - это диагональ параллелограмма, сторонами которого являются составляющие 6. Вектор
Unit 5. Tangential and Normal Accelerations of a Particle.
Learn the following words and word combinations by heart:
Ex.1. Look at Appendix 1 and read the following mathematical symbols and Greek letters. τ, w, Δφ,
We can already compute the acceleration vector The acceleration
Fig. 6
Let us calculate the projection of
Let us now express this equation in terms of the projections of the vectors on the axes M τand Mn through point M (see Fig. 6). From the theorem of the projection of a vector sum (or difference) on an axis we obtain:
Noting that projections of a vector on parallel axes are equal, draw through point M1 axes Mτ' and Mn' parallelto Mτ and Mn respectively, and denote the angle between the direction of vector
It will be recalled that the limit of the ratio of the angle of contiguity Δφ to the arc
From the diagram in Fig. 6, we see that the projections of vectors v t = v, vn = 0, v1 t = v1 cos D j, v1n = sin D j, where v and v1 are the numerical values of the velocity of the particle at instants t and t1. Hence,
It will be noted that when Hence, taking into account that We shall transform the right-hand side of the equation for wn in such a way so that it includes ratios with known limits. For this purpose, multiplying the numerator and denominator of fraction under the limit sign by D j D s, we find:
since, when
Finally we obtain We have thus proved that the projection of acceleration of a particle on tangent to the path is equal to the first derivative of numerical value of the velocity, or the second derivative of the displacement (the arc coordinate) s, with respect to time; the projection of the acceleration on the principal normal is equal to the second power of the velocity divided by the radius of curvature of the path at the given point of curve, the projection of acceleration on the binormal is zero (wb = 0). This is an important theorem of particle kinematics. When particle M is moving in one plane, the tangent M t sweepsaround the binormal Mb with an angular velocity Wn = v w (24.1) i.e. normal acceleration equals the product of a particle’s velocity by angular velocity of the sweep of tangent to the path. Fig. 7
Lay off vectors The acceleration vector
Thus, if the motion of a particle is described by the natural method and the path (and, consequently, the radius of curvature at any point) and the equations of motion (20) are known, from Eqs. (22), (24), and (25) we can determine the magnitude and direction of the velocity and acceleration vectors of the particle for any instant.
Comprehension check.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.96.102 (0.014 с.) |
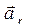 и
и 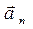 .
. ., sin Dj, wn>0,
., sin Dj, wn>0,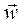 according to its projections on stationary coordinate axes Oxyz. In the natural method of describing motion, vector
according to its projections on stationary coordinate axes Oxyz. In the natural method of describing motion, vector 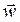 is determined from its projections on a set of coordinate axes M τ nb whose origin is at M and who move together with the body (Fig. 6).
is determined from its projections on a set of coordinate axes M τ nb whose origin is at M and who move together with the body (Fig. 6). of a particle lies in the osculating plane, i.e., plane M τ n, hence the projection of vector
of a particle lies in the osculating plane, i.e., plane M τ n, hence the projection of vector 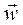 on the binormal is zero (wb = 0).
on the binormal is zero (wb = 0).
 at any time t, and at time t1=t+Δt let it occupy a position M1 and have a velocity
at any time t, and at time t1=t+Δt let it occupy a position M1 and have a velocity 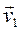 . Then, by virtue of the definition,
. Then, by virtue of the definition,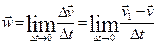
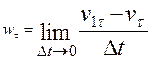 ,
,  .
. = D s defines the curvature k of the curve at the point M. As the curvature is the inverse of the radius of curvature r at M, we have:
= D s defines the curvature k of the curve at the point M. As the curvature is the inverse of the radius of curvature r at M, we have: .
.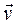 and
and  on the axes M t and Mn are
on the axes M t and Mn are ,
,  .
.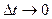 , point M1 approaches M indefinitely, simultaneously
, point M1 approaches M indefinitely, simultaneously  ,
, 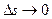 and
and 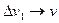 .
.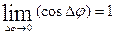 , we obtain for w t the expression
, we obtain for w t the expression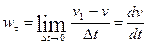 .
.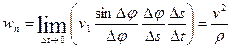 , (23)
, (23)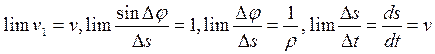 .
.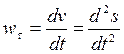 ,
, 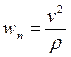 . (24)
. (24)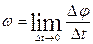 . By introducing this quantity into Eq. (23) we can obtain one more equation for calculating wn that is frequently used in practice:
. By introducing this quantity into Eq. (23) we can obtain one more equation for calculating wn that is frequently used in practice:
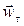 and
and 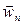 , i.e. the normal and tangential components of the acceleration, along the tangent M t and the principal normal Mn, respectively (Fig. 7). The component
, i.e. the normal and tangential components of the acceleration, along the tangent M t and the principal normal Mn, respectively (Fig. 7). The component 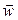 and its angle m to the normal Mn are given by the equations:
and its angle m to the normal Mn are given by the equations: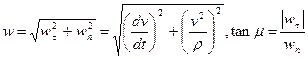 (25)
(25)


