
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ex.1. Look at Appendix 1 and read the following mathematical symbols.
In kinematics, as in statics, we shall regard all solids as rigid bodies, i.e., we shall assume that the distance between any two points of a body remains the same during the whole period of motion.
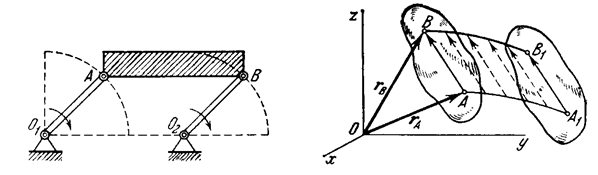
Fig. 8 Fig. 9
Problems of kinematics of rigid bodies are basically of two types: (1) definition of the motion and analysis of the kinematics characteristics of the motion of a body as a whole; (2) analysis of the motion of every point of the body in particular. We shall begin with the consideration of the motion of translation of a rigid body. Translation of a rigid body is such a motion in which any straight line through the body remains continually parallel to itself. Translation should not be confused with rectilinear motion. In translation the particles of a body may move on any curved paths. The properties of translational motion are defined by the following theorem: In translational motion, all the particles of a body move along similar paths (which will coincide if superimposed) and have at any instant the same velocity and acceleration. To prove the theorem, consider a rigid body translated with reference to a system of axes Oxyz. Take two arbitrary points A and B on the body whose positions at time t are specified by radius vectors The length of To determine the velocities of points A and B, we differentiate both parts of Eq. (35) with respect to time. We have
But the derivative of the constant vector
i.e., at any instant the velocities of points A and B are equal in magnitude and direction. Again, differentiating both sides of the equation with respect to time, we obtain
Hence, at any instant the accelerations of A and B are equal in magnitude and direction. As points A and B are arbitrary, it follows that the paths and the velocities and accelerations of all the points of a body at any instant are the same, which proves the theorem. It follows from the theorem that the translational motion of a rigid body is fully described by the motion of any point belonging to it. Thus, the analysis of translational motion of a rigid body is reduced to the methods of particle kinematics examined before. The common velocity
Comprehension check.
|
||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 75; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.34.87 (0.004 с.) |
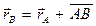 ,
,  ,
, 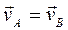
 and
and  (Fig. 9). Draw a vector
(Fig. 9). Draw a vector 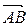 joining the two points. It is evident that
joining the two points. It is evident that (35)
(35)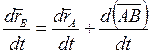 .
.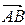 is zero while the derivatives of vectors
is zero while the derivatives of vectors  with respect to time give the velocities of points A and B. Thus we find that
with respect to time give the velocities of points A and B. Thus we find that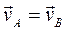 ,
, or
or 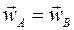 .
.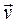 of all the points of a body in translational motion is called the velocity of translation, and the common acceleration w is called the acceleration of translation. Vectors
of all the points of a body in translational motion is called the velocity of translation, and the common acceleration w is called the acceleration of translation. Vectors 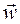 can, obviously, be shown as applied at any point of the body.
can, obviously, be shown as applied at any point of the body.


