
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ministry of education and science of ukraineСтр 1 из 24Следующая ⇒
MINISTRY OF EDUCATION AND SCIENCE OF UKRAINE DONETSK NATIONAL TECHNICAL UNIVERSITY METHODIC INSTRUCTION FOR THE COURSE ON THEORETICAL MECHANICS IN ENGLISH
Considered on the meeting of the English language chair Record No 6, 08. 02. 06
Considered on the meeting of the chair of Theoretical Mechanics Record No 10, 25.04.06
Approved by the Educational and Methodical Council of DonNTU Record No 2, 24.05.2006
Donetsk - 2006 Methodic instruction for the course on Theoretical Mechanics in English. Methodic instruction for the students of all specialities// Authors: Kuksina O.I., Ignatov A.V. // - Donetsk: Donetsk National Technical University, 2006 – 117 p.
Methodic instruction for the course on Theoretical Mechanics in English. Methodic instruction on theoretical mechanics are intended for reading by the students of all specialities.
Authors: Senior Lecturer Kuksina O.I., Candidate of Sciences, ass. Professor Ignatov A.V.
The reviewers: Doctor of Sciences (technology), Professor Bulgakov Y.F., ass. Professor Poverennij A.I.
МIНIСТЕРСТВО ОСВIТИ I НАУКИ УКРАЇНИ ДОНЕЦЬКИЙ НАЦIОНАЛЬНИЙ ТЕХНIЧНИЙ УНIВЕРСИТЕТ МЕТОДИЧНІ ВКАЗІВКИ З ВИВЧЕННЯ КУРСУ ТЕОРЕТИЧНОЇ МЕХАНІКИ НА АНГЛІЙСЬКІЙ МОВІ Розглянуто на засіданні кафедри англійської мови Протокол № 6 від 08.02. 06. Розглянуто на засіданні кафери «Теоретична механіка» Протокол № 10 від 25.04.2006. Затверджено учбово-методичною радою ДонНТУ Протокол № 2 від 24.05. 2006.
Донецьк - 2006
Методичні вказівки з вивчення курсу теоретичної механіки на англійській мові. Методичні вказівки для студентів усіх спеціальностей. // Укладачі: Куксіна О.І., Ігнатов О.В. // -Донецьк: ДонНТУ, 2006 – 117 с.
Методичні вказівки з вивчення курсу теоретичної механіки на англійській мові. Методичні вказівки по теоретичній механіці призначені для читання студентами усіх спеціальностей.
Укладачі: старший викладач Куксіна О.І., кандидат технічних наук, доцент Ігнатов О.В.
Рецензенти: доктор технічних наук, професор Булгаков Ю.Ф., доцент Поверенний А. І. Contents Page
English-Russian Vocabulary | 100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Literature | 118 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Introduction. The texts for reading in the methodic instruction are compounded by the authors on a foundation of the known references on theoretical mechanics / 1- 9 / and are intended for the students learning course of theoretical mechanics in English.
Unit 1.
Ex.3. Complete the following sentences with the information from the text.
1. Theoretical or general mechanics treats of…
2. The design and calculation of specific structures are based on…
3. Mechanical motion is…
4. The physical measure of mechanical interaction is…
5. The general course of theoretical mechanics treats of …
Kinematics. Kinematics of a Particle.
Text 1. Kinematics
Learn the following words and word combinations by heart:
| аcceleration | ускорение |
| be at rest change with time consequently consider define | находиться в состоянии покоя изменяться с течением времени следовательно считать, рассматривать определять, давать точное определение, характеризовать |
| determine | определять, устанавливать, измерять, вычислять |
| frame of reference locate | система отчета располагать, размещать, определять местоположения |
| path | путь, траектория |
| remain constant specify a position | оставаться постоянным, неизменным определить положение |
| take into account | принимать во внимание |
| velocity | скорость |
| algebraic ~ angular ~ | алгебраическая скорость угловая скорость |
| average ~ | средняя скорость |
| instantaneous ~ linear ~ zero ~ | мгновенная скорость линейная скорость нулевая скорость |
| with respect to = w r t | по отношению к… |
Kinematics is the section of mechanics, which treats of the geometry of the motion of bodies without taking into account their inertia (mass) or the forces acting on them.
By motion in mechanics is meant the relative displacement with time of a body in space with respect to other bodies.
|
|
In order to locate a moving body (or particle) we assume a coordinate system, which we call the frame of reference or reference system, to be fixed relative to the body with respect to which the motion is being considered. If the coordinates of all the points of a body remain constant within a given frame of reference, the body is said to be at rest relative to that reference system. If, on the other hand, the coordinates of any points of the body change with time, the body is said to be in motion relative to the given frame of reference (and consequently, relative to a body which is fixed with respect to the frame of reference).
To describe the motion, or the law of motion, of a given body (particle) kinematically means to specify the position of that body (particle) relative to a given frame of reference for any moment of time. The principal problem of kinematics is that of determining all the kinematics characteristics of the motion of a body as whole or of any of its particles (path, velocity, acceleration etc.) when the law of motion for the given body is known.
Comprehension check.
Ex.1. Answer the following questions:
1. What does motion mean in mechanics?
2. When is the body said to be at rest?
3. What happens when the coordinates of any points of a body change with time?
4. What is the principal problem of kinematics?
Fig. 2
Velocity of a Particle.
Learn the following words and word combinations by heart:
| appreciate | оценивать |
| arc of a path as | дуга пути, дуга траектории так как.. |
| be called be equal to = equal | называться равняться …., быть равным |
| be tangent to a path | быть касательной к траектории пути |
| characterize speed | характеризовать скорость |
| chord | хорда |
| determination | определение |
| derivative of finally | производная в конце концов, в конечном счете |
| numerical value of obviously | цифровое значение … явно, очевидно |
| precisely rapidity ratio | точно, определенно, именно скорость соотношение, коэффициент |
| readily | легко, просто, без труда |
| scalar function secant | скалярная функция секущая, секанс |
| sign of … is the same as that of take into account | знак …такой же самый, как знак принимать во внимание |
| tangent | касательная; тангенс, касательная линия |
| tend to | стремиться к … |
| towards | по направлению к…, к |
Comprehension check.
Unit 4.
Comprehension check.
Unit 5.
Fig. 6
Let us calculate the projection of 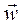 on the other two axes. Let the particle occupy a position M and have a velocity
on the other two axes. Let the particle occupy a position M and have a velocity  at any time t, and at time t1=t+Δt let it occupy a position M1 and have a velocity
at any time t, and at time t1=t+Δt let it occupy a position M1 and have a velocity 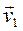 . Then, by virtue of the definition,
. Then, by virtue of the definition,
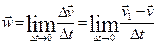
Let us now express this equation in terms of the projections of the vectors on the axes M τand Mn through point M (see Fig. 6). From the theorem of the projection of a vector sum (or difference) on an axis we obtain:
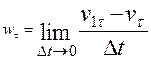 ,
,  .
.
Noting that projections of a vector on parallel axes are equal, draw through point M1 axes Mτ' and Mn' parallelto Mτ and Mn respectively, and denote the angle between the direction of vector 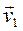 and the tangent Mτ by the symbol Δφ. This angle between the tangents to the curve at points M and M1 is called the angle of contiguity.
and the tangent Mτ by the symbol Δφ. This angle between the tangents to the curve at points M and M1 is called the angle of contiguity.
It will be recalled that the limit of the ratio of the angle of contiguity Δφ to the arc  = D s defines the curvature k of the curve at the point M. As the curvature is the inverse of the radius of curvature r at M, we have:
= D s defines the curvature k of the curve at the point M. As the curvature is the inverse of the radius of curvature r at M, we have:
 .
.
From the diagram in Fig. 6, we see that the projections of vectors 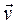 and
and  on the axes M t and Mn are
on the axes M t and Mn are
v t = v, vn = 0,
v1 t = v1 cos D j, v1n = sin D j,
where v and v1 are the numerical values of the velocity of the particle at instants t and t1. Hence,
 ,
,  .
.
It will be noted that when 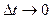 , point M1 approaches M indefinitely, simultaneously
, point M1 approaches M indefinitely, simultaneously  ,
, 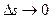 and
and 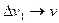 .
.
Hence, taking into account that 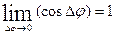 , we obtain for w t the expression
, we obtain for w t the expression
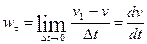 .
.
We shall transform the right-hand side of the equation for wn in such a way so that it includes ratios with known limits. For this purpose, multiplying the numerator and denominator of fraction under the limit sign by D j D s, we find:
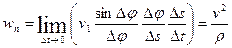 , (23)
, (23)
since, when 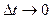 , the limits of each of the cofactors inside the brackets are as follows:
, the limits of each of the cofactors inside the brackets are as follows:
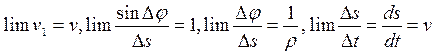 .
.
Finally we obtain
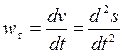 ,
, 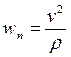 . (24)
. (24)
We have thus proved that the projection of acceleration of a particle on tangent to the path is equal to the first derivative of numerical value of the velocity, or the second derivative of the displacement (the arc coordinate) s, with respect to time; the projection of the acceleration on the principal normal is equal to the second power of the velocity divided by the radius of curvature of the path at the given point of curve, the projection of acceleration on the binormal is zero (wb = 0). This is an important theorem of particle kinematics.
|
|
When particle M is moving in one plane, the tangent M t sweepsaround the binormal Mb with an angular velocity 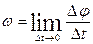 . By introducing this quantity into Eq. (23) we can obtain one more equation for calculating wn that is frequently used in practice:
. By introducing this quantity into Eq. (23) we can obtain one more equation for calculating wn that is frequently used in practice:
Wn = v w (24.1)
i.e. normal acceleration equals the product of a particle’s velocity by angular velocity of the sweep of tangent to the path.

Fig. 7
Lay off vectors 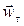 and
and 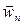 , i.e. the normal and tangential components of the acceleration, along the tangent M t and the principal normal Mn, respectively (Fig. 7). The component
, i.e. the normal and tangential components of the acceleration, along the tangent M t and the principal normal Mn, respectively (Fig. 7). The component 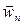 is always directed along the inward normal, as wn>0, while the component
is always directed along the inward normal, as wn>0, while the component 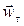 can be directed either in the positive or in the negative direction of axis M t, depending on the sign of the projection w t (see Figs. 7 a and b).
can be directed either in the positive or in the negative direction of axis M t, depending on the sign of the projection w t (see Figs. 7 a and b).
The acceleration vector 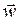 is the diagonal of a parallelogram constructed with the components
is the diagonal of a parallelogram constructed with the components 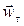 and
and 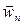 as its sides. As the components are mutually perpendicular, the magnitude of vector
as its sides. As the components are mutually perpendicular, the magnitude of vector 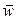 and its angle m to the normal Mn are given by the equations:
and its angle m to the normal Mn are given by the equations:
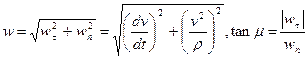 (25)
(25)
Thus, if the motion of a particle is described by the natural method and the path (and, consequently, the radius of curvature at any point) and the equations of motion (20) are known, from Eqs. (22), (24), and (25) we can determine the magnitude and direction of the velocity and acceleration vectors of the particle for any instant.
Comprehension check.
Unit 6.
Comprehension check.
Unit 7.
Fig. 10
Eq. (36) describes the rotational motion of a rigid body.
The principal kinematic characteristics of the rotation of a rigid body are its angular velocity 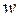 and angular acceleration
and angular acceleration 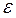 .
.
If in an interval of time ∆t = t1 – t a body turns through an angle ∆ φ = φ 1- φ, the average angular velocity of the body in the given time interval is
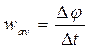 .
.
The angular velocity of a body at a given time t is the value towards which  tends when the time interval ∆t tends to zero:
tends when the time interval ∆t tends to zero:
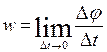 or
or 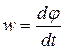 . (37)
. (37)
Thus, the angular velocity of a body at a given time is equal in magnitude to the first derivative of the angle of rotation with respect to time. Eq. (37) also shows that the value of 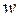 is equal to the ratio of the infinitesimal angle of rotation d φ to the corresponding time interval dt. The sign of
is equal to the ratio of the infinitesimal angle of rotation d φ to the corresponding time interval dt. The sign of 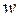 specifies the direction of the rotation. It will be noticed that
specifies the direction of the rotation. It will be noticed that 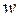 >0 when the rotation is counterclockwise, and
>0 when the rotation is counterclockwise, and 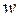 <0 when the rotation is clockwise. The dimension of angular velocity, if the time is measured in seconds, is
<0 when the rotation is clockwise. The dimension of angular velocity, if the time is measured in seconds, is
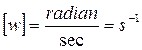 ,
,
as the radian is a dimensionless unit.
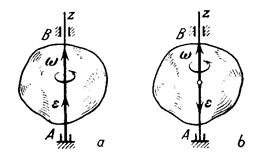
Fig. 11
The angular velocity of a body can be denoted by a vector 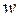 of magnitude
of magnitude 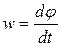 along the axis of rotation of the body in the direction from which the rotation is seen as counterclockwise (see Fig. 11). Such a vector simultaneously gives the magnitude of the angular velocity, the axis of rotation, and the sense of rotation about that axis.
along the axis of rotation of the body in the direction from which the rotation is seen as counterclockwise (see Fig. 11). Such a vector simultaneously gives the magnitude of the angular velocity, the axis of rotation, and the sense of rotation about that axis.
Angular acceleration characterizes the time rate of change of the angular velocity of a rotating body.
If in a time interval ∆t=t1–t the change of angular velocity of a body is 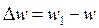 , the average angular acceleration of the body in that interval of time is
, the average angular acceleration of the body in that interval of time is 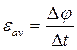 .
.
The angular acceleration at a given time t is the value towards which 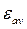 tends when the time interval ∆t tends to zero. Thus,
tends when the time interval ∆t tends to zero. Thus,
 ,
,
or, taking into account Eq. (37)
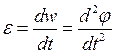 . (38)
. (38)
Thus, the angular acceleration of a body at a given time is equal in magnitude to the first derivative of the angular velocity, or the second derivative of the angular displacement, of the body with respect to time. The dimension of angular acceleration is 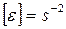 .
.
|
|
If the angular velocity increases in magnitude, the rotation is accelerated, if it decreases, the rotation is retarded. It will be readily noticed that the rotation is accelerated when 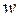 and
and 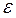 are of the same sign and retarded when they are of different sign.
are of the same sign and retarded when they are of different sign.
By analogy with angular velocity, the angular acceleration of a body can be denoted by a vector 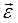 along the axis of rotation. The direction of
along the axis of rotation. The direction of 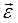 coincides with that of
coincides with that of 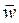 when the rotation is accelerated (Fig. 11a), and is of opposite sense when the rotation is retarded (Fig. 11b).
when the rotation is accelerated (Fig. 11a), and is of opposite sense when the rotation is retarded (Fig. 11b).
Comprehension check.
Unit 8.
Fig. 12
In order to determine the acceleration of point M, we apply equations

 .
.
Substituting the expression for v from Eq. (44), we obtain
 ,
, 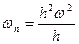 ,
,
and finally
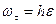 ,
, 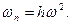 (45)
(45)
The tangential acceleration wt, is tangent to the path (in the direction of the rotation if it is accelerated and in the reverse direction if it is retarded); the normal acceleration wn is always directed along the radius h towards the axis of rotation (Fig. 13a).
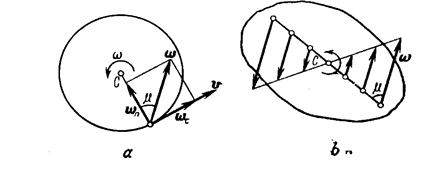
Fig. 13
The total acceleration of point M is

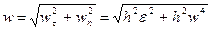 ,
,
or
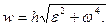 (46)
(46)
The inclination of the vector of total acceleration to the radius of the circle described by the point is specified by the angle μ, given by the equation
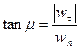 .
.
Substituting the expressions of wτ, and wn from Eqs. (45), we obtain
 . (47)
. (47)
Since at any given instant s and m are each the same for all the points of the body, it follows from Eqs. (46) and (47) that the accelerations of all the points of a rotating rigid body are proportional to their distance from the axis of rotation and make the same angle μ, with the radii of the circles described by them (Fig. 13b).
Eqs. (44)-(47) make it possible to determine the velocity and acceleration of any point of a body if the equation of rotation of the body and the distance of the given point from the axis of rotation is known. With these formulas, knowing the motion of any single point of a body, it is possible to determine the motion of any other point and the characteristics of the motion of the body as a whole.
Comprehension check.
Unit 9.
Plane Motion of a Rigid Body.
Fig. 16
Let us first translate the body so that pole A occupies position  (line A1B1, occupies position A2B1') and than turn the section about pole A2, through angle ∆φ1. In the same way we can move the body from position II to some new position III, etc. We conclude that the plane motion of a rigid body is a combination of a translation, in which all the points move in the same way as the pole A, and of a rotation about that pole.
(line A1B1, occupies position A2B1') and than turn the section about pole A2, through angle ∆φ1. In the same way we can move the body from position II to some new position III, etc. We conclude that the plane motion of a rigid body is a combination of a translation, in which all the points move in the same way as the pole A, and of a rotation about that pole.
The translational component of plane motion can, evidently, be described by the first two of Eqs. (48), and the rotational component by the third.
The principal kinematics characteristics of this type of motion are the velocity and acceleration of translation, each equal to the velocity and acceleration of the pole (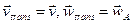 ) and the angular velocity and angular acceleration of the rotation about the pole. The values of these characteristics can be found for any time t from Eqs. (48).
) and the angular velocity and angular acceleration of the rotation about the pole. The values of these characteristics can be found for any time t from Eqs. (48).
In analyzing plane motion, we are free to choose any point of the body as the pole. Let us consider a point C as a pole instead of A and determine the position of the line CD making an angle φ1 with axis x (Fig. 17). The characteristics of the translatory component of the motion would have been different, for in the general case 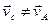 and
and  (otherwise the motion would be that of pure translation). The characteristics of the rotational component of the motion remain, however, the same. For, drawing CB, parallel to AB, we find that at any instant of time angle φ1 = φ –a, where a = const. Hence,
(otherwise the motion would be that of pure translation). The characteristics of the rotational component of the motion remain, however, the same. For, drawing CB, parallel to AB, we find that at any instant of time angle φ1 = φ –a, where a = const. Hence,
 ,
,  ,
,
This result can also be obtained from an examination of Fig. 16: whatever point is taken as the pole, to carry section S from position I to position II line A1B1 must be made parallel to A2B2, i.e., the section must be rotated around any pole through the same angle ∆φ1, equal to the angle between the two lines. Hence, the rotational component of motion does not depend on the position of the pole.
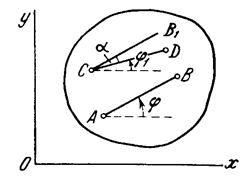
Fig. 17
Comprehension check.
Unit 10.
Fig. 18
Eqs. (49) describes the motion of point M in plane Oxy and at the same time gives the equation of the point’s path in parametric form. The usual equation of the path can be obtained by eliminating time t from Eqs. (49).
|
|
If the body under consideration is part of a mechanism, the path of any point M of the body can be determined by expressing the coordinates of the point in terms of a parameter specifying the position of the mechanism and then eliminating that parameter. In this case the equations of motion (48) are not necessary.
Comprehension check.
Fig. 19 Fig. 20
In this equation 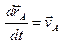 is equal to the velocity of pole A; the quantity
is equal to the velocity of pole A; the quantity  is equal to the velocity
is equal to the velocity 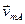 of point M at
of point M at 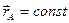 ., i.e., when A is fixed or, in other words, when the body (or, strictly speaking, its section S) rotates about pole A. It thus follows from the preceding equation that
., i.e., when A is fixed or, in other words, when the body (or, strictly speaking, its section S) rotates about pole A. It thus follows from the preceding equation that
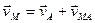 . (50)
. (50)
The velocity of rotation 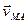 of point M about pole A is
of point M about pole A is
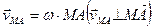 , (51)
, (51)
where ω is the angular velocity of the rotation of the body. Thus, the velocity of any point M of a body is the geometrical sum of the velocity of any other point A taken as the pole and the velocity of rotation of point M about the pole.
The magnitude and direction of the velocity  are found by constructing a parallelogram (Fig. 20).
are found by constructing a parallelogram (Fig. 20).
Fig. 21
One of these methods is given by the theorem: The projections of the velocities of two points of a rigid body on the straight line joining those points are equal.
Consider any two points A and B of a body. Taking point A as the pole (Fig. 21) we have from Eq. (50) 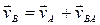 . Projecting both members of the equation on AB and taking into account that vector
. Projecting both members of the equation on AB and taking into account that vector  is perpendicular to AB, we obtain:
is perpendicular to AB, we obtain:
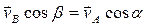 , (52)
, (52)
and the theorem is proved. This result offers a simple method of determining the velocity of any point of a body if the direction of motion of that point and the velocity of any other point of the same body are known.
Comprehension check.
Verbs
Nouns
Ex. 7. Complete the following table:
| Noun | Verb | Adjective |
| descriptive | ||
| investigate | ||
| quantitative | ||
| acceleration | ||
| equation | ||
| construct | ||
| computation | ||
| straight |
Unit 11.
Fig. 22
If, now, we take a point P as the pole at time t, the velocity of point A will, by Eq. (50), be
 ,
,
as  . The same result can be obtained for any other point of the body. Thus, the velocity of any point of a body lying in section S is equal to the velocity of its rotation about the instantaneous centre of zero velocity P. From Eqs. (51) we have
. The same result can be obtained for any other point of the body. Thus, the velocity of any point of a body lying in section S is equal to the velocity of its rotation about the instantaneous centre of zero velocity P. From Eqs. (51) we have
 , etc. (53)
, etc. (53)
It also follows from Eqs. (53) that
 , (54)
, (54)
i.e., that the velocity of any point of a body is proportional to its distance from the instantaneous centre of zero velocity.
These results lead to the following conclusions:
(1) To determine the instantaneous centre of zero velocity, it is sufficient to know the directions of the velocities  and
and 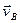 of any two points A and B of a section of a body (or their paths); the instantaneous centre of zero velocity lies at the intersection of the perpendiculars erected from points A and B to their respective velocities, or to the tangents to their paths.
of any two points A and B of a section of a body (or their paths); the instantaneous centre of zero velocity lies at the intersection of the perpendiculars erected from points A and B to their respective velocities, or to the tangents to their paths.
(2) To determine the velocity of any point of a body, it is necessary to know the magnitude and direction of the velocity of any point A of that body and the direction of the velocity of another point B of the same body. Then, by erecting from points A and B perpendiculars to  and
and 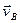 , we obtain the instantaneous centre of zero velocity P and, from the direction of
, we obtain the instantaneous centre of zero velocity P and, from the direction of  , the sense of rotation of the body. Next, knowing
, the sense of rotation of the body. Next, knowing  , we can find from Eq. (54) the velocity
, we can find from Eq. (54) the velocity  of any point M of the body. Vector
of any point M of the body. Vector  is perpendicular to
is perpendicular to 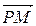 in the direction of the rotation.
in the direction of the rotation.
(3) The angular velocity of a body, as can be seen from Eqs. (53), is at any given instant equal to the ratio of the velocity of any point belonging to the section S’ to its distance from the instantaneous centre of zero velocity P:
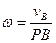 (55)
(55)
Let us evolve another expression for ω. It follows from Eqs. (50) and (51) that 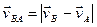 and
and 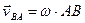 whence
whence
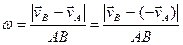 . (56)
. (56)
When  = 0 (point A is the instantaneous centre of zero velocity), Eq. (56) transforms into Eq. (55).
= 0 (point A is the instantaneous centre of zero velocity), Eq. (56) transforms into Eq. (55).
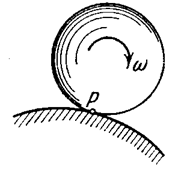
Fig. 23
Eqs. (55) and (56) give the same quantity, it follows that the rotation of the section S about either point A or point P takes place with the same angular velocity.
It is easy to verify that both equations give the same answer.
Let us consider some special cases of the instantaneous centre of zero velocity.
(a) If plane motion is performed by a cylinder rolling without slipping along a fixed cylindrical surface, the point of contact P (for the section shown in Fig. 23) is momentarily at rest and, consequently, is the instantaneous centre of zero velocity ( because if there is no slipping, the contacting points of both bodies must have the same velocity, and the second body is motionless). An example of such motion is that of a wheel running on a rail.
because if there is no slipping, the contacting points of both bodies must have the same velocity, and the second body is motionless). An example of such motion is that of a wheel running on a rail.
(b) If the velocities of points A and B of the body are parallel to each other, and AB is not perpendicular to  (Fig. 24 a) the instantaneous centre of zero velocity lies in infinity, and the velocities of all points are parallel to
(Fig. 24 a) the instantaneous centre of zero velocity lies in infinity, and the velocities of all points are parallel to  . From the theorem of the projections of velocities it follows that
. From the theorem of the projections of velocities it follows that  , i.e.,
, i.e., 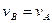 ; the result is the same for all other points of the body. Consequently, in this case the velocities of all points of the body are equal in magnitude and direction at every instant, i.e., the instantaneous distribution of the velocities of the body is that of translation (this state of motion is also called instantaneous translation). It will be found from Eq. (56) that the angular velocity ω of the body at the given instant is zero.
; the result is the same for all other points of the body. Consequently, in this case the velocities of all points of the body are equal in magnitude and direction at every instant, i.e., the instantaneous distribution of the velocities of the body is that of translation (this state of motion is also called instantaneous translation). It will be found from Eq. (56) that the angular velocity ω of the body at the given instant is zero.
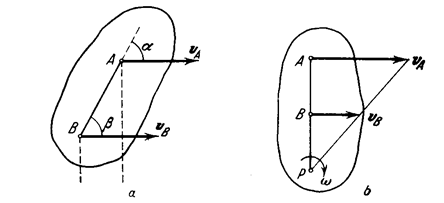
Fig. 24
(c) If the velocities of points A and B are parallel and AB is perpendicular to  , the instantaneous centre of zero velocity P can be located by the construction shown in Fig. 24 b. The validity of this construction follows from the proportion (54). In this case, unlike the previous ones, we have to know the magnitudes of velocities
, the instantaneous centre of zero velocity P can be located by the construction shown in Fig. 24 b. The validity of this construction follows from the proportion (54). In this case, unlike the previous ones, we have to know the magnitudes of velocities 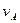 and
and  to locate the instantaneous centre of zero velocity P.
to locate the instantaneous centre of zero velocity P.
(d) If the velocity vector  of a point in section S and the angular velocity ω are known, the position of the instantaneous centre of zero velocity P, lying on the perpendicular to
of a point in section S and the angular velocity ω are known, the position of the instantaneous centre of zero velocity P, lying on the perpendicular to 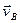 can be immediately found from Eq. (55), which yields
can be immediately found from Eq. (55), which yields 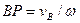 .
.
Comprehension check.
Adjectives
Nouns
Unit 12.
Motion of a Rigid Body Having One Fixed Point.
Learn the following words and word combinations by heart:
| accordingly | соответственно |
| angle of nutation | угол наклона |
| arrow | стрелка |
| attach rigidly | закреплять (подсоединять) жёстко (без шарниров), неподвижно |
| ball-and-socket joint | шарнирное соединение; шаровое соединение |
| be compounded of | состоять из…, быть составленным из |
| by the same reasoning coincide with conclude continuously | по тем же соображениям совпадать с … прийти к заключению, сделать вывод, заключать постоянно, все время |
| describe a curve in space | описывать кривую в пространстве |
| displacement elementary ~ oppositely directed ~ resultant ~ Euler angle | перемещение элементарное, бесконечно малое перемещение (точки) противоположно направленное перемещение результирующее перемещение, смещение эйлеров угол |
| impart | сообщать движение, ускорение; передавать энергию |
| intersect | пересекать; перекрещивать; проходить через (что-л.); |
| hodograph of a vector | годограф вектора |
| kinematics characteristics | кинематические характеристики |
| lie outside line of nodes nutation precession proper rotation | находиться лежать за пределами линия узловых точек; оптическая ось нутация прецессия, прецессионное движение собственное вращение |
| respective point | соответствующая (соответственная) точка |
| same | один и тот же, одинаковый |
| series of consecutive elementary rotations about axis | Ряд последовательных элементарных вращений вокруг оси |
| simultaneously | одновременно |
| spin | вращаться (вокруг своей оси) |
| time rate of change | производная по времени; скорость изменения со временем, ускорение при разгоне или замедлении (рабочего органа) |
| trihedron | триэдр; тройка ортов |
| unlike (the case) | в отличие от (случая) |
| yield | образовывать |
Fig. 25
Line OK, along which planes Oxy and Ox1y1 intersect, is called the line of nodes. The position of the trihedron Oxyz, and hence of the body, with respect to the axes Ox1y1 is given by the angles: j = < KOx, y= < x1OK, q = < z1Oz.
These angles, called the Euler angles, are known by the following names, taken from celestial mechanics: j—the angle of proper rotation, y—angle of precession, q— angle of nutation. The positive directions are shown in Fig. 25 by arrows. A change in angle j indicates a rotation of the body around axis Oz (proper rotation), a change in angle y indicates a rotation around axis 0z1 (precession), and a change in angle q indicates a rotation around the line of nodes OK (nutation).
To describe the body's motion, its position with respect to axes Ox1y1z1 must be known for any instant, i.e.,

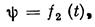
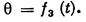
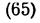
Equations (65) define the law of motion and are called the equations of motion of a rigid body about a fixed point.
To get a full picture of this type of motion, let us demonstrate the following theorem of Euler-d’Alembert: Any elementary displacement of a body having a fixed point represents an elementary rotation about an instantaneous axis of rotation through that point.
Let the body’s position be given by the angles j,y,q. Then its displacement in an elementary time interval dt can be represented as the resultant of a series of rotations through angles dj,dy and dq about axes Oz, Oz1,and OK, respectively. Combined, the three rotations yield the true elementary displacement of the body.
Consider first the resultant displacement of the rotations about axes Oz and Oz1 (Fig. 26). A rotation through angle dj, about axis Oz imparts to any point of the body in the plane zOz 1 (inside angle z0z 1 ) an elementary displacement perpendicular to the plane and equal in magnitude to h1dj, where h1 is the distance of the point from axis Oz. Simultaneously, in the rotation about axis Oz1, the point will receive an oppositely directed displacement of magnitude h2dj. Accordingly, within angle zOz1, there will always be a point B for which
h1dj = h2dy and whose displacement is zero (if the direction of rotation is opposite to that shown in Fig. 26, the point lies outside angle zOz1). Hence we conclude that the body's elementary displacement resulting from the rotations about axes Oz and Oz1 is the same as the displacement of a body with two stationary points 0 and B, i.e., it is an elementary rotation about axis OB through point 0.

Fig. 26
By the same reasoning, the elementary rotations about axes OB and OK are equivalent to an elementary rotation about an axis OP through point 0 (Fig. 26), and the theorem is proved.
Axis OP is called the instantaneous axis of rotation; an elementary rotation of the body about it brings the body into a neighbouring position infinitesimally close to the given position; the velocities of all points of the body lying on the instantaneous axis of rotation are zero. Unlike a fixed axis, the instantaneous axis of rotation continuously changes its direction in space and in the body. The rotation about axis OP, which brought the body into the neighbouring position, is followed by a rotation about the new instantaneous axis of rotation OP1, etc. Thus, the motion of a rigid body about a fixed point is compounded of a series of consecutive elementary rotations about instantaneous axes of rotation through that fixed point (Fig. 26).
Let us examine the kinematics characteristics of this motion.
(1) The angular velocity w with which a body makes an elementary rotation about the instantaneous axis of rotation is called the instantaneous angularvelocity of the body. It can be denoted bya vector w directed along axis OP. As the direction of axis OP changes continuously, vector w changes with time both in magnitude and direction, and its tip A describes a curve AD in space, which is the hodograph of vector w (Fig. 27).

Fig. 27
(2) The instantaneous angular acceleration of a body, which characterizes the time rate of change of the angular velocity w both in magnitude and direction, is a vector quantity
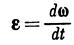
Comparing this expression with the equation v == dr/dt, we conclude that the angular acceleration e can be computed as the velocity with which the tip of vector w moves along curve AD (see Fig. 27). Specifically, the direction of e coincides with the direction of the tangent to curve AD at the respective point. Consequently, unlike the case of rotation about a fixed axis, the direction of vector e does not coincide with that of vector w.
Vectors w and e are the basic kinematic characteristics of the motion of a body having a fixed point. They can be computed when the equations of motion (65) are known.
Comprehension check.
Verbs
Nouns
Verbs
Nouns
Part 3. Free-body diagram.
In the application of any of the force-mass-acceleration equations of motion, it is absolutely necessary to account correctly for all forces acting on the particle. The only forces that we may neglect are those whose magnitudes are negligible compared with other forces acting, such as the forces of mutual attraction between two particles compared with their at-traction to a celestial body such as the earth. The vector sum Σ F of Eq. 1 means the vector sum of all forces acting on the particle in question. Likewise, the corresponding scalar force summation in any one of the component directions means the sum of the components of all forces acting on the particle in that particular direction. The only reliable way to account accurately and consistently for every force is to isolatethe particle under consideration from all contacting and influencing bodies and replace the bodies removed by the forces they exert on the particle isolated. The resulting free-body diagram is the means by which every force, known and unknown, which acts on the particle is represented and hence accounted for. Only after this vital step has been completed should the appropriate equation or equations of motion be written. The free-body diagram serves the same key purpose in dynamics as it does in statics. This purpose is simply to establish a thoroughly reliable method for the correct evaluation of the resultant of all actual forces acting on the particle or body in question. In statics this resultant equals zero, whereas in dynamics it is equated to the product of mass and acceleration. If we recognize that the equations of motion must be interpreted literally and exactly, and if in so doing, we respectthe full scalar and vector meaning of the equals sign in the motion equation, then a minimum of difficulty will be experienced. Every experienced student of engineering mechanics recognizes that careful and consistent observance of the free body method is the most important single lessonto be learned in the study of engineering mechanics. As a part of the drawing of a free-body diagram, the coordinate axes and their positive directions should be clearly indicated. When the equations of motion are written, all force summations should be consistent with the choice of these positive directions.
Adjectives
Nouns
Unit 14.
Work
Learn the following words and word combinations by heart:



