Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ:  Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия ЭкологияТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы расчёта электрических цепей постоянного тока
Метод контурных токов Предполагаем, что в каждом замкнутом контуре схемы течёт свой контурный ток. Число неизвестных токов равно числу независимых контуров. Уравнения для контурных токовсоставляют по второму закону Кирхгофа. Решают полученную систему, после чего определяют токи ветвей через контурные токи. Направления контурных токов можно брать любым.
Рис.1.20
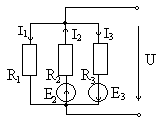
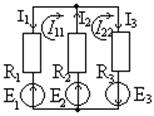
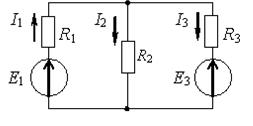
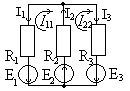
Рассмотрим пример (рис. 1.20). Пусть в первом контуре протекает ток I 11, во втором –ток I 22. Составим для данной схемы систему уравнений для нахождения контурных токов:
Решая систему, найдем контурные токи Выразим искомые токи ветвей через контурные, получим:
Метод эквивалентного генератора
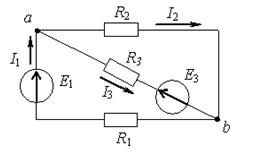
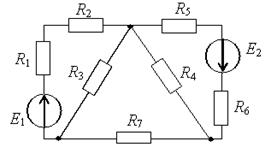
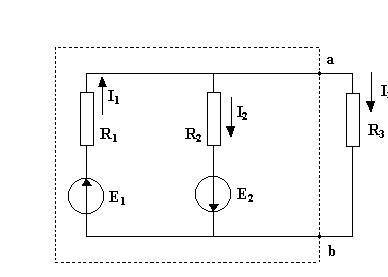
Иногда необходимо исследовать режимы работы одной из ветвей сложной электрической цепи при изменении сопротивления этой ветви. В этом случае целесообразнее воспользоваться методом эквивалентного генератора. По этому методу воздействие всех источников сложной электрической цепи на исследуемую ветвь можно заменить воздействием последовательно соединенной с ветвью эквивалентного генератора, имеющего ЭДС E экв и внутреннее сопротивление R вн. Для расчёта методом эквивалентного генератора необходимо: 1. Разомкнуть ветвь, ток в которой необходимонайти. 2. Любым методом определить разность потенциалов между точками разрыва. Это напряжение называется напряжением холостого хода, обозначается U xxили Е экв. 3. Закоротить все источники ЭДС схемы и определить входное напряжение схемы относительно точек разрыва. Это сопротивление обозначим R экв. 4. Определить ток данной ветви, учитывая её сопротивление по формуле Определим ток I3 методом эквивалентного генератора для схемы, изображенной на рисунке 1.21.
Рис.1.21
Определим Uxx:
Подставим выражение для тока в выражение для напряжения холостого хода, получим:
Определим R экв
Определим ток I 3
Если сопротивление ветви сделать равным нулю, то для неё будет иметь место режим короткого замыкания, а протекающий ток будет током короткого замыкания I3кз.
Отсюда следует определение входного сопротивления схемы; для этого надо измерить напряжение холостого хода на зажимах разомкнутой ветви (U xx) и ток короткого замыкания (I кз) ветви и найти R экв, поэтому, этот метод ещё называют и методом холостого хода (XX) и (короткого замыкания) КЗ.
Метод эквивалентного генератора может быть использован для определения тока в нелинейном элементе разветвленной цепи постоянного тока.
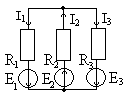
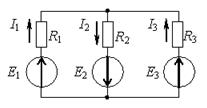
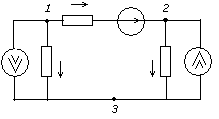
Метод узловых потенциалов Этот метод позволяет уменьшить число совместно решаемых уравнений до У-1, где У – число узлов схемы замещения цепи. Метод основан на применении 1 закона Кирхгофа, и заключается в следующем: 1. один узел цепи принимаем за базовый с нулевым потенциалом. Такое допущение не изменяет значения токов в ветвях, т.к. ток в каждой ветви зависит только от разностей потенциалов узлов, а не от действительных значений потенциалов. 2. Для остальных У-1 узлов составляем уравнения по первому закону Кирхгофа, выражая токи через потенциалы узлов. 3. Решением составленной системы уравнений определяем потенциалы У-1 узлов относительно базового, а затем токи ветвей по обобщенному закону Ома. Рассмотрим применение метода на примере расчета цепи, изображенной на рисунке 1.22, содержащей У =3 узла.
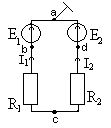
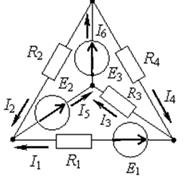
Рис.1.22 Узел 3 принимаем базовым, т.е. Узел 1: Узел 2: Где:
Подставим значения токов в уравнения, составленные для узлов, и выразим их через проводимости, получим:
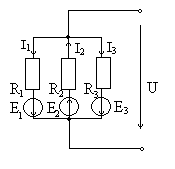
Решение полученной системы методом подстановок, или численным методом с использованием ЭВМ определяет потенциалы узлов Метод двух узлов Метод двух узлов является частным случаем метода узловых потенциалов.Этим методом можно рассчитать сложную электрическую цепь, содержащую 2 узла (рис.1.23).
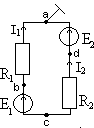
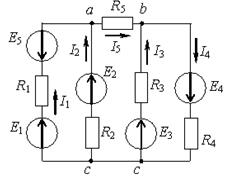
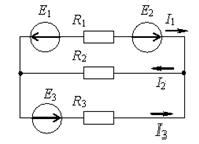
Рис.1.23 Рассмотрим схему, в которой имеется 2 узла и 3 ветви. Напряжение между узлами a и b называется узловым. Выберем условные положительные направления токов и узлового напряжения, тогда, для 1 ветви: 2 ветви: для любой n –й ветви: По первому закону Кирхгофа, для узла A:
Подставляя значения токов, после преобразований получим:
В общем случае формула для определения узлового напряжения
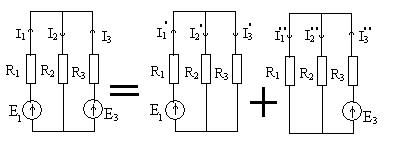
Здесь со знаком (+) записывают ЭДС, направленные встречно узловому напряжению, со знаком (-) – направленные согласно с напряжением Uab.
Метод наложения (суперпозиции).
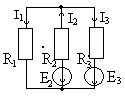
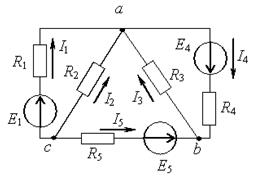
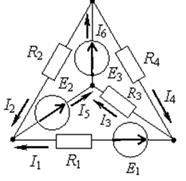
Рис.1.24 Метод основан на независимости действия ЭДС, а именно: протекающие в цепи ЭДС токи можно представить как алгебраическую сумму токов, вызываемых каждой из ЭДС в отдельности. Следовательно, расчет сложной цепи с несколькими ЭДС сводится к расчету нескольких цепей, каждая из которых имеет один источник питания. 1. Поочередно находят в ветвях схемы значения токов и их направления, создаваемые каждой из ЭДС в отдельности, мысленно исключая остальные ЭДС из схемы, но оставляя их внутренние сопротивления (если они заданы). Токи обозначаем 2. Находят действительные токи в ветвях путем алгебраического сложения токов, создаваемых каждой ЭДС. Метод применим только для линейных цепей. Не применим для расчета мощностей, т.к. мощность пропорциональна квадрату тока.
1.2 Задания для практических занятий и самостоятельной работы
ЛАБОРАТОРНАЯ РАБОТА №1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 169; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.121.242 (0.022 с.) |
.
,
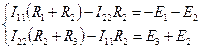
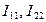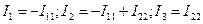
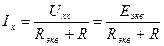
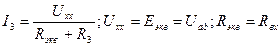
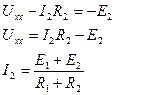
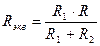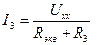
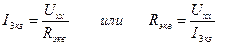
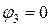. Для узлов 1 и 2 уравнения по первому закону Кирхгофа:
;
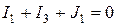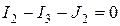
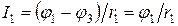
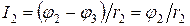
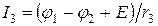
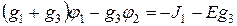
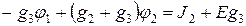
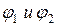, а, следовательно и токи ветвей.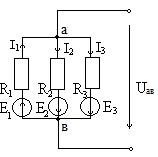
,
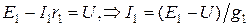
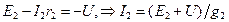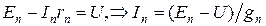
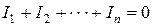
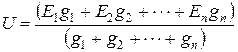
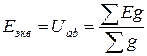
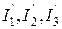для 1 упрощенной схемы, для 2 
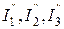и т.д. в зависимости от количества полученных схем.
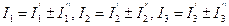и т.д.
