
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление спектра частот собственных колебаний
Для вычисления спектра частот собственных колебаний достаточно рассмотреть уравнение изогнутой оси балки (15.49), подчинив его условиям закрепления ее на опорах. Из этих условий получим систему однородных уравнений, определитель которой приравниваем нулю. Это приведет к трансцендентному уравнению, собственные числа которого дадут возможность найти волновые числа k, а затем на основании (15.48) можно вычислить спектр частот собственных колебаний.
Решение. Используем уравнение изогнутой оси балки (15.49) и дважды его продифференцируем:
Из условий закрепления балки на левой опоре
а согласно (15.48) получаем спектр частот собственных колебаний
При n =1
Это первый тон колебаний с симметричной формой изгиба балки по одной полуволне, рис. 15.14 а. При n =2 возникает второй тон колебаний с кососимметричной формой изгиба, рис.15.14 б:
Бесконечное множество корней трансцендентного уравнения (15.51) определяет спектр частот с соответствующей формой колебаний. Формы колебаний зависят от способа возбуждения собственных колебаний. Можно вызвать только первую форму колебаний, если отклонить балку от положения статического равновесия прогибом посередине пролета. Можно вызвать лишь вторую форму, если отклонить балку одинаковыми перемещениями в симметрично расположенных сечениях в разные стороны от оси. Если придать балке начальный несимметричный изгиб, то возникнут все формы колебаний.
Метод начальных параметров в колебаниях балок
При наличии на балке сосредоточенных масс, а также в балках с несколькими участками, удобно применять метод начальных параметров, избегая стыковки на границах участков
Рассмотрим уравнение (15.49) и его производные:
Выразим постоянные интегрирования через начальные параметры из условий:
Из этих условий получим зависимости:
Отсюда находим:
и подставим в уравнение изогнутой оси (15.50)
Здесь введены функции А.Н. Крылова:
Уравнением (15.52) пользуются так же, как (15.50).
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 150; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.184.237 (0.006 с.) |
 Пример 15.7.Двухопорная балка (рис. 15.13) с равномерно распределенной массой испытывает собственные колебания. Найти спектр частот собственных колебаний.
Пример 15.7.Двухопорная балка (рис. 15.13) с равномерно распределенной массой испытывает собственные колебания. Найти спектр частот собственных колебаний.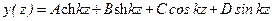 ,
,
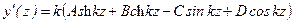
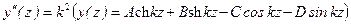
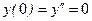 получаем A + C = 0 и A - C =0, откуда находим A + C + 0. Из условий на правой опоре
получаем A + C = 0 и A - C =0, откуда находим A + C + 0. Из условий на правой опоре 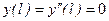 получаем систему уравнений
получаем систему уравнений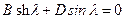 ,
, 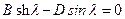 ,
, 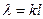 .
.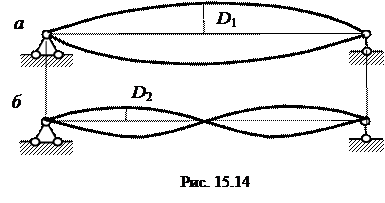 Отсюда следует, что
Отсюда следует, что 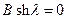 и
и 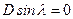 . В первом равенстве
. В первом равенстве 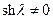 , т.к.
, т.к. 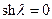 только при λ=0, т.е. при k =0. Но при этом и
только при λ=0, т.е. при k =0. Но при этом и 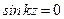 , что соответствует отсутствию перемещений. Значит B =0. Во втором равенстве
, что соответствует отсутствию перемещений. Значит B =0. Во втором равенстве 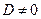 , так как при D =0 не будет колебаний. Значит sin λ=0, т.е. λ= n π, т.е. k = n π / l и уравнение движения сечений принимает вид:
, так как при D =0 не будет колебаний. Значит sin λ=0, т.е. λ= n π, т.е. k = n π / l и уравнение движения сечений принимает вид: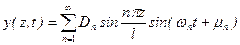 ,
,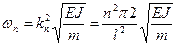 . (15.51)
. (15.51)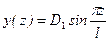 ,
, 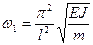 .
.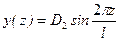 ,
, 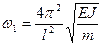 .
.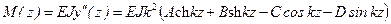
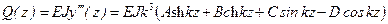
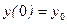 ,
, 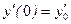 ,
, 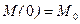 ,
, 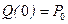 .
.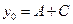 ,
, 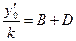 ,
, 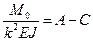 ,
, 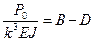 .
.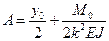 ,
, 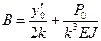 ,
, 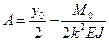 ,
, 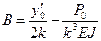
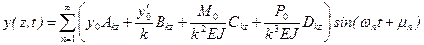 . (15.52)
. (15.52)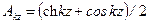 ,
, 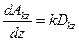 ,
, 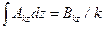 ,
,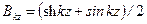 ,
, 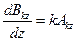 ,
, 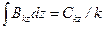 , (15.53)
, (15.53)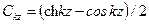 ,
, 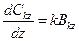 ,
, 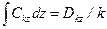 ,
,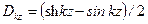 ,
, 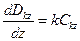 ,
, 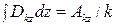 .
.


