
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные незатухающие колебанияСодержание книги
Поиск на нашем сайте Для возбуждения собственных колебаний сообщим сосредоточенной массе некоторую скорость движения или отклоним упругую систему (балку) из положения статического равновесия некоторой нагрузкой, которая затем снимается, и колебания происходят за счет сообщенной системе энергии, непрерывно переходящей из потенциальной в кинетическую и обратно. Уравнение перемещений груза (15.1) будет иметь вид
или
где обозначено Решение однородного уравнения, полученного из (15.2) при g =0, имеет вид
или
Приравнивая (15.3) и (15.4), получим
Частное решение уравнения (15.2) ищем в виде где Тогда полное перемещение массы
Отсюда следует, что колебания происходят относительно положения статического равновесия. Значит, при изучении колебаний статическую нагрузку можно учитывать отдельно от динамической. Выразим амплитуду колебаний С и начальную фазу μ через начальные параметры из условий
Амплитуда – это наибольшее перемещение колеблющейся массы. Начальной фазой называется безразмерный параметр, определяющий начальное перемещений массы при колебаниях. Следовательно: амплитуда, т.е. наибольшее перемещение колеблющейся массы:
а начальная фаза, т.е. безразмерный параметр, определяющий начальное перемещений массы при колебаниях
Циклическая частота колебанийи период колебанийопределяются формулами:
Отсюда следует
После определения перемещений y (t) можно найти силу инерции колеблющейся массы Аналогичные расчетные формулы будут при продольных колебаниях невесомого стержня с площадью поперечного сечения F при наличии сосредоточенной массы М. Обозначив продольные перемещения груза Q = Mg через u (t), получим:
При крутильных колебаниях невесомого вала с диском, момент инерции которого относительно оси вращения задан
(здесь: Δ – толщина диска, γ – плотность материала,
Пример 15.1.На невесомом канате со скоростью υ опускается груз Q = Mg, рис. 15.4. Найти расчетное напряжение в канате при внезапном защемлении его верхнего сечения, если длина каната l и его жесткость EF заданы. Решение. После защемления каната возникают собственные колебания, вызванные воздействием начальной скорости движения массы. Так как начального перемещения нет u 0 =0, то согласно (15.10) амплитуда Сила инерции колеблющейся массы С учетом статического нагружения расчетное усилие в канате
Следовательно, для определения динамического коэффициента k д нужно вычислить удлинение каната от статического воздействия груза Q. Расчетное напряжение σ= N / F.
Пример 15.2.Невесомый вал диаметром d и длиною l с диском массой М, диаметром D и толщиною Δ равномерно вращается с угловой скорость
где Уравнение угловых колебательных перемещений диска Отсюда можно найти крутящий момент сил инерции диска
и напряжение
Решение. Удар неупругой массы М вызывает собственные колебания воздействием скорости v. Согласно (15.7) - (15.9) получаем: Уравнение динамических перемещений масс
Отсюда можно найти силу инерции движущихся масс
Амплитудное значение силы инерции
Решение. В этом примере колебания вызваны отклонением груза из положения статического равновесия, показанного на рис. 15.7 горизонтальной (недеформированной) осью, перемещением y 0 =Δ1p.. Так как v 0=0, то согласно (15.7) - (15.9) получаем μ=∞ и уравнение движения массы принимает вид
Единичные перемещения вычисляем по правилу Верещагина перемножением эпюр, показанных на рис. 15.7:
Амплитудное значение силы инерции
По силе находится расчетный изгибающий момент
Обращаем внимание на то, что динамическое воздействие на балку не зависит от массы М, но масса влияет на частоту колебаний.
|
||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 237; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


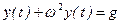 , (15.2)
, (15.2)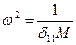 .
.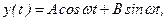 (15.3),
(15.3), . (15.4)
. (15.4)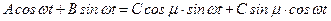 , откуда находим, что
, откуда находим, что 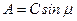 ,
, 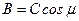 . Отсюда получаем формулы перехода решения (15.3) в (15.4) и наоборот:
. Отсюда получаем формулы перехода решения (15.3) в (15.4) и наоборот: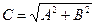 ,
,  . (15.5)
. (15.5) , подставляя которое в (15.2), получим
, подставляя которое в (15.2), получим  , т.е.,
, т.е., 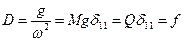 ,
, - статический прогиб балки m в месте приложения груза.
- статический прогиб балки m в месте приложения груза.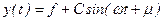 . (15.6)
. (15.6)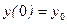 ,
, 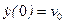 на основании уравнений:
на основании уравнений: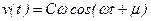 , оттуда получим:
, оттуда получим: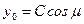 ,
, 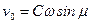 .
.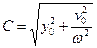 , (15.7)
, (15.7) . (15.8)
. (15.8)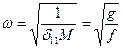 ,
, 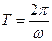 . (15.9)
. (15.9)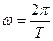 , т.е. циклическая или круговая частота ω представляет количество колебаний за 2π секунд, а период колебаний
, т.е. циклическая или круговая частота ω представляет количество колебаний за 2π секунд, а период колебаний 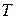 - это время, через которое параметры колебательного процесса (перемещения, силовые факторы) повторяются. Период и частота связаны обратной зависимостью
- это время, через которое параметры колебательного процесса (перемещения, силовые факторы) повторяются. Период и частота связаны обратной зависимостью .
.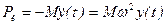 , на которую следует рассчитывать заданную систему.
, на которую следует рассчитывать заданную систему.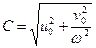 ,
, 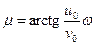 ,
,  . (15.10)
. (15.10) , (15.11)
, (15.11)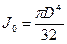 - полярный момент инерции площади поперечного сечения диска) расчетные формулы (15.10) принимают вид:
- полярный момент инерции площади поперечного сечения диска) расчетные формулы (15.10) принимают вид: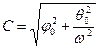 ,
, 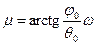 ,
, 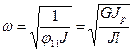 . (15.12)
. (15.12)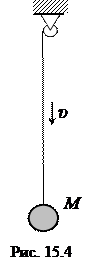 Здесь: φ0 - начальный угол закручивания вала в месте закрепления диска, θ0 - начальная угловая скорость вращения вала,
Здесь: φ0 - начальный угол закручивания вала в месте закрепления диска, θ0 - начальная угловая скорость вращения вала, 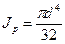 - полярный момент инерции площади поперечного сечения вала диаметра d.
- полярный момент инерции площади поперечного сечения вала диаметра d. , начальная фаза μ=0, частота колебаний
, начальная фаза μ=0, частота колебаний  и уравнение движения груза
и уравнение движения груза 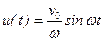 .
.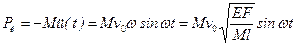 .
. .
.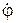 и внезапно тормозится на левом торце, рис.15.5. Найти расчетное напряжение.
и внезапно тормозится на левом торце, рис.15.5. Найти расчетное напряжение.
 Решение. Так как колебания вызваны угловой скоростью
Решение. Так как колебания вызваны угловой скоростью 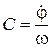 ,
, 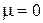 ,
,  ,
,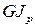 крутильная жесткость вала с полярным моментом инерции площади поперечного сечения
крутильная жесткость вала с полярным моментом инерции площади поперечного сечения  ,
,  - момент инерции массы диска относительно оси вращения (см. (15.11))
- момент инерции массы диска относительно оси вращения (см. (15.11))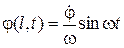 .
.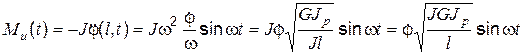
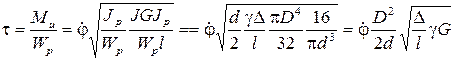 .
. Пример 15.3.На невесомую консоль с сосредоточенной массой М 0 со скоростью v налетает неупругая масса М, вызывая совместные колебания этих масс, рис.15.6. Найти расчетные изгибные напряжения. Геометрические характеристики консоли l, F, W заданы.
Пример 15.3.На невесомую консоль с сосредоточенной массой М 0 со скоростью v налетает неупругая масса М, вызывая совместные колебания этих масс, рис.15.6. Найти расчетные изгибные напряжения. Геометрические характеристики консоли l, F, W заданы.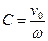 , μ=0, где
, μ=0, где 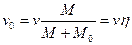 начальная скорость совместного движения масс, η – коэффициент передачи энергии.
начальная скорость совместного движения масс, η – коэффициент передачи энергии. .
.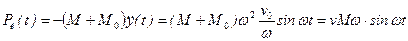 .
.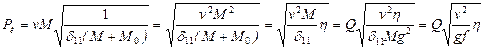 (15.13) в защемлении создает изгибающий момент
(15.13) в защемлении создает изгибающий момент  с напряжением
с напряжением 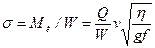 ,
, 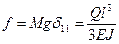 - квазистатический прогиб консоли от веса Q.
- квазистатический прогиб консоли от веса Q.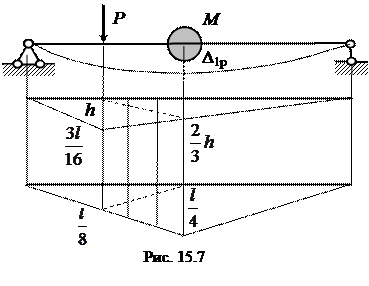 Пример 15.4.Двухопорная невесомая балкас сосредоточенной массой М посередине пролета отклонена от положения статического равновесия силой Р, которая затем внезапно снимается, рис. 15.7. Вычислить расчетный динамический изгибающий момент.
Пример 15.4.Двухопорная невесомая балкас сосредоточенной массой М посередине пролета отклонена от положения статического равновесия силой Р, которая затем внезапно снимается, рис. 15.7. Вычислить расчетный динамический изгибающий момент.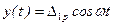 . Сила инерции колеблющейся массы
. Сила инерции колеблющейся массы .
. ,
,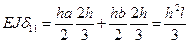 .
.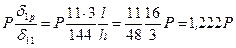 .
.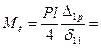 0,305 Pl.
0,305 Pl.


