
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные случаи напряженного состояния оболочек
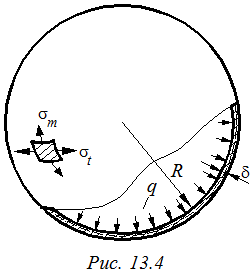
а) Сферический сосуд под действием равномерного внутреннего давления q (рис.13.4).
Собственным весом стенок сосуда и газа пренебрегаем. Для такого сосуда радиусы кривизны в меридиональном и окружном направлении одинаковы ρ m = ρ t = R.
Учитывая симметрию оболочки можно записать σ m = σ t = σ Полагая в формуле (13.2) p = q получим
б) Цилиндрический сосуд под действием равномерного внутреннего давления p = q (рис. 13.5).
Рис. 13.5
Для цилиндра образующие являются меридианами, следовательно, ρ m = ∞. В кольцевом направлении ρ t = R. После подстановки указанных радиусов кривизны в формулу (13.2) получим Меридиональные напряжения найдем из выражения (13.4.), полагая α = 0 и Q = 0
Анализ формул (13.7) и (13.8) показывает, что в цилиндрическом сосуде кольцевые растягивающие напряжения в два раза больше меридиональных растягивающих напряжений. Напряжение в сферическом днище резервуара можно вычислить по формуле (13.8), приняв значение R = R д.
в) Вертикальный резервуар с коническим днищем под действием веса жидкости. Широкое распространение в практике строительства получили вертикальные цилиндрические резервуары для хранения сыпучих и жидких материалов. Учитывая, что разгрузка материалов производится снизу, днище таких резервуаров делается коническим с отверстием (рис. 13.6).
Рис.13.6 Радиус кривизны меридиональных сечений цилиндрической части резервуара ρ m = ∞. Следовательно, из уравнения (13.2) следует На произвольной глубине, равной (H + h - z)давление равно p = γ (H + h - z) (а)
Для конической части резервуара можно записать
Подставляя выражения (а) и (в) в формулу (13.9) найдем значение окружного напряжения в конической части резервуара
Для цилиндрической части резервуара, полагая ρ t = R, найдем Эпюра σ t показана на (рис.13.6) слева. Меридиональные напряжения найдем из следующих соображений. Вес жидкости в конической части резервуара равен
Подставляя выражение (с) в формулу (13.4) получим
Эпюра σ m показана на (рис.13.6) справа. Меридиональные напряжения в цилиндрической части сосуда по высоте постоянны. Напряжения, возникающие на стыке цилиндрической и конической части сосуда найдем, полагая в формуле (13.12) z = h, cos α = 1.
В местах примыкания цилиндрической и конической части резервуара возникают радиальные составляющие меридиональных напряжений, равные σ m sinα (рис. 13.7). Эти неуравновешенные составляющие по периметру кольца создают радиальную нагрузку, равную q = δ σ m sin α
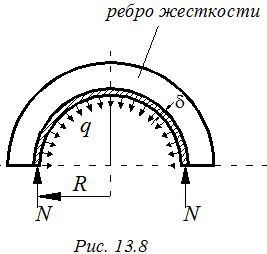
Эта нагрузка стремится согнуть концы цилиндрической оболочки вовнутрь. Для восприятия этой радиальной нагрузки по периметру цилиндра ставится ребро жесткости из уголка или швеллера (рис. 13. 8). Проектируя все силы на вертикаль, получим, что величина сжимающей силы кольца равна N = qR
Установка ребра жесткости не устраняет изгиб стенок сосуда, так как ребро жесткости препятствует расширению кольца оболочки, примыкающему к нему. Оболочка вблизи кольца жесткости искривляется. Это явление носит название краевого эффекта. Краевой эффект приводит к появлению местных напряжений в стенке оболочки. Краевой эффект подробно рассматривается в моментной теории расчета оболочек.
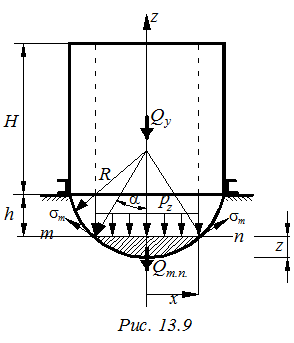
Пример №13.1. Цилиндрический резервуар радиусом r со сферическим днищем заполнен жидкостью, плотность которой равнa γ (рис. 13.9) Радиус сферы равен R, толщина днища δ. Давление жидкости на произвольной высоте цилиндра с координатой z равно pz = γ (H + h – z)
Н – высота цилиндрической части резервуара, h - высота сферической части резервуара.
Согласно формуле (13.7) кольцевые напряжения в цилиндрической части резервуара можно найти как
Рассматривая равновесие нижней части сферического резервуара, запишем S Fz =0 σ m F к sin α – Q ц – Q ш.с =0 13.14 Q ц – вес жидкости выше сечения mn, заполняемый объем цилиндрической формы
Q ц = F ц h ц γ = π x 2 (H + h - z)γ (d) Q ш.с. –вес жидкости, заполняемой объем шарового сегмента
Q ш.с = γ V = γπ z 2 (3 R – z) (e)
После подстановки (d) и (е) в уравнение (13.14) находим σ m δ2π x sin α - π x 2(H + h – z)γ – γπ z 2 (3 R – z) = 0 Учитывая, что x 2 = R 2 – (R – z)2 = z (2 R – z) после подстановки в предыдущее уравнение получим Из формулы Лапласа (13.2) найдем При z = 0
В том случае, когда днище выполнено в виде полусферы, (при z=0)
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.42.196 (0.009 с.) |
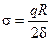 13.6
13.6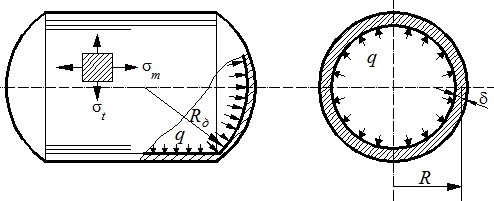
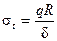 13.7
13.7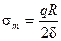 13.8
13.8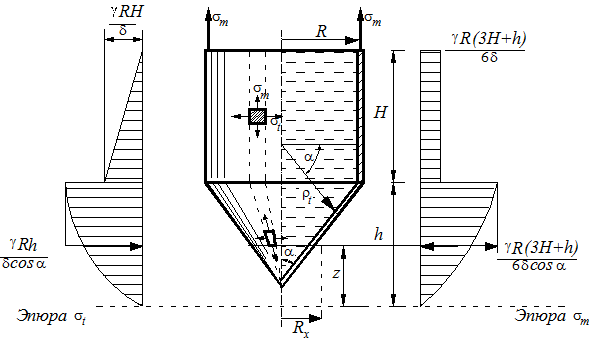
 13.9
13.9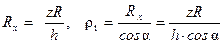 (в)
(в)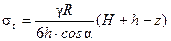 13.10
13.10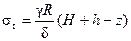 13.11
13.11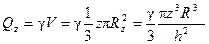 (c)
(c)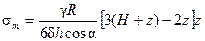 13.12
13.12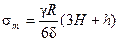 13.13
13.13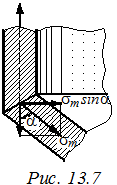

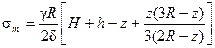 13.5
13.5 13.6
13.6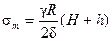

 .
.


