
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вынужденные колебания при гармонических нагрузках
В случае гармонических нагрузок Нужно найти решение уравнения (15.1)
которое приводит к неоднородному дифференциальному уравнению
где обозначено Так как
Частное решение этого уравнения ищем в виде
Отсюда находим:
Обозначив
Так находим частное решение неоднородного уравнения (15.33)
Обозначим:
откуда
При таких обозначениях уравнение движения массы примет следующий вид
где ν – коэффициент нарастания колебаний, а ρ – начальная фаза. В случае сосредоточенной возмущающей силы
где k д – динамический коэффициент при вынужденных колебаниях от гармонической нагрузки. Заметим, что до резонанса, когда θ<ω, т.е. δ<1, сдвиг фазы вынужденных колебаний (15.34) отрицательный, т.е. отставание движение груза происходит против направления возмущающей нагрузки. При резонансе, когда δ=1 и
Однако, вдали от резонанса при 0,7 > δ > 1,3 можно пользоваться формулой (15.38). При δ>1 динамический коэффициент уменьшается и при δ, устремляющемся к бесконечности, коэффициент нарастания колебаний ν падает до нуля, т.е. динамический эффект при таких высоких частотах возмущения проявляться не будет. Без учета сопротивления движению уравнение перемещения массы значительно упрощается. В этом случае в дифференциальное уравнение (15.21)
Тогда частное решение будет иметь вид
Найти расчетный изгибающий момент Грузовой коэффициент
Дифференцированием получаем уравнение углов поворота
Из условий защемления консоли, Отсюда при a =0 получаем перемещение от единичной силы Коэффициент нарастания колебаний По формуле 15.39 получаем динамическое перемещение массы в установившемся режиме колебаний
Сила инерции колеблющейся массы
Амплитудное значение изгибающего момента в защемлении
|
|||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 69; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.79.59 (0.006 с.) |
 , т.е. нагрузки, изменяющейся по закону синуса (или косинуса) нужно вычислять интеграл (15.25). Но этого можно избежать следующим путем.
, т.е. нагрузки, изменяющейся по закону синуса (или косинуса) нужно вычислять интеграл (15.25). Но этого можно избежать следующим путем.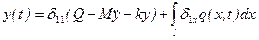 ,
,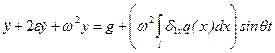 , (15.32)
, (15.32)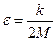 .
. представляет статическое перемещение массы М от амплитудного воздействия возмущающей нагрузки, а
представляет статическое перемещение массы М от амплитудного воздействия возмущающей нагрузки, а 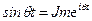 , то уравнение (15.32) представим в виде
, то уравнение (15.32) представим в виде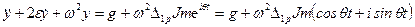 . (15.33)
. (15.33) и подставим в дифференциальное уравнение
и подставим в дифференциальное уравнение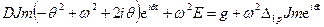 .
.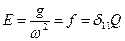 ,
,  ,
, 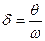 .
. (логарифмический декремент затухания) и
(логарифмический декремент затухания) и  (период собственных незатухающих колебаний), получим амплитуду колебаний
(период собственных незатухающих колебаний), получим амплитуду колебаний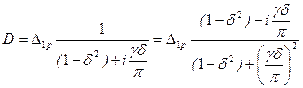 .
.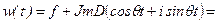
 .
.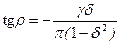 , (15.34)
, (15.34)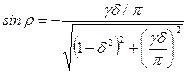 ,
, 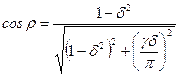 ,
,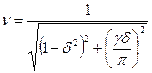 . (15.35)
. (15.35) , (15.36)
, (15.36)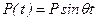 , подставляя в (15.36) значения перемещений
, подставляя в (15.36) значения перемещений 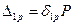 и
и  , получим амплитудное перемещение массы
, получим амплитудное перемещение массы , (15.37)
, (15.37)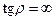 , получим
, получим 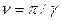 , т.е. коэффициент нарастания колебаний не бесконечно большой, как это следует из приближенного значения ν, пренебрегая затуханием колебаний
, т.е. коэффициент нарастания колебаний не бесконечно большой, как это следует из приближенного значения ν, пренебрегая затуханием колебаний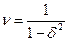 . (15.38)
. (15.38)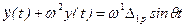 нужно подставить частное решение
нужно подставить частное решение  , в результате чего получим
, в результате чего получим  , откуда найдем амплитуду
, откуда найдем амплитуду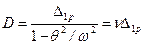 .
.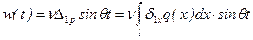 . (15.39)
. (15.39) Пример 15.6.Невесомая балка с сосредоточенной массой М испытывает воздействие гармонической возмущающей силы
Пример 15.6.Невесомая балка с сосредоточенной массой М испытывает воздействие гармонической возмущающей силы 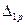 , т.е. квазистатическое перемещение в точке приложения массы от амплитудного значения возмущающей силы можно вычислить методом начальных параметров из уравнения изогнутой оси балки
, т.е. квазистатическое перемещение в точке приложения массы от амплитудного значения возмущающей силы можно вычислить методом начальных параметров из уравнения изогнутой оси балки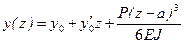 .
.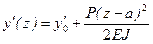 .
.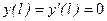 , находим начальные параметры:
, находим начальные параметры: 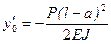 ,
, 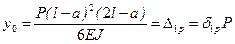 .
.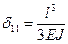 . Частота собственных колебаний
. Частота собственных колебаний 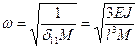 .
.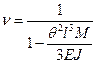 .
. .
.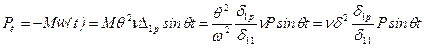 .
.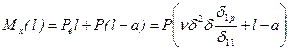 .
.


