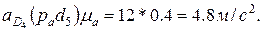Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
И подставим его в первое уравнение, с учетом формулы (2.4) получим значениеСодержание книги
Поиск на нашем сайте
При вторичном дифференцировании уравнений (2.3) с использованием понятия аналога углового ускорения, представляющего вторую производную по углу поворота ведущего звена
Из уравнения (2.19) получим значение Получив значения угловых скоростей и ускорений, можно определить скорость и ускорение любой точки звеньев механизма. В тех случаях, когда
Раскладывая в ряд радикал, входящий в формулу (2.20) по биному Ньютона и ограничиваясь его первыми двумя членами, получим
После дифференцирования скорость Vc и ускорение
Пример. Построить план скоростей и ускорений механизма поперечно-строгального станка (рис. 2. 6,а), у которого В результате структурного анализа устанавливаем в механизме наличие группы пятого вида — звенья 4 (ползун) и 5 (резцовая головка), образующие кинематические пары D4, Е (внешние), D5 (внутреннюю), и третьего вида — звенья 2 (ползун) и 3 (кулиса), образующие кинематические пары В2, С (внешние), В3 (внутреннюю). Для отыскания скоростей звеньев 2 и 3 определяем скорость общей точки на этих двух звеньях, совпадающей с центром вращательной пары. Такой точкой будет точка В3 на звене 3, совпадающая в данный момент с точкой В2. Скорость точки В2 , являющейся общей для ведущего звена (палец кривошипа) и звена 2 (внешняя пара), определяем из условия Скорость точки С, принадлежащей стойке, равна нулю. Скорость точки В3 звена 3 определим через известные скорости точек звеньев, примыкающих к звену 3, — точки В2 на звене 2 и точки С на звене 0: Выбираем масштаб плана скоростей
Угловая скорость
Рис. Кинематический анализ механизма поперечно-строгального станка Скорость центра вращательной пары D4, являющейся внешней для группы 4 —5, равна скорости точки D3 звена 3. Из подобия плана относительных скоростей плану звена
Скорость точки Do на стойке равна нулю;
Через точки d4 и d0 плана скоростей проводим линию действия скорости
На основании аналогичных рассуждений строится план ускорений механизма. Векторные уравнения для определения ускорения точки В3 имеют вид
Ускорение точки В2 как совпадающей с точкой В1 пальца кривошипа
Откладываем в выбранном масштабе Величины нормального ускорения
Эти ускорения в виде соответствующих отрезков
Угловое ускорение третьего звена по формуле, аналогичной формуле (2.13), Из подобия плана относительных ускорений плану звена определим ускорение
и в масштабе Для определения ускорения
Кориолисовы ускорения На пересечении указанных линий определится положение точки d5, и, следовательно, полное ускорение
|
||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 79; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.121 (0.008 с.) |

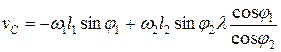 =
= 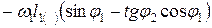 . (2.18)
. (2.18)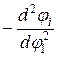 , можно определить действительное ускорение i -ro звена, умножив аналог углового ускорения на квадрат угловой скорости ведущего звена
, можно определить действительное ускорение i -ro звена, умножив аналог углового ускорения на квадрат угловой скорости ведущего звена 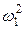 . При этом принимая, что
. При этом принимая, что 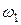 = const, получают уравнения для определения углового ускорения шатуна ε2 и относительного ускорения звена
= const, получают уравнения для определения углового ускорения шатуна ε2 и относительного ускорения звена 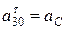 :
: (2.19)
(2.19)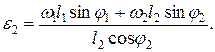
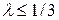 , пользуются приближенными формулами при определении перемещения, скорости и ускорения ползуна. При этом перемещение ползуна Sс измеряем от мертвого положения Со (рис. 2.2): Sc =
, пользуются приближенными формулами при определении перемещения, скорости и ускорения ползуна. При этом перемещение ползуна Sс измеряем от мертвого положения Со (рис. 2.2): Sc = 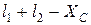 , или с учетом (2.5) получим
, или с учетом (2.5) получим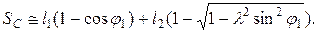 (2.20)
(2.20)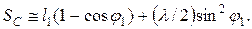 (2.21)
(2.21) определяют по формулам:
определяют по формулам: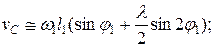 (2.22)
(2.22)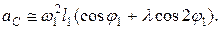 (2.24)
(2.24) = 0,1 м; lCD = 0,3 м; lАС = 0,125 м при
= 0,1 м; lCD = 0,3 м; lАС = 0,125 м при 
 ;
; 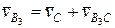 .. D4
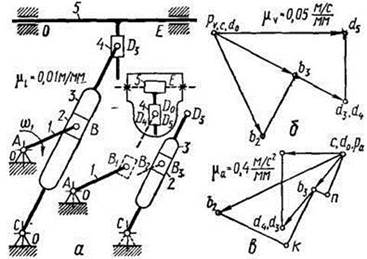
.. D4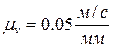 . Скорость
. Скорость 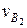 откладываем от полюса
откладываем от полюса 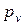 (рис.2.6, б) в виде отрезка pvb2 = 1/0,05 = 20 мм, перпендикулярного к кривошипу 1. Скорость vс = 0 определяется точкой, совпадающей с полюсом рv. Через точки b2 и с проводим соответственно линии действия скоростей
(рис.2.6, б) в виде отрезка pvb2 = 1/0,05 = 20 мм, перпендикулярного к кривошипу 1. Скорость vс = 0 определяется точкой, совпадающей с полюсом рv. Через точки b2 и с проводим соответственно линии действия скоростей 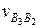 — параллельно звену 3 (кулисе) и
— параллельно звену 3 (кулисе) и 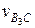 — перпендикулярно к кулисе. Пересечение линий действия скоростей
— перпендикулярно к кулисе. Пересечение линий действия скоростей 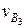 и относительных
и относительных 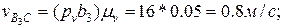
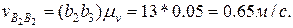
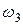 кулисы согласно формуле (2.8)
кулисы согласно формуле (2.8)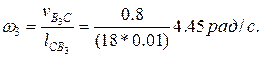
 Определяем скорости звеньев группы пятого вида. Аналогично предыдущему выбираем на звене точку D5, совпадающую с центром вращательной пары D4. Скорость точки D5 определим через известные скорости точек звеньев, примыкающих к звену 5: точки D4 на звене 4 и Do на звене 0.
Определяем скорости звеньев группы пятого вида. Аналогично предыдущему выбираем на звене точку D5, совпадающую с центром вращательной пары D4. Скорость точки D5 определим через известные скорости точек звеньев, примыкающих к звену 5: точки D4 на звене 4 и Do на звене 0.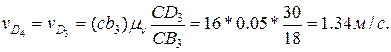
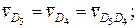
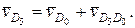
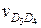 параллельно направляющей поступательной пары 4 — 5 и
параллельно направляющей поступательной пары 4 — 5 и 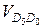 — параллельно направляющей поступательной пары 5 — 6 до их пересечения в точке D5. Абсолютная скорость точки D5
— параллельно направляющей поступательной пары 5 — 6 до их пересечения в точке D5. Абсолютная скорость точки D5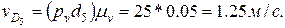
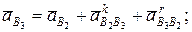
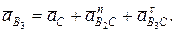

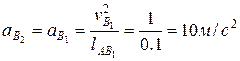 /
/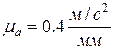 параллельно кривошипу 1 в направлении от точки В1 до А (рис. 2.6, b) в виде отрезка
параллельно кривошипу 1 в направлении от точки В1 до А (рис. 2.6, b) в виде отрезка 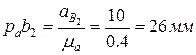 . Ускорение точки С ac = 0, следовательно, точка с б удет находиться в полюсе плана ускорений рa.
. Ускорение точки С ac = 0, следовательно, точка с б удет находиться в полюсе плана ускорений рa.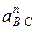 и кориолисова
и кориолисова 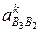 определим по формулам, аналогичным формулам (2.11) и (2.12), пользуясь планом скоростей (рис. 2.6, б):
определим по формулам, аналогичным формулам (2.11) и (2.12), пользуясь планом скоростей (рис. 2.6, б):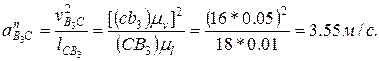
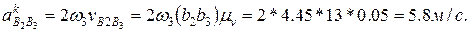
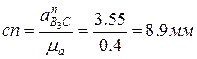 и
и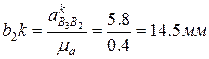 откладываем на плане ускорений: первый от точки с параллельно звену 3 в направлении от точки В3 к точке С; направление второго отрезка определится поворотом вектора относительной скорости
откладываем на плане ускорений: первый от точки с параллельно звену 3 в направлении от точки В3 к точке С; направление второго отрезка определится поворотом вектора относительной скорости 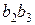 вокруг своего начала (точки b2) в сторону направления вращения кулисы 3 (среды переноса). Через точки п и k проводим перпендикулярно к отрезкам сп и b2k линии действия ускорения
вокруг своего начала (точки b2) в сторону направления вращения кулисы 3 (среды переноса). Через точки п и k проводим перпендикулярно к отрезкам сп и b2k линии действия ускорения 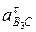 и
и 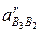 .Пересечение этих линий даст точку b3, определяющую конец вектора ускорения точки
.Пересечение этих линий даст точку b3, определяющую конец вектора ускорения точки 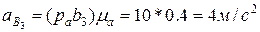 .
.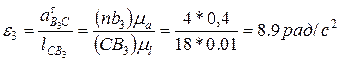 . Направление его можно установить, как указано ранее.
. Направление его можно установить, как указано ранее.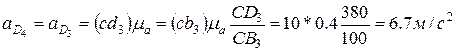
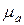 откладываем его в виде отрезка
откладываем его в виде отрезка 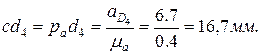
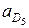 точки D5 составим векторные уравнения:
точки D5 составим векторные уравнения: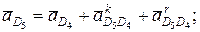
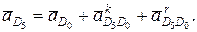
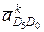 и
и 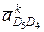 равны нулю вследствие того, что угловые скорости среды переноса w5 и w0 равны нулю. Поэтому через точки d4 и d0 (находящиеся в полюсе ра) проводим линии действия относительных ускорений
равны нулю вследствие того, что угловые скорости среды переноса w5 и w0 равны нулю. Поэтому через точки d4 и d0 (находящиеся в полюсе ра) проводим линии действия относительных ускорений 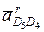 и
и 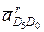 параллельно направляющим поступательных пар, образованных звеньями 4 — 5 и 5 — 0 соответственно.
параллельно направляющим поступательных пар, образованных звеньями 4 — 5 и 5 — 0 соответственно.